高一数学必修三算法初步知识总结高考真题讲练 23页

第十一章 算法初步与框图 一、知识网络 算法初步 算法与程序框图 算法语句 算法案例 算法概念 框图的逻辑结构 输入语句 赋值语句 循环语句 条件语句 输出语句 顺序结构 循环结构 条件结构 二、考纲要求 ‎1.程序框图 ‎　　（1）了解算法的含义，了解算法的思想.‎ ‎　　（2）理解程序框图的三种基本逻辑结构：顺序、条件分支、循环.‎ ‎2.基本算法语句 理解几种基本算法语句――输入语句、输出语句、赋值语句、条件语句、循环语句的含义.‎ 三、复习指南 ‎ 本章是新增内容，多以选择题或填空题形式考查，常与数列、函数等知识联系密切.考查的重点是算法语句与程序框图,以基础知识为主,如给出程序框图或算法语句,求输出结果或说明算法的功能;或写出程序框图的算法语句,判断框内的填空等考查题型.难度层次属中偏低.‎ 第一节 算法与程序框图 ‎※知识回顾 ‎1．算法的概念：算法通常是指按一定规则解决某一类问题的明确和有限的步骤．‎ ‎2.程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形.‎ ‎3.程序框图的三种基本逻辑结构是顺序结构、条件结构、循环结构．‎ ‎4.算法的描述方式有：自然语言、程序框图、程序语言．‎ ‎5.算法的基本特征：①明确性：算法的每一步执行什么是明确的；②顺序性：算法的“前一步”是“后一步”的前提， “后一步”是“前一步”的继续；③有限性：算法必须在有限步内完成任务，不能无限制的持续进行；④通用性：算法应能解决某一类问题.试题提供：www.0839bx.cn ‎※典例精析 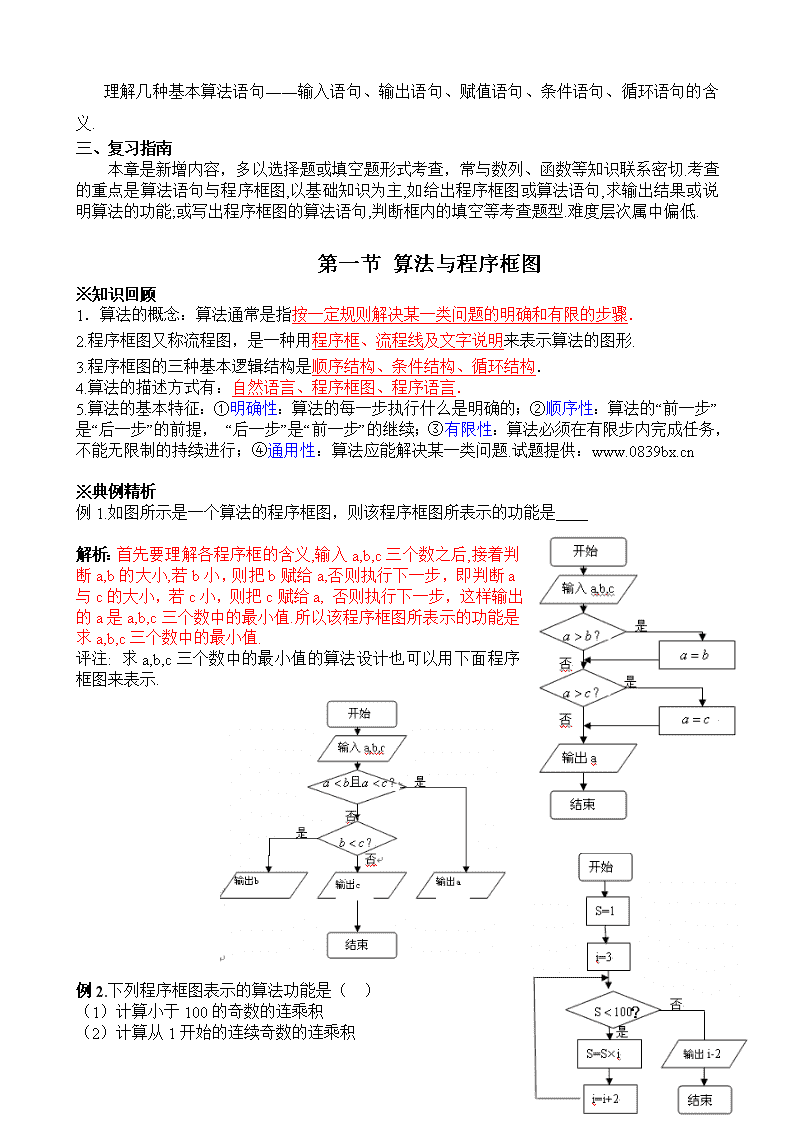例1.如图所示是一个算法的程序框图，则该程序框图所表示的功能是 ‎ 解析：首先要理解各程序框的含义,输入a,b,c三个数之后,接着判断a,b的大小,若b小，则把b赋给a,否则执行下一步，即判断a与c的大小，若c小，则把c赋给a, 否则执行下一步，这样输出的a是a,b,c三个数中的最小值.所以该程序框图所表示的功能是求a,b,c三个数中的最小值.‎ 评注: 求a,b,c三个数中的最小值的算法设计也可以用下面程序框图来表示.‎ 例2.下列程序框图表示的算法功能是（ ） ‎ ‎（1）计算小于100的奇数的连乘积 ‎（2）计算从1开始的连续奇数的连乘积 ‎（3）计算从1开始的连续奇数的连乘积，‎ ‎     当乘积大于100时，计算奇数的个数 ‎（4）计算成立时的最小值 解析：为了正确地理解程序框图表示的算法，可以将执行过程分解，分析每一步执行的结果.可以看出程序框图中含有当型的循环结构,故分析每一次循环的情况,列表如下:‎ 第一次:；‎ 第二次:；‎ 第三次:,此时不成立,输出结果是7,程序框图表示的算法功能是求使成立时的最小值. 选D. ‎ 评注:通过列表,我们能清楚了解程序的每一步中的各个变量是怎样变化的,这正是程序运行的本质所在.本题若要求编写求使成立时的最小值的程序框图或程序时,很容易弄错输出的结果，应注意.‎ 例3.在音乐唱片超市里，每张唱片售价为25元，顾客如果购买5张以上（含5张）唱片，则按九折收费，如果购买10张以上（含10张）唱片，则按八折收费，请设计算法步骤并画出程序框图，要求输入张数x，输出实际收费y(元).‎ 分析:先写出与之间的函数关系式，有，再利用条件结构画程序框图．‎ 解： 算法步骤如下: ‎ 第一步，输入购买的张数,‎ 第二步，判断是否小于5，若是，计算；‎ ‎      否则，判断是否小于10，若是，计算；否则，计算.‎ 第三步，输出.‎ ‎ 程序框图如下:‎ 否 是 输出X 否 评注:凡必须先根据条件做出判断，然后再决定进行哪一个步骤的问题，在画程序框图时，必须引入判断框，采用条件结构设计算法.如果变量分三级(或以上)时,就需要用到条件结构的嵌套,不能忽视结果中“是”、“否”的书写，否则不知道执行哪一条路径.一般地,分段的分段函数,需要引入个判断框.条件结构有以下两种基本类型.‎ 例4.画出求的值的程序框图.‎ 分析:这是一个有规律的数列求和问题,每次都进行了相同的运算,故应用循环结构进行算法设计.‎ 解:程序框图如下:‎ ‎(1)当型循环                        (2)直到型循环 评注: (1) 解题关键是选择好计数变量和累加变量的初始值,并写出用表示的数列的通项公式是 ；‎ ‎(2)循环结构主要用在一些有规律的重复计算的算法中,如累加求和,累乘求积等问题.在循环结构中,要注意根据条件,设计合理的计数变量、累加(积)变量以及它们的初始值等,特别要注意循环结构中条件的表述要恰当、精确，以免出现多一次或少一次循环.‎ ‎（3）循环结构分为两类：一类是当型循环结构，如下左图所示；另一类是直到型循环结构，如下右图所示. ‎ 变式训练画出求的值的程序框图.‎ 解：程序框图如下:‎ 例5.某工厂2005年的生产总值为200万元，技术改进后预计以后后每年的年生产总值都比上一年增长5%.设计一个程序框图，输出预期年生产总值超过300万元的最早年份及2005年到此年份之前(不包此年份)的年生产总值的和.‎ 分析:本例可用循环结构来实现. (1) 确定“循环体”:设a为某年的年生产总值,n为年份,S为年产值的总和,则循环体为 ‎ ‎     ‎ ‎(2)初始化变量:n的初始值为2005,a的初始值为200,S的初始值为0.‎ ‎(3)设定循环控制条件:‎ 解: 程序框图如下:‎ 评注:本问题的关健是设计好循环体,注意与之间的对应关系.本题若将放在之后,则输出时须重新赋值，否则的值为超过300万的年份的下一年.本题也可用当型循环结构来表示.‎ 变式训练：设计一个程序框图，求使的最小的值，并输出此时的值.‎ 解：程序框图如下：‎ ‎※基础自测 一、选择题 ‎1．下列说法正确的是（ ）‎ A．算法就是某个问题的解题过程；‎ B．算法执行后可以产生不同的结果；‎ C．解决某一个具体问题算法不同结果不同；‎ D．算法执行步骤的次数不可以很大，否则无法实施．‎ 解析：选项A ，算法不能等同于解法；选项B，例如：判断一个正整数是否为质数，结果为“是质数”和“不是质数”两种；选项C，解决某一个具体问题算法不同结果应该相同，否则算法构造的有问题；选项D，算法可以为很多次，但不可以无限次．选B．‎ ‎2、如图所示的程序框图中，则第3个输出的数是( ) ‎ A．1 B. C.2 D. ‎ ‎2.解析：前3个分别输出的数是1，，2.故选C.‎ 开始 结束 是 否 输出 ‎3．如图给出的是求的值的一个程序框图，‎ 其中判断框内应填入的条件是 （ ）‎ A.i>10? B.i<10? C.i>20? D.i<20?‎ 开始 结束 是 否 输出 ‎3．解析：通过列表,我们能清楚了解程序的每一步中的各个变量 是怎样变化的, 第一次:,‎ 第二次:,…依此可知循环的条件是i>10？．选Ａ ‎4.(2007年高考山东卷)阅读右边的程序框图，若输入的是100，则输出的变量和的值依次是（ ）‎ A．2550，2500 ‎ B．2550，2550 ‎ C．2500，2500 ‎ D．2500，2550‎ 开始 结束 是 否 输出 输入 ‎4.解析：依据框图可得 ‎，.选A. ‎ ‎5．2006年1月份开始实施的《个人所得税法》规定：全月总收入不超过元的免征个人工资、薪金所得税，超过元部分需征税．设全月总收入金额为元，前三级税率如下左表所示：‎ 级数 全月应纳税金额 税率 ‎1‎ 不超过元部分 ‎5%‎ ‎2‎ 超过至元部分 ‎10%‎ ‎3‎ 超过至元部分 ‎15%‎ ‎……‎ ‎……‎ ‎……‎ 开始 结束 输入x 输出0‎ 输出①‎ 输出②‎ ‎0n?‎ 输出S 结束 是 否 图2‎ ‎12、解：（Ⅰ）输出结果一致. 当n＝20时，‎ 图1的结果为2＋4＋6＋…＋38＋40＝2×（1＋2＋3＋…＋20）＝420 ‎ 图2的结果为2＋4＋6＋…＋38＋40＝2×（1＋2＋3＋…＋20）＝420 ‎ ‎（Ⅱ）修改后虚框部分的流程图为 ‎ ‎ ‎ S＝S+a a＝3﹡a i＝i+1‎ 第二节 算法的基本语句及算法案例 ‎※知识回顾 ‎1．任何一种程序设计语言都包含五种基本的算法语句，‎ 它们是输入语句 ， 输出语句， 赋值语句，条件语句，循环语句 ‎2.输入语句的一般格式是;‎ ‎   输出语句的一般格式是； ‎ ‎ 赋值语句的一般格式是； ‎ ‎   条件语句的一般格式是或； ‎ ‎ 循环语句的一般格式是和, .‎ 输入语句、 输出语句、 赋值语句基本对应于程序框图中的顺序结构；条件语句、循环语句分别用来表达程序框图中的条件结构和循环结构.‎ ‎3.常用符号 运算符号：加_+_，减-__，乘*__，除/__，乘方a^b，整数取商，求余数MOD.‎ 逻辑符号：且AND，或OR，大于>，等于=，小于<，大于等于>=，小于等于<=，不等于<>.‎ 常用函数：绝对值ABS，平方根SQR，取整INT.‎ ‎4.算法案例 ‎（1）辗转相除法和更相减损术 辗转相除法和更相减损术都是求两个正整数的最大公约数的方法.‎ ‎（1）辗转相除法就是对于给定的两个正整数，用大数除以小数，若余数不为0，则将小数和余数构成新的一对数，继续上面的除法，反复执行此步骤，直到大数被小数除尽，则这时较小的数就是原来两个数的最大公约数.‎ ‎（2）更相减损术就是对于给定的两个正整数，若它们都是偶数，则将它们反复除以2(假设进行了k次)，直到它们至少有一个不是偶数后，将大数减小数，然后将差和较小的数构成一对新数，继续上面的减法，反复执行此步骤，直到差和较小的数相等，此时相等的数再乘以原来约简的即为所求两数的最大公约数.‎ ‎（2）秦九韶算法 秦九韶算法是求多项式值的优秀算法.‎ 设，‎ 改写为如下形式：‎ 设 这样求n次多项式的值就转化为求n个一次多项式的值.当多项式中有些项不存在时，可将这几项看做，补齐后再利用秦九韶算法进行计算.对于一个n次多项式，只需做n次乘法和n次加法运算即可.‎ ‎（3）进位制 K进制数的基数为k，k进制数是由之间的数字构成的.‎ 将十进制的数转化为k进制数的方法是除k取余法.‎ ‎.‎ ‎※典例精析 例1．写出用循环语句描述求的值的算法程序.‎ 解：算法程序如下：‎ ‎（1）当型循环                        （2）直到型循环 ‎ ‎ 评注: 在编写算法的程序时，可先画出程序框图，抓住程序框图表示算法这个核心.注意分别用当型循环和直到型循环语句编写的程序中，循环条件的区别与联系. ‎ 例2、某市对排污水进行综合治理，征收污水处理费，系统对各厂一个月内排出的污水量吨收取的污水处理费元，运行程序如下所示：‎ 请写出y与m的函数关系，并求排放污水150吨的污水处理费用.‎ 解： 这个程序反映的是一个分段函数 因为所以，故该厂应缴纳污水处理费1400元.‎ 评注: 解决分段函数要用条件语句来处理.本题可画出程序框图帮助理解.‎ 例3． 求三个数72,120,168的最大公约数.‎ 解法1:用辗转相除法 先求120,168的最大公约数,‎ 因为       ‎ 所以120,168的最大公约数是24.‎ 再求72,24的最大公约数,‎ 因为,所以72,24的最大公约数为24,‎ 即72,120,168的最大公约数为24.‎ 解法2:用更相减损术 先求120,168的最大公约数,‎ ‎168-120=48,120-48=72,72-48=24,48-24=24‎ 所以120,168的最大公约数为24.‎ 再求72,24的最大公约数,‎ ‎72-24=48，48-24=24‎ ‎72,24的最大公约数为24,‎ 即72,120,168的最大公约数为24.‎ 评注: 辗转相除法与更相减损术均是求两个正整数的最大公约数的方法,要理解和掌握它们的操作步骤.‎ 变式:试写出求正整数的最小公倍数的算法程序.‎ 解:‎ 或 例4.用秦九韶算法求多项式在时的值.‎ 分析：先改写多项式，再由内向外计算.‎ 评注: 用秦九韶算法求多项式值,关健是正确将多项式改写,然后由内向外计算求得.‎ 本题也可简写为下式：‎ 例5.完成下列进制的转化 ‎ ‎ 解: ‎ ‎(2)用8反复去除101,直到商为0止,所得的余数(从末位读起)就是十进制数101的 ‎8进制表示 ‎   所以 评注:将进制的数转化为进制的数的方法是先将进制的数转化为十进制的数，再将这个数转化为进制的数.‎ 变式训练：下面是把二进制数化为十进制数的一个程序框图,判断框内应填入的条件是 ‎     ( )‎ 解: ,故判断框内应填入的条件.选C.‎ ※ 基础自测 一、选择题 ‎1．下列给出的赋值语句中正确的是（ ）‎ A B C D ‎ ‎1. 解析:赋值语句的功能.选 B ‎ ‎2 当时，下面的程序输出的结果是 ( )‎ A B C D ‎ ‎2解析： . 选 C ‎ ‎3．运行下列程序：‎ ‎　当输入56，42时，输出的结果是 ‎　Ａ．56　　　　 Ｂ．42　‎ ‎ Ｃ．84　　 Ｄ．14‎ ‎3.解析:该程序的功能是用辗转相除法求正整数的最大公约数，故选D ‎4下边程序运行后输出的结果为( )‎ ‎ ‎ A B C D ‎ ‎4.解析:.选 D ‎ 二、填空题 ‎5 三个数的最大公约数是_________________ ‎ ‎5 解析:.填 ‎6.‎ 阅读下列程序:‎ ‎     ‎ 当程序输入值为123时,问运行的结果是_____________.‎ ‎6.解析:算术运算符和MOD分别用取商和余数.该程序的功能是把一个三位数各位上的数字颠倒过来.所以运行的结果是321.‎ ‎7．（2005年高考北京卷理14）已知n次多项式，如果在一种算法中，计算（k＝2，3，4，…，n）的值需要k－1次乘法，计算的值共需要9次运算（6次乘法，3次加法），那么计算的值共需要 次运算.下面给出一种减少运算次数的算法：（k＝0， 1，2，…，n－1）．利用该算法，计算的值共需要6次运算，计算的值共需要 次运算.‎ ‎7．解析：秦九韶算法适用一般的多项式的求值问题.直接法乘法运算的次数最多可到达，加法最多n次.秦九韶算法通过转化把乘法运算的次数减少到最多n次，加法最多n次.答案：65；20.‎ ‎8．下面程序运行后输出的结果为_______________ ‎ ‎8．解析: 22，-22‎ 三、解答题 ‎9.用秦九韶算法求多项式在时的值.‎ ‎10．设计程序，求出满足的最小的正整数n.‎ ‎10．解：‎ ‎11‎ 若,试判断的大小关系，并将化为7进制的数.‎ ‎6.解析: ‎ ‎12.某电信公司规定：拨打市内电话时，如果不超过3分钟，则收取话费0.2元；如果通话时间超过3分钟，则超出部分按每分钟0.1元收取通话费，不足一分钟按一分钟计算.设通话时间为t（分钟），通话费用y（元），如何设计一个程序，计算通话的费用.‎ ‎(提示:INT(x)表示不大于x最大整数,如INT(3.2)=3)‎ ‎12．解：算法分析：‎ 数学模型实际上为：y关于t的分段函数.关系是如下：‎ 其中[t－3]表示取不大于t－3的整数部分.‎ 算法步骤如下：‎ 第一步：输入通话时间t；‎ 第二步：如果t≤3，那么y = 0.2；否则判断t∈Z 是否成立，‎ 若成立执行y= 0.2+0.1× (t－3)；否则执行y = 0.2+0.1×（ [t－3]+1）.‎ 第三步：输出通话费用c .‎ 算法程序如下：‎ ‎ ‎