2019-2020学年新教材高中物理第1章功和机械能章末复习课教案鲁科版必修第二册 6页

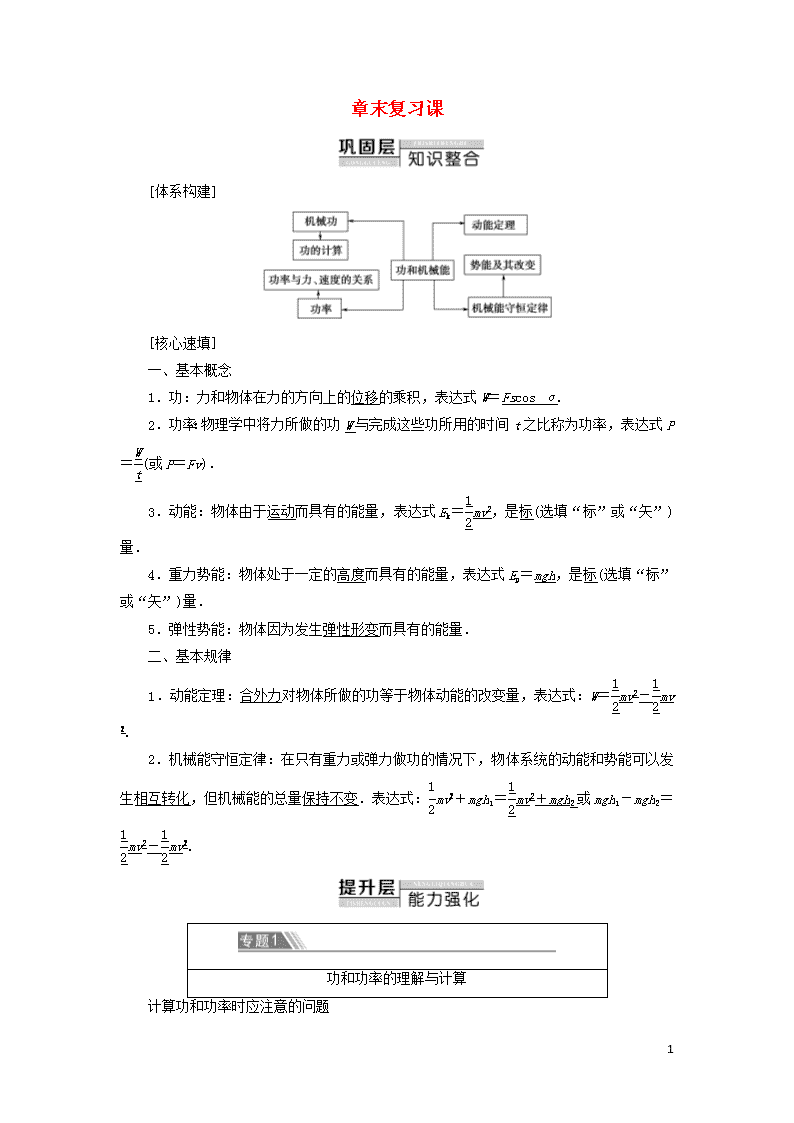
章末复习课 ‎[体系构建]‎ ‎[核心速填]‎ 一、基本概念 ‎1．功：力和物体在力的方向上的位移的乘积，表达式W＝Fscos α.‎ ‎2．功率：物理学中将力所做的功W与完成这些功所用的时间t之比称为功率，表达式P＝(或P＝Fv)．‎ ‎3．动能：物体由于运动而具有的能量，表达式Ek＝mv2，是标(选填“标”或“矢”)量．‎ ‎4．重力势能：物体处于一定的高度而具有的能量，表达式Ep＝mgh，是标(选填“标”或“矢”)量．‎ ‎5．弹性势能：物体因为发生弹性形变而具有的能量．‎ 二、基本规律 ‎1．动能定理：合外力对物体所做的功等于物体动能的改变量，表达式：W＝mv－mv.‎ ‎2．机械能守恒定律：在只有重力或弹力做功的情况下，物体系统的动能和势能可以发生相互转化，但机械能的总量保持不变．表达式：mv＋mgh1＝mv＋mgh2或mgh1－mgh2＝mv－mv.‎ 功和功率的理解与计算 计算功和功率时应注意的问题 6‎ ‎(1)计算功时，要注意分析受力情况和能量转化情况，分清是恒力做功，还是变力做功，恒力做功一般用功的公式或动能定理求解，变力做功用动能定理或图像法求解．‎ ‎(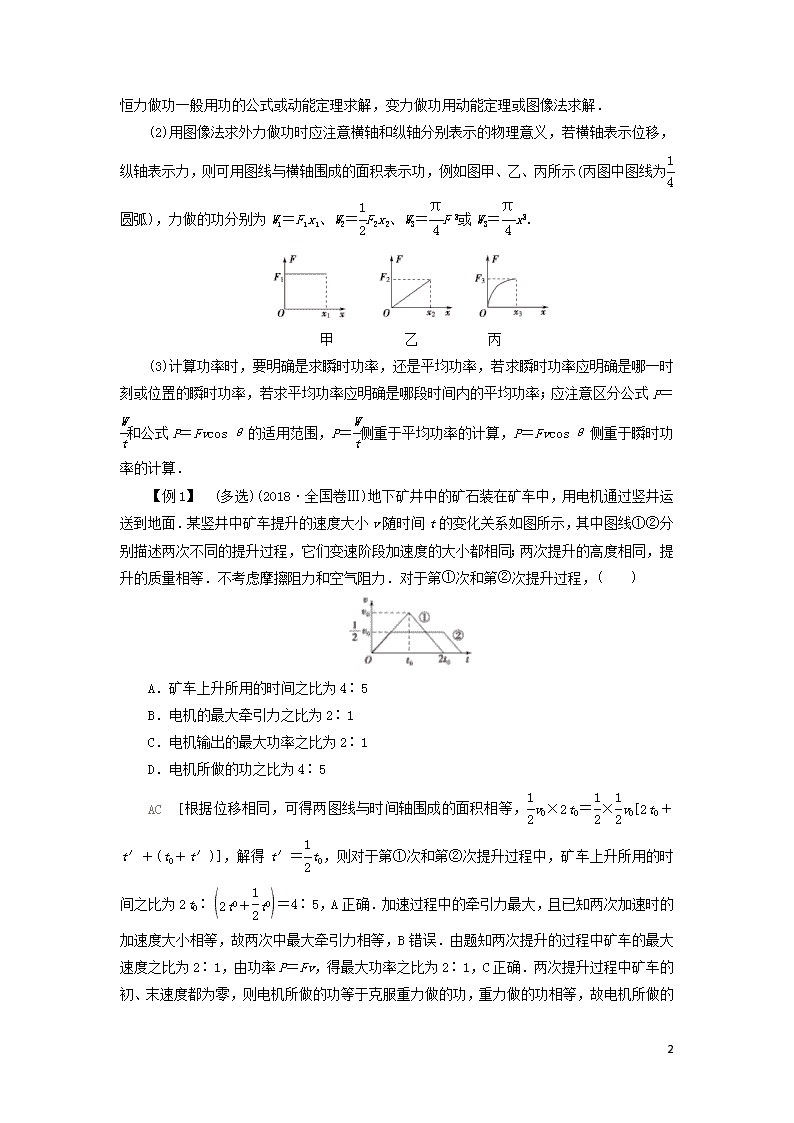2)用图像法求外力做功时应注意横轴和纵轴分别表示的物理意义，若横轴表示位移，纵轴表示力，则可用图线与横轴围成的面积表示功，例如图甲、乙、丙所示(丙图中图线为圆弧)，力做的功分别为W1＝F1x1、W2＝F2x2、W3＝F或W3＝x.‎ 甲　　　　　乙　　　　　丙 ‎(3)计算功率时，要明确是求瞬时功率，还是平均功率，若求瞬时功率应明确是哪一时刻或位置的瞬时功率，若求平均功率应明确是哪段时间内的平均功率；应注意区分公式P＝和公式P＝Fvcos θ的适用范围，P＝侧重于平均功率的计算，P＝Fvcos θ侧重于瞬时功率的计算．‎ ‎【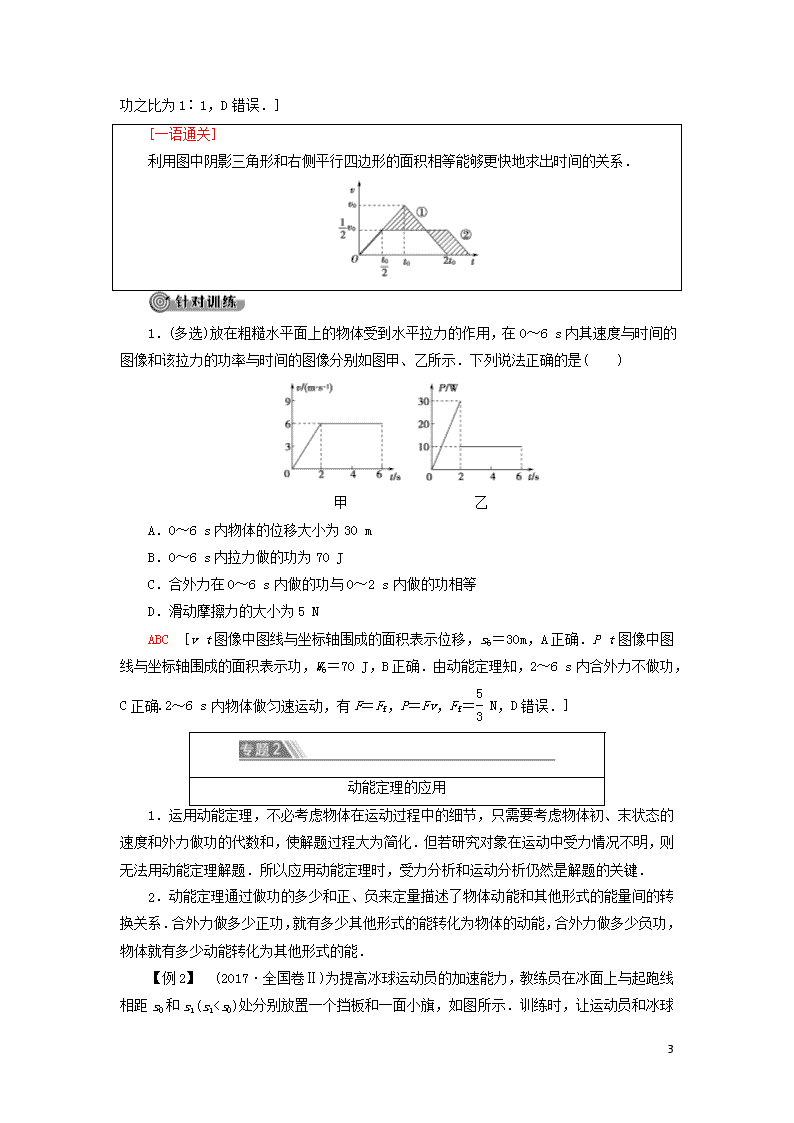例1】　(多选)(2018·全国卷Ⅲ)地下矿井中的矿石装在矿车中，用电机通过竖井运送到地面．某竖井中矿车提升的速度大小v随时间t的变化关系如图所示，其中图线①②分别描述两次不同的提升过程，它们变速阶段加速度的大小都相同；两次提升的高度相同，提升的质量相等．不考虑摩擦阻力和空气阻力．对于第①次和第②次提升过程，(　　)‎ A．矿车上升所用的时间之比为4∶5‎ B．电机的最大牵引力之比为2∶1‎ C．电机输出的最大功率之比为2∶1‎ D．电机所做的功之比为4∶5‎ AC　[根据位移相同，可得两图线与时间轴围成的面积相等，v0×2t0＝×v0[2t0＋t′＋(t0＋t′)]，解得t′＝t0，则对于第①次和第②次提升过程中，矿车上升所用的时间之比为2t0∶＝4∶5，A正确．加速过程中的牵引力最大，且已知两次加速时的加速度大小相等，故两次中最大牵引力相等，B错误．由题知两次提升的过程中矿车的最大速度之比为2∶1，由功率P＝Fv，得最大功率之比为2∶1，C正确．两次提升过程中矿车的初、末速度都为零，则电机所做的功等于克服重力做的功，重力做的功相等，故电机所做的功之比为1∶1，D错误．]‎ 6‎ ‎[一语通关]　‎ 利用图中阴影三角形和右侧平行四边形的面积相等能够更快地求出时间的关系．‎ ‎1．(多选)放在粗糙水平面上的物体受到水平拉力的作用，在0～6 s内其速度与时间的图像和该拉力的功率与时间的图像分别如图甲、乙所示．下列说法正确的是(　　)‎ 甲　　　　　　　　　乙 A．0～6 s内物体的位移大小为30 m B．0～6 s内拉力做的功为70 J C．合外力在0～6 s内做的功与0～2 s内做的功相等 D．滑动摩擦力的大小为5 N ABC　[vt图像中图线与坐标轴围成的面积表示位移，s6＝30 m，A正确．Pt图像中图线与坐标轴围成的面积表示功，W6＝70 J，B正确．由动能定理知，2～6 s内合外力不做功，C正确.2～6 s内物体做匀速运动，有F＝Ff，P＝Fv，Ff＝ N，D错误．]‎ 动能定理的应用 ‎1．运用动能定理，不必考虑物体在运动过程中的细节，只需要考虑物体初、末状态的速度和外力做功的代数和，使解题过程大为简化．但若研究对象在运动中受力情况不明，则无法用动能定理解题．所以应用动能定理时，受力分析和运动分析仍然是解题的关键．‎ ‎2．动能定理通过做功的多少和正、负来定量描述了物体动能和其他形式的能量间的转换关系．合外力做多少正功，就有多少其他形式的能转化为物体的动能，合外力做多少负功，物体就有多少动能转化为其他形式的能．‎ ‎【例2】　(2017·全国卷Ⅱ)为提高冰球运动员的加速能力，教练员在冰面上与起跑线相距s0和s1(s1