【新教材】2020-2021学年高中人教A版数学必修第二册习题：8-6-1　直线与直线垂直 5页

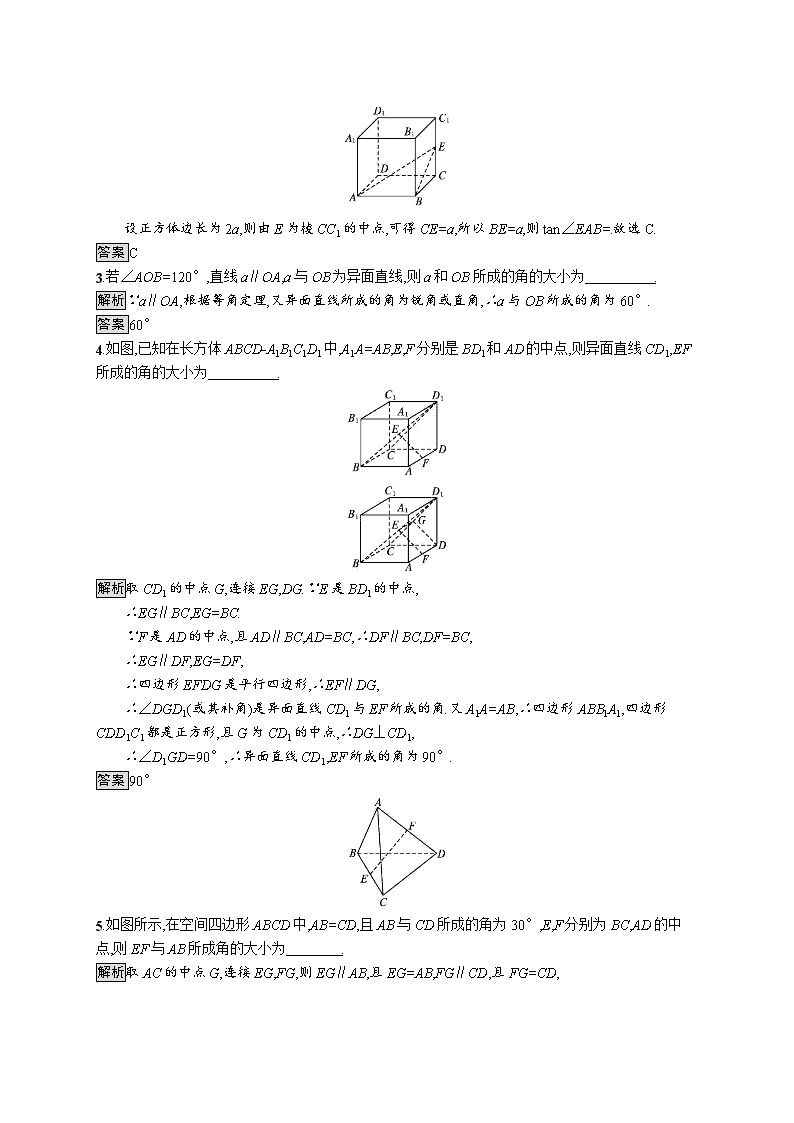
‎8.6　空间直线、平面的垂直 ‎8.6.1　直线与直线垂直 课后篇巩固提升 基础达标练 ‎　　 　　　　　　　　　　　　　　‎ ‎1.‎ 如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则EF和AC所成的角等于(　　)‎ A.30° B.45°‎ C.60° D.90°‎ 解析如图所示,取BC的中点G,连接FG,EG.‎ ‎∵E,F分别为CD,AB的中点,∴FG∥AC,EG∥BD,‎ 且FG=AC,EG=BD.‎ ‎∵AC=BD,∴FG=EG,‎ ‎∴∠EFG(或其补角)为EF与AC所成的角.‎ ‎∵AC⊥BD,∴FG⊥EG,∴∠FGE=90°,‎ ‎∴△EFG为等腰直角三角形.‎ ‎∴∠EFG=45°,即EF与AC所成的角为45°.‎ 答案B ‎2.(2020海南华侨中学高三月考)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为(　　)‎ A. B. C. D.‎ 解析在正方体ABCD-A1B1C1D1中,CD∥AB,‎ 所以异面直线AE与CD所成角为∠EAB,‎ 设正方体边长为2a,则由E为棱CC1的中点,可得CE=a,所以BE=a,则tan∠EAB=.故选C.‎ 答案C ‎3.若∠AOB=120°,直线a∥OA,a与OB为异面直线,则a和OB所成的角的大小为　　　　　. ‎ 解析∵a∥OA,根据等角定理,又异面直线所成的角为锐角或直角,∴a与OB所成的角为60°.‎ 答案60°‎ ‎4.如图,已知在长方体ABCD-A1B1C1D1中,A1A=AB,E,F分别是BD1和AD的中点,则异面直线CD1,EF所成的角的大小为　　　　　. 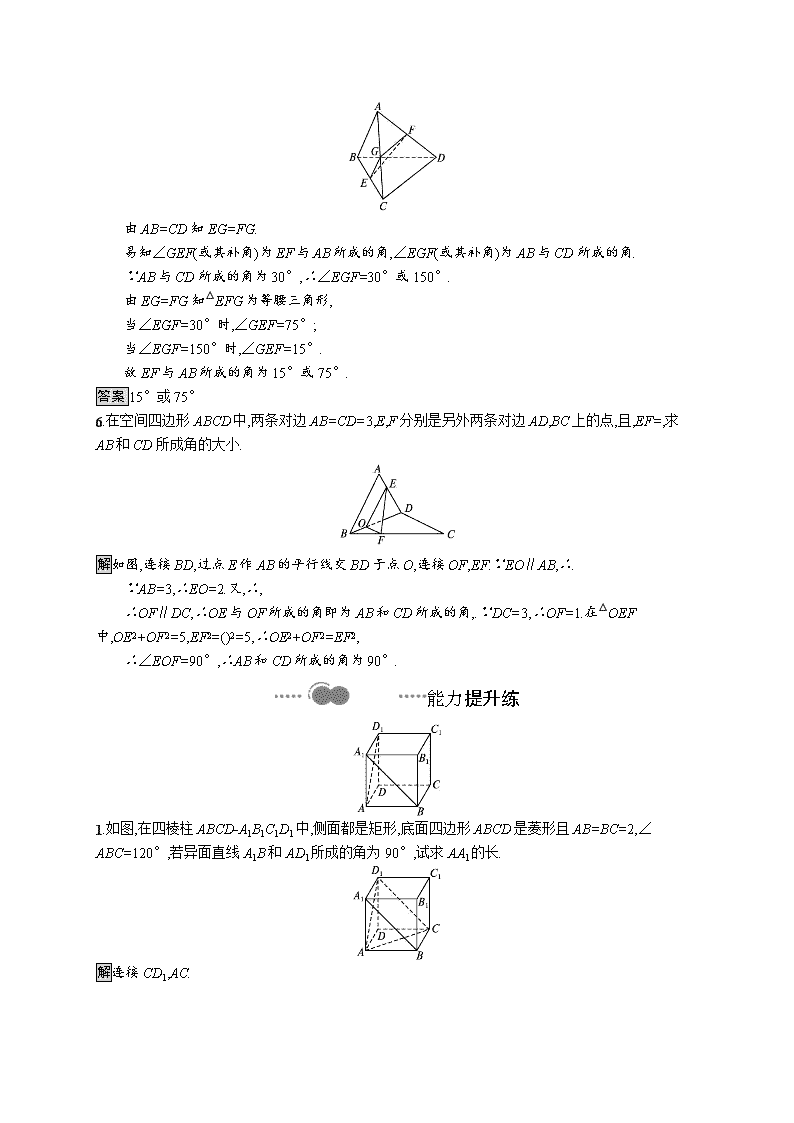‎ 解析取CD1的中点G,连接EG,DG.∵E是BD1的中点,‎ ‎∴EG∥BC,EG=BC.‎ ‎∵F是AD的中点,且AD∥BC,AD=BC,∴DF∥BC,DF=BC,‎ ‎∴EG∥DF,EG=DF,‎ ‎∴四边形EFDG是平行四边形,∴EF∥DG,‎ ‎∴∠DGD1(或其补角)是异面直线CD1与EF所成的角.又A1A=AB,∴四边形ABB1A1,四边形CDD1C1都是正方形,且G为CD1的中点,∴DG⊥CD1,‎ ‎∴∠D1GD=90°,∴异面直线CD1,EF所成的角为90°.‎ 答案90°‎ ‎5.如图所示,在空间四边形ABCD中,AB=CD,且AB与CD所成的角为30°,E,F分别为BC,AD的中点,则EF与AB所成角的大小为　　　　. ‎ 解析取AC的中点G,连接EG,FG,则EG∥AB,且EG=AB,FG∥CD,且FG=CD,‎ 由AB=CD知EG=FG.‎ 易知∠GEF(或其补角)为EF与AB所成的角,∠EGF(或其补角)为AB与CD所成的角.‎ ‎∵AB与CD所成的角为30°,∴∠EGF=30°或150°.‎ 由EG=FG知△EFG为等腰三角形,‎ 当∠EGF=30°时,∠GEF=75°;‎ 当∠EGF=150°时,∠GEF=15°.‎ 故EF与AB所成的角为15°或75°.‎ 答案15°或75°‎ ‎6.在空间四边形ABCD中,两条对边AB=CD=3,E,F分别是另外两条对边AD,BC上的点,且,EF=,求AB和CD所成角的大小.‎ 解如图,连接BD,过点E作AB的平行线交BD于点O,连接OF,EF.∵EO∥AB,∴.‎ ‎∵AB=3,∴EO=2.又,∴,‎ ‎∴OF∥DC,∴OE与OF所成的角即为AB和CD所成的角,.∵DC=3,∴OF=1.在△OEF中,OE2+OF2=5,EF2=()2=5,∴OE2+OF2=EF2,‎ ‎∴∠EOF=90°,∴AB和CD所成的角为90°.‎ 能力提升练 ‎1.如图,在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面四边形ABCD是菱形且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,试求AA1的长.‎ 解连接CD1,AC.‎ 由题意得在四棱柱ABCD-A1B1C1D1中,A1D1∥BC,A1D1=BC,∴四边形A1BCD1是平行四边形,∴A1B∥CD1,∴∠AD1C(或其补角)为A1B和AD1所成的角.∵异面直线A1B和AD1所成的角为90°,∴∠AD1C=90°.‎ ‎∵四棱柱ABCD-A1B1C1D1中,AB=BC=2,‎ ‎∴△ACD1是等腰直角三角形,‎ ‎∴AD1=AC.∵底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,‎ ‎∴AC=2×sin 60°×2=6,AD1=AC=3,‎ ‎∴AA1=.‎ ‎2.‎ 如图,空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于点E,F,G,H.E在AB的何处时截面EFGH的面积最大?最大面积是多少?‎ 解∵AD与BC成60°角,‎ ‎∴∠HGF=60°或120°.‎ 设AE∶AB=x,则=x.又BC=a,‎ ‎∴EF=ax.‎ 由=1-x,得EH=a(1-x).‎ ‎∴S四边形EFGH=EF×EH×sin 60°=ax×a(1-x)×a2(-x2+x)=a2.‎ 当x=时,S最大值=a2,即当E为AB的中点时,截面的面积最大,最大面积为a2.‎ 素养培优练 ‎　如图,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB的中点,则EF的长是(　　)‎ A.1 B. C. D.‎ 解析取CB的中点D,连接ED,DF,则∠EDF(或其补角)为异面直线SB与AC所成的角,即∠EDF=90°.‎ 在△EDF中,ED=SB=1,DF=AC=1,所以EF=.‎ 答案B