2019届高考数学（理）二轮复习专题透析课件和讲义专题2　三角函数与解三角形 10页

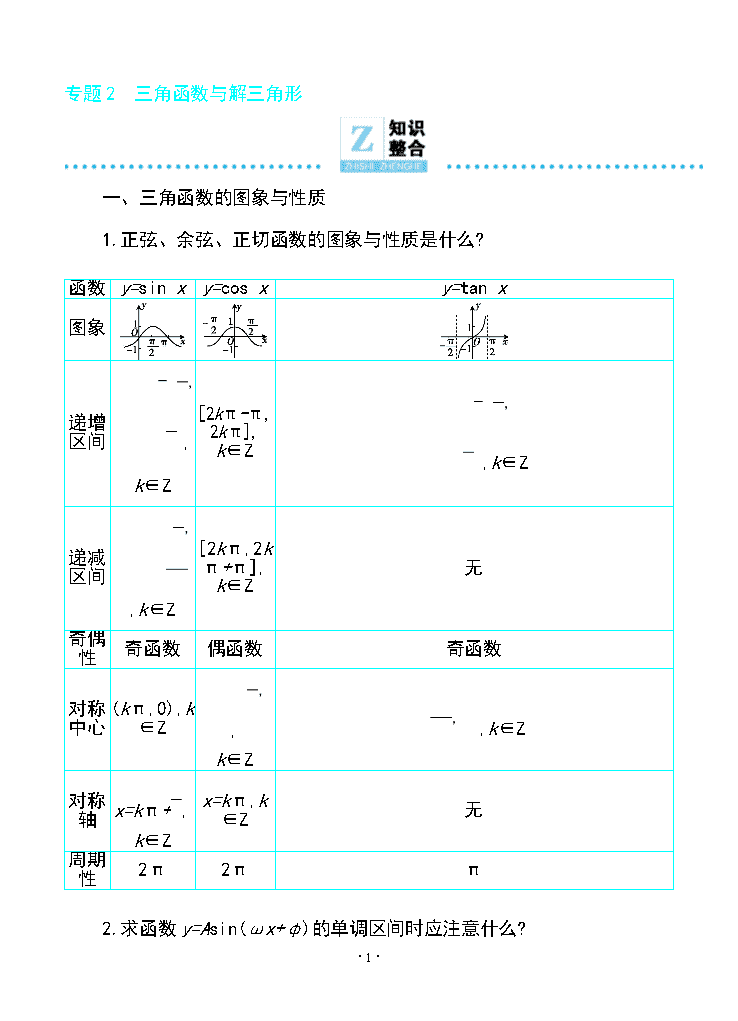
专题2　三角函数与解三角形 ‎　　一、三角函数的图象与性质 ‎　　1.正弦、余弦、正切函数的图象与性质是什么?‎ 函数 y=sin x y=cos x y=tan x 图象 递增 区间 ‎,k∈Z ‎[2kπ-π,2kπ],‎ k∈Z ‎,k∈Z 递减 区间 ‎,k∈Z ‎[2kπ,2kπ+π],‎ k∈Z 无 奇偶性 奇函数 偶函数 奇函数 对称 中心 ‎(kπ,0),k∈Z ‎,‎ k∈Z ‎,k∈Z 对称轴 x=kπ+,‎ k∈Z x=kπ,k∈Z 无 周期性 ‎2π ‎2π π ‎　　2.求函数y=Asin(ωx+φ)的单调区间时应注意什么?‎ ‎·10·‎ ‎(1)注意ω的符号,不要把单调性或区间左右的值弄反;‎ ‎(2)不要忘记写“+2kπ”或“+kπ”等,特别注意不要忘掉写“k∈Z”;‎ ‎(3)书写单调区间时,不要把弧度和角度混在一起.‎ ‎3.三角函数的常用结论有哪些?‎ ‎(1)对于y=Asin(ωx+φ),当φ=kπ(k∈Z)时,其为奇函数;当φ=kπ+(k∈Z)时,其为偶函数;对称轴方程可由ωx+φ=kπ+(k∈Z)求得.‎ ‎(2)对于y=Acos(ωx+φ),当φ=kπ+(k∈Z)时,其为奇函数;当φ=kπ(k∈Z)时,其为偶函数;对称轴方程可由ωx+φ=kπ(k∈Z)求得.‎ ‎(3)对于y=Atan(ωx+φ),当φ=kπ(k∈Z)时,其为奇函数.‎ ‎4.三角函数图象的两种常见变换是什么?‎ ‎(1)y=sin xy=sin(x+φ)y=sin(ωx+φ)y=Asin(ωx+φ).(A>0,ω>0)‎ ‎(2)y=sin xy=sin ωxy=sin(ωx+φ)‎ y=Asin(ωx+φ).(A>0,ω>0)‎ ‎　　二、三角恒等变换与解三角形 ‎　　1.同角关系公式有哪些?如何记忆诱导公式?‎ ‎(1)同角关系:sin2α+cos2α=1,=tan α.‎ ‎·10·‎ ‎(2)诱导公式,对于“±α,k∈Z的三角函数值”与“角α的三角函数值”的关系可按下面口诀记忆:奇变偶不变,符号看象限.‎ ‎2.你能写出两角和与差的正弦、余弦、正切公式及倍角、辅助角公式吗?‎ ‎(1)两角和与差的正弦、余弦、正切公式:‎ sin(α±β)=sin αcos β±cos αsin β;‎ cos(α±β)=cos αcos β∓sin αsin β;‎ tan(α±β)=.‎ ‎(2)二倍角公式:sin 2α=2sin αcos α,‎ cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.‎ ‎(3)辅助角公式:asin x+bcos x=sin(x+φ),其中tan φ=.‎ ‎3.在三角恒等变换中,常见的拆角、拼角技巧有哪些?‎ α=(α+β)-β,2α=(α+β)+(α-β),α=[(α+β)+(α-β)],α+=(α+β)-,α=-.‎ ‎　　4.正弦定理、余弦定理、三角形面积公式是什么?‎ 在△ABC中,角A,B,C的对边分别为a,b,c.‎ ‎(1)正弦定理:‎ 在△ABC中,===2R(R为△ABC的外接圆半径).‎ ‎·10·‎ 变形:a=2Rsin A,sin A=,a∶b∶c=sin A∶sin B∶sin C.‎ ‎(2)余弦定理:‎ 在△ABC中,a2=b2+c2-2bccos A.‎ 变形:b2+c2-a2=2bccos A,cos A=.‎ ‎(3)三角形面积公式:‎ S△ABC=absin C=bcsin A=acsin B.‎ ‎5.已知三角形两边及其一边的对角,用正弦定理解三角形时要注意什么?‎ 若运用正弦定理,则务必注意可能有两解,要结合具体情况进行取舍.在△ABC中,A>B⇔sin A>sin B.‎ 三角函数与解三角形是高考考查的重点和热点.三角函数的定义、图象、性质以及简单的化简与求值主要以选择题、填空题的形式考查.其中同角三角函数的基本关系、诱导公式、两角和差公式、二倍角公式是解决化简、计算问题的工具,“角”的变换是三角恒等变换的核心.解三角形多以解答题的形式考查,常与三角恒等变换结合,主要考查边、角、面积的计算及有关的范围问题.‎ ‎　　一、选择题和填空题的命题特点 ‎·10·‎ ‎(一)三角函数的图象与性质是高考考查的重点和热点,考查主要从以下两个方面进行:(1)三角函数的图象,主要涉及图象变换以及由图象确定解析式;(2)利用三角函数的性质求解三角函数中有关值、参数、最值、值域、单调区间等问题.‎ ‎　　　　　　　　　　　　　　　　　‎ ‎1.(2018·全国Ⅰ卷·文T8改编)已知函数f(x)=2cos22x+5,则(　　).‎ A.f(x)的最小正周期为π,最大值为7‎ B.f(x)的最小正周期为2π,最小值为5‎ C.f(x)的最小正周期为2π,最大值为7‎ D.f(x)的最小正周期为,最小值为5‎ ‎　　解析▶　f(x)=cos222x+5=cos 4x+6,故f(x)的最小正周期为,最大值为7,最小值为5.‎ ‎　　答案▶　D ‎2.(2016·全国Ⅱ卷·理T7改编)若将函数f(x)=sin 2x的图象向右平移个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一个对称中心是(　　).‎ A. B.‎ C. D.‎ ‎　　解析▶　由题意可知函数f(x)=sin 2x的图象向右平移 ‎·10·‎ 个单位长度,得到函数g(x)=sin=sin的图象.‎ 令2x-=kπ(k∈Z),得x=+(k∈Z),‎ 由此可得y=g(x)图象的一个对称中心是,故选D.‎ ‎　　答案▶　D ‎(二)三角函数的化简与求值是高考的命题热点,其中同角三角函数的基本关系、诱导公式是解决问题的工具,三角恒等变换是利用三角恒等式(两角和与差公式,二倍角的正弦、余弦、正切公式)进行变换.“角”的变换是三角恒等变换的核心.‎ ‎3.(2018·全国Ⅱ卷·理T15改编)已知sin α+cos β=,sin β-cos α=1,则sin(α-β)=(　　).‎ A.- B.-‎ C. D.‎ ‎　　解析▶　将sin α+cos β=的等式两边平方得sin2αcos+2β+2sin αcos β=,　①‎ 将sin β-cos α=1的等式两边平方得sin2β+cos2α-2sin βcos α=1.　②‎ ‎·10·‎ ‎①+②得sin(α-β)=-,故选B.‎ ‎　　答案▶　B ‎4.(2018·全国Ⅲ卷·文T4改编)已知tan θ=,则sin 2θ-2cos2θ=(　　).‎ A.-1 B.- C. D.-‎ ‎　　解析▶　sin 2θ-cos22θ====-,故选B.‎ ‎　　答案▶　B ‎(三)正弦定理与余弦定理以及解三角形问题是高考的必考内容,主要考查边、角、面积的计算及有关的范围问题.‎ ‎5.(2018·全国Ⅰ卷·文T16改编)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若bsin C+csin B=4asin Bsin C,且2bsin B+2csin C=bc+a,则△ABC面积的最大值为(　　).‎ A. B. C. D.‎ ‎　　解析▶　根据题意,结合正弦定理可得 sin Bsin C+sin Csin B=4sin Asin Bsin C,‎ 即sin A=.‎ ‎·10·‎ ‎∵2bsin B+2csin C=bc+a,‎ ‎∴bsin B+csin C=bc+a,‎ ‎∴bsin B+csin C=bcsin A+asin A,‎ 则b2+c2=abc+a2.‎ 由余弦定理可得2bccos A=abc,解得a=2cos A=.‎ 由b2+c2=bc+3≥2bc,得bc≤3,从而S△ABC=bcsin A≤,故选C.‎ ‎　　答案▶　C ‎6.(2018·全国Ⅲ卷·文T11改编)在△ABC中,内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tan C=(　　).‎ A.- B.- C. D.‎ ‎　　解析▶　∵2S=(a+b)2-c2,‎ ‎∴absin C=(a+b)2-c2=a2+b2-c2+2ab=2abcos C+2ab,‎ ‎∴sin C=2cos C+2,‎ ‎∴sin2C=(2cos C+2)2=1-cos2C,‎ 即5cos2C+8cos C+3=0,‎ ‎∴cos C=-(cos C=-1舍去),‎ ‎∴sin C=,tan C==-,故选B.‎ ‎·10·‎ ‎　　答案▶　B ‎　　二、解答题的命题特点 高考全国卷中有关解三角形的解答题,主要涉及利用正、余弦定理求三角形的边长、角、面积等基本计算,两个定理与三角恒等变换的结合.这类试题一般要用到三角形的内角和定理,正、余弦定理及有关三角形的性质.‎ ‎(2018·全国Ⅰ卷·理T17改编)如图,在四边形ABCD中,cos∠DAB=-,=,BD=4,AB⊥BC.‎ ‎(1)求sin∠ABD的值;‎ ‎(2)若∠BCD=,求CD的长.‎ ‎　　解析▶　(1)因为=,所以设AD=2k,AB=3k,其中k>0.‎ 在△ABD中,由余弦定理得BD2=AB2+AD2-2AB·AD·cos∠DAB,所以16=9k2+4k2-2×3k×2k×,解得k=1,则AD=2,‎ 而sin∠DAB==.‎ 在△ABD中,由正弦定理得sin∠ABD=sin∠DAB=×=.‎ ‎·10·‎ ‎(2)由(1)可知,sin∠ABD=,而AB⊥BC,‎ 则sin∠CBD=sin=cos∠ABD==.‎ 在△BCD中,∠BCD=,‎ 由正弦定理得 CD=·BD=×4=.‎ 关于解三角形问题,一般要用到三角形的内角和定理,正、余弦定理及有关三角形的性质,常见的三角恒等变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”.‎ ‎·10·‎