- 66.50 KB
- 2021-06-09 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时分层作业(五) 同角三角函数的基本关系
(建议用时:40分钟)
[学业达标练]
一、选择题
1.已知α是第三象限角,且sin α=-,则3cos α+4tan α=( )
【导学号:84352046】
A.- B.
C.- D.
A [因为α是第三象限角,且sin α=-,
所以cos α=-=-=-,
所以tan α===,
所以3cos α+4tan α=-2+=-.]
2.化简sin2α+cos4α+sin2αcos2α的结果是( )
A. B.
C.1 D.
C [原式=sin2α+cos2α(cos2α+sin2α)
=sin2α+cos2α=1.]
3.已知sin α=,则sin4α-cos4α的值为( )
A.- B.-
C. D.
B [sin4α-cos4α=(sin2α+cos2α)(sin2α-cos2α)=sin2α-cos2α=2sin2α-1=-.]
4.cos2x等于( )
【导学号:84352047】
A.tan x B.sin x
C.cos x D.
5
D [原式=·cos2x
=·cos2x
=·cos2x==.]
5.已知sin θ+cos θ=,则sin θ-cos θ=( )
A. B.-
C. D.-
B [由(sin θ+cos θ)2=1+2sin θcos θ=,得2sin θcos θ=,则(sin θ-cos θ)2=1-2sin θcos θ=,由0<θ≤,知sin θ-cos θ≤0,所以sin θ-cos θ=-.]
二、填空题
6.化简的结果是________.
cos 20° [==
==|cos 20°|=cos 20°.]
7.已知cos α+2sin α=-,则tan α=________.
2 [由得(sin α+2)2=0,
∴sin α=-,cos α=-,∴tan α=2.]
8.已知tan α=2,则4sin2α-3sin αcos α-5cos2α=________.
【导学号:84352048】
1 [4sin2α-3sin αcos α-5cos2α
=
=
===1.]
5
三、解答题
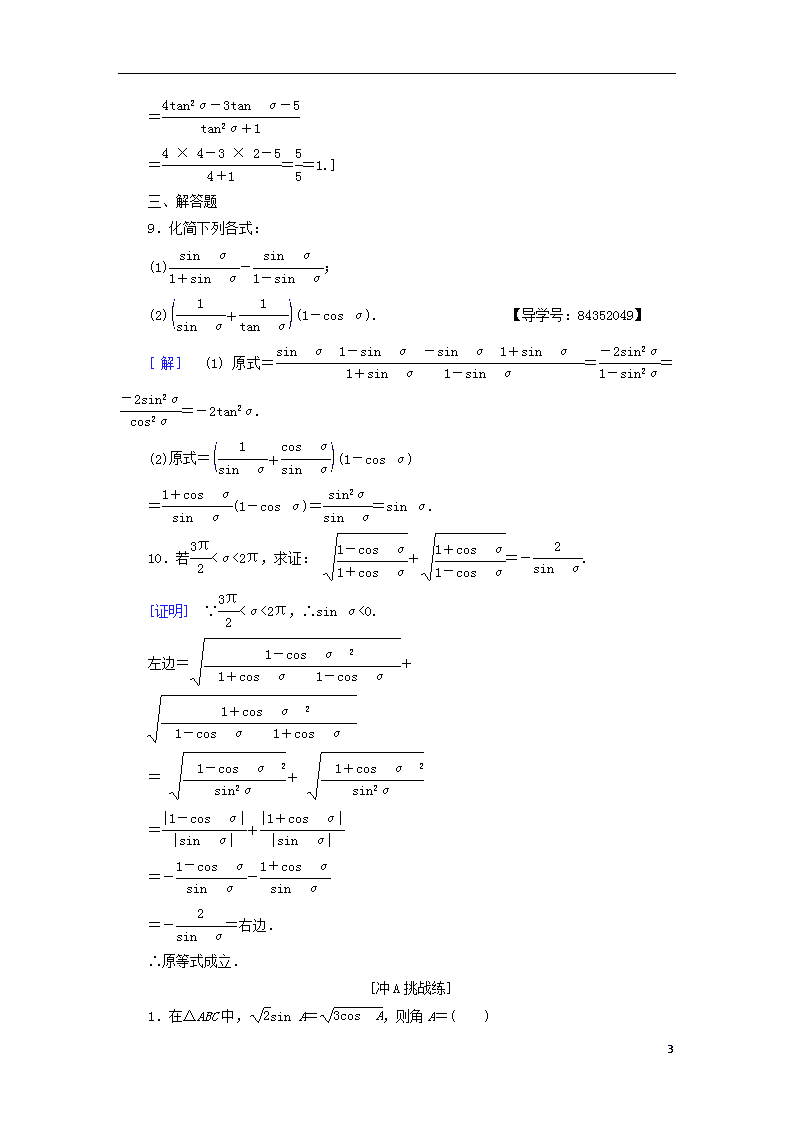
9.化简下列各式:
(1)-;
(2)(1-cos α). 【导学号:84352049】
[解] (1)原式====-2tan2α.
(2)原式=(1-cos α)
=(1-cos α)==sin α.
10.若<α<2π,求证: +=-.
[证明] ∵<α<2π,∴sin α<0.
左边=+
= +
=+
=--
=-=右边.
∴原等式成立.
[冲A挑战练]
1.在△ABC中,sin A=,则角A=( )
A. B.
C. D.
C [由题意知cos A>0,即A为锐角.
将sin A=两边平方得2sin2A=3cos A,
∴2cos2A+3cos A-2=0,
5
解得cos A=或cos A=-2(舍去).
∴A=.]
2.的值为( )
【导学号:84352050】
A.1 B.-1
C.sin 10° D.cos 10°
B [
==
==-1.]
3.已知sin θ=,cos θ=,则m的值为________.
0或8 [因为sin2θ+cos2θ=1,所以2+2=1.
整理得m2-8m=0,解得m=0或8.]
4.已知sin θ,cos θ是方程2x2-mx+1=0的两根,则+=________.
± [+=+=+==sin θ+cos θ,又因为sin θ,cos θ是方程2x2-mx+1=0的两根,所以由根与系数的关系得sin θcos θ=,则(sin θ+cos θ)2=1+2sin θcos θ=2,所以sin θ+cos θ=±.]
5.求证:=.
【导学号:84352051】
[证明] 法一:右边==
5
=
=
=
==左边.
所以原等式成立.
法二:左边=
=
=.
右边==
=.
所以原等式成立.
5
相关文档
- 2020高中数学 第二章 基本初等函数2021-06-094页
- 2020版高中数学 第三章 不等式 同2021-06-095页
- 高中数学选修2-3配套课件3_2独立性2021-06-0935页
- 2020_2021学年新教材高中数学第5章2021-06-098页
- 高中数学(人教版必修2)配套练习 第四2021-06-094页
- 高中数学必修2同步练习:直线与圆的2021-06-095页
- 高中数学必修2教案:第四章至第二部2021-06-0986页
- 高中数学必修2教案:柱、锥、台和球2021-06-091页
- 高中数学(人教A版)必修4:2-1同步试题(2021-06-096页
- 数学文卷·2017届江西省百所重点高2021-06-0910页