2020高中数学 第一章 解三角形 1.2.1 平面的基本性质与推论 4页

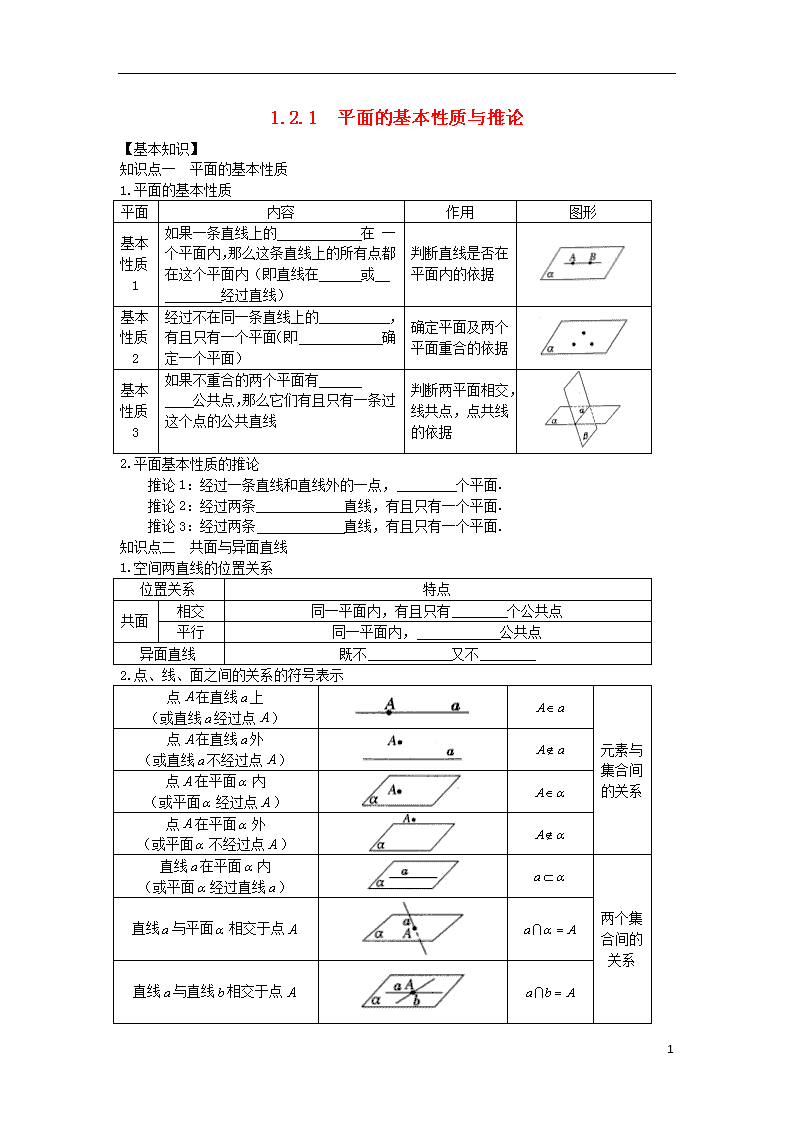
‎1.2.1　‎平面的基本性质与推论 ‎【基本知识】‎ 知识点一　平面的基本性质 ‎1.平面的基本性质 平面 内容 作用 图形 基本性质1‎ 如果一条直线上的 在一个平面内，那么这条直线上的所有点都在这个平面内（即直线在 或 经过直线）‎ 判断直线是否在平面内的依据 基本性质2‎ 经过不在同一条直线上的 ，有且只有一个平面（即 确定一个平面）‎ 确定平面及两个平面重合的依据 基本性质3‎ 如果不重合的两个平面有 公共点，那么它们有且只有一条过这个点的公共直线 判断两平面相交，线共点，点共线的依据 ‎2.平面基本性质的推论 推论1：经过一条直线和直线外的一点， 个平面.‎ 推论2：经过两条 直线，有且只有一个平面.‎ 推论3：经过两条 直线，有且只有一个平面.‎ 知识点二　共面与异面直线 ‎1.空间两直线的位置关系 位置关系 特点 共面 相交 同一平面内，有且只有 个公共点 平行 同一平面内， 公共点 异面直线 既不 又不 ‎ ‎2.点、线、面之间的关系的符号表示 点在直线上 ‎（或直线经过点）‎ 元素与集合间的关系 点在直线外 ‎（或直线不经过点）‎ 点在平面内 ‎（或平面经过点）‎ 点在平面外 ‎（或平面不经过点）‎ 直线在平面内 ‎（或平面经过直线）‎ 两个集合间的关系 直线与平面相交于点 直线与直线相交于点 4‎ 平面与平面相交于直线 ‎【归纳·升华、领悟】‎ ‎1.对异面直线的理解 ‎（1）异面直线的定义表明：异面直线不具备确定平面的条件.异面直线既不相交，也不平行. 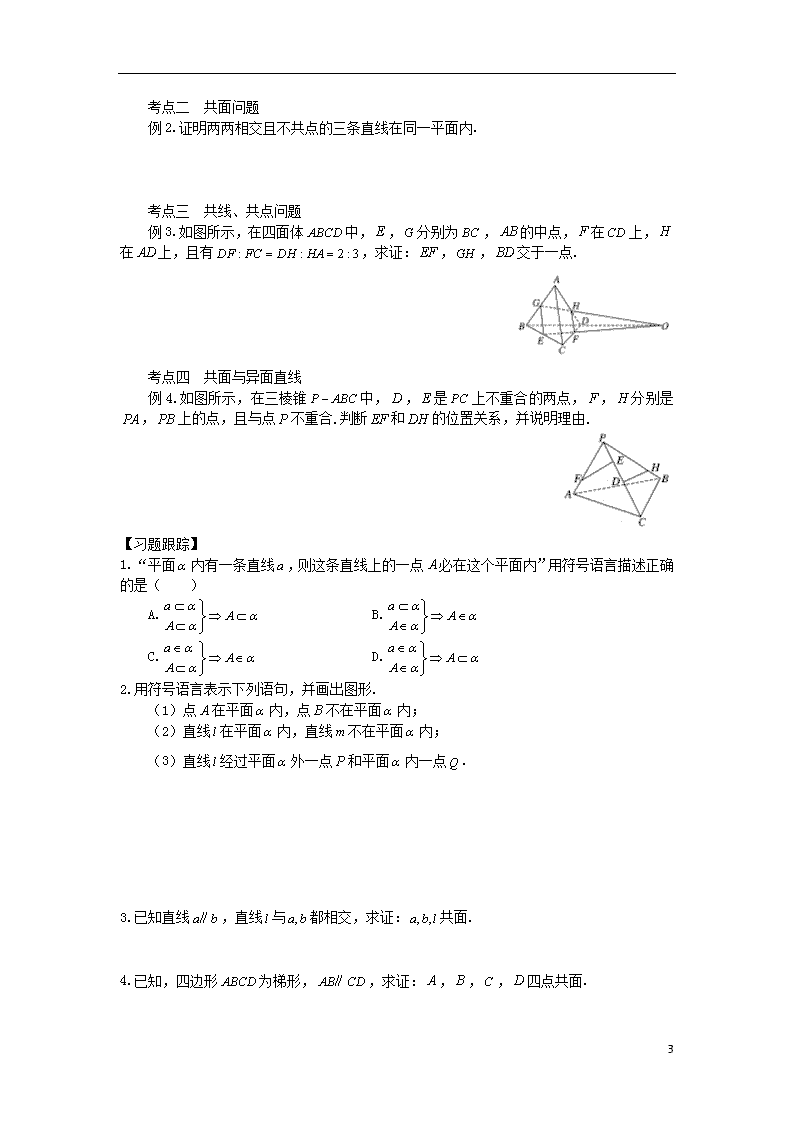‎ ‎（2）不能把异面直线误解为：分别在不同平面内的两条直线为异面直线.如图所示，虽然有，，即分别在两个不同的平面内，但是由于，所以与不是异面直线.‎ ‎2.从集合角度理解点、线、面之间的关系 ‎（1）直线可以看成无数个点组成的集合，故点与直线的关系是元素与集合的关系，用“”或“”表示；‎ ‎（2）平面也可以看成点集，故点与平面的关系也是元素与集合的关系，用“”或“”表示；‎ ‎（3）直线和平面都是点集，它们之间的关系可看成集合与集合的关系，故用“”或“”表示.‎ ‎【典型例题】‎ 考点一　用符号语言表示图形中元素的位置关系 例1.如图，用符号表示下列图形中点、直线、平面之间的位置关系.‎ ‎‎ 4‎ 考点二　共面问题 例2.证明两两相交且不共点的三条直线在同一平面内.‎ 考点三　共线、共点问题 例3.如图所示，在四面体中，，分别为，的中点，在上，在上，且有，求证：，，交于一点.‎ 考点四　共面与异面直线 例4.如图所示，在三棱锥中，，是上不重合的两点，，分别是，上的点，且与点不重合.判断和的位置关系，并说明理由.‎ ‎【习题跟踪】‎ ‎1.“平面内有一条直线，则这条直线上的一点必在这个平面内”用符号语言描述正确的是（　　）‎ A. B.‎ C. D.‎ ‎2.用符号语言表示下列语句，并画出图形.‎ ‎（1）点在平面内，点不在平面内；‎ ‎（2）直线在平面内，直线不在平面内；‎ ‎（3）直线经过平面外一点和平面内一点.‎ ‎3.已知直线，直线与都相交，求证：共面.‎ ‎4.已知，四边形为梯形，，求证：，，，四点共面.‎ 4‎ ‎5.已知：如图所示，平面、、满足，，，.‎ 求证：三线交于一点.‎ ‎6.如图所示，在正方体中，设线段与平面中，设线段与平面交于点，求证：，，三点共线.‎ ‎7.如图所示，在长方体中，与异面的是（　　）‎ A.AB B. ‎ C. D.‎ ‎8.如图，正方体中，判断下列直线的位置关系：‎ ‎①直线与直线的位置关系是 ；‎ ‎②直线与直线的位置关系是 ；‎ ‎③直线与直线的位置关系是 ；‎ ‎④直线与直线的位置关系是 .‎ ‎【方法·规律·小结】‎ ‎1.三种语言的相互转换是一种基本技能，要注意符号语言的意义；由符号语言画相应图形时，要注意实虚线.‎ ‎2.证明点线共面的主要依据是公理1，公理3‎ 证明点共线的依据是公理3，证明线共面的依据是公理1，一般是先定线、定面，再证其它的点、线在线上（面内）.‎ ‎3.判定两条直线的位置关系时.若要判定直线平行或相交可用平面几何中的定义和方法处理.判定异面直线的方法往往用定义和反证法.借助几何模型判定两直线的位置关系，也是常用的一种方法，更直观。‎ 4‎