人教A版高中数学2-1-2指数函数（2）教案新人教版必修1 3页

2.1.2（2）指数函数（教学设计） 教学目标 1.掌握指数函数的图象与性质，会求指数函数的定义域. 2. 通过指数函数的图象和性质的学习,培养学生观察,分析,归纳的能力,进一步体会数形结合的思想方法. 3. 通过对指数函数的研究,使学生能把握函数研究的基本方法,激发学生的学习兴趣. 教学重点和难点 重点：作指数函数的图像. 难 点：图像的平移变换. 教学过程 一、复习回顾，新课引入 1、完成下列表格： 1a  0 1a  图 象 定义域 值域 性质 （1）过定点 ， （2） （2） 二、师生互动，新课讲解： 例 1： 求下列函数的定义域： （1） 310 xy  ； （2） 1 0.8xy  ； （3） 4 1 3  xy ； （4） xy )2 1(1 变式训练 1：解下列指数不等式： （1） 2 32x  ；（2） 1( ) 162 x  ；（3） 2 13 27x   例 2：比较下列各题中两个数的大小： （1） 3.5 41.9 1.9， ； （2） 0.2 0.10.6 0.6 ， ； （3） 0.3 3.11.8 0.7， ． 解 （１）考察指数函数 1.9xy  ，由于底数1.9 1 ，所以指数函数 1.9xy  在 ( ) ，+ 上是增函数． ∵ 3.5 4 ，∴ 3.5 41.9 1.9< ． （2）考察指数函数 0.6xy  ，由于底数 0 0.6 1  ，所以指数函数 0.6xy  在 ( ) ，+ 上是减函数． ∵ 0.2 25x  0.2 0.1   ，∴ 0.2 0.10.6 0.6  ． （3）由指数函数的性质知 0.3 01.8 1.8 1  ， 3.1 00.7 0.7 1  ， 即 0.3 3.11.8 0.7 1>1， ，∴ 0.3 3.11.8 0.7 ． 变式训练 2：（1）已知 3 3 5 5 m n          ，试比较 m n与 的大小； （2）已知 0.5 64x  ，求实数 x 的取值范围． 解 （１）考察指数函数 3 5 x y      ，由于底数 30 15   ，所以指数函数 3 5 x y      在 ( ) ，+ 上是减函数． ∵ 3 3 5 5 m n          ，∴ m n ． （2）考察指数函数 1 2 x y      ，由于底数 10 12   ，所以指数函数 1 2 x y      在 ( ) ，+ 上是减函数． ∵ 10.5 2  ， 6 6 164 2 2       ， 0.5 64x  ，∴ 61 1 2 2 x           ， ∴ 6x   ，即 x 的取值范围是 ( , 6)  ． 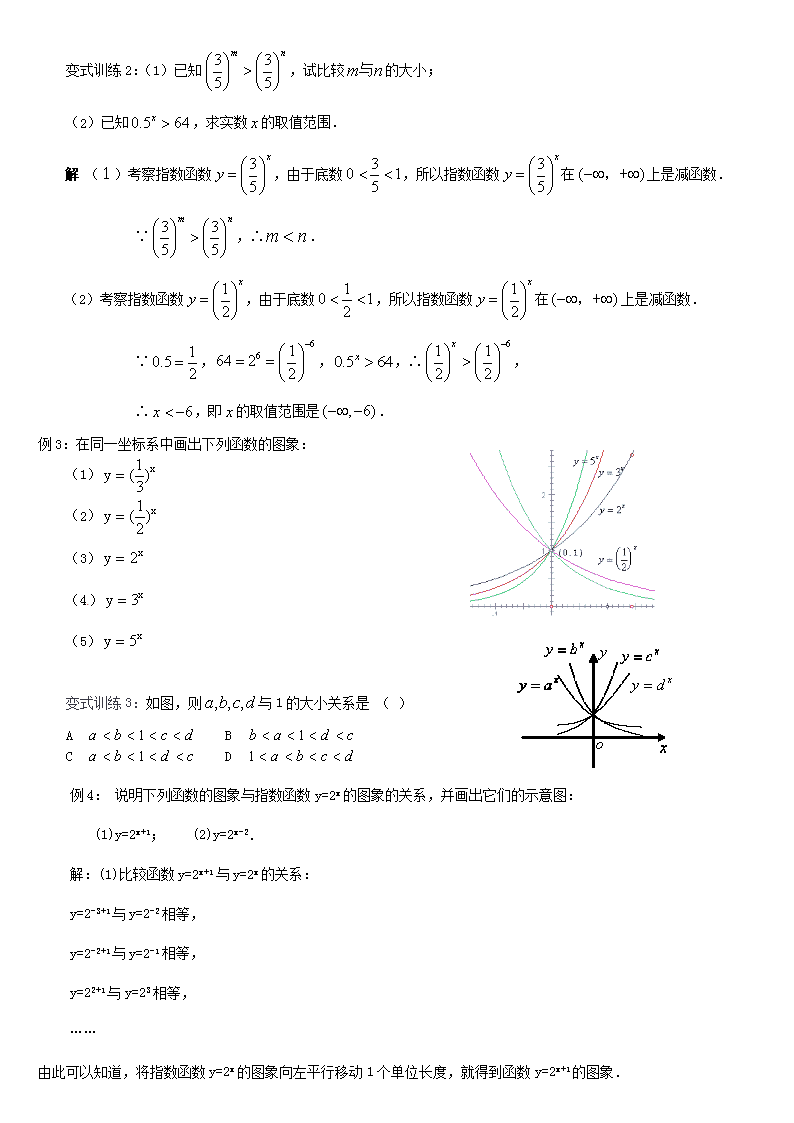例 3：在同一坐标系中画出下列函数的图象： （1） x)3 1(y  （2） x)2 1(y  （3） x2y  （4） x3y  （5） x5y  变式训练 3：如图，则 dcba ,,, 与 1 的大小关系是 （ ） A dcba  1 B cdab  1 C cdba  1 D dcba 1 例 4： 说明下列函数的图象与指数函数 y=2x 的图象的关系，并画出它们的示意图： (1)y=2x+1； (2)y=2x-2． 解：(1)比较函数 y=2x+1 与 y=2x 的关系： y=2-3+1 与 y=2-2 相等， y=2-2+1 与 y=2-1 相等， y=22+1 与 y=23 相等， …… 由此可以知道，将指数函数 y=2x 的图象向左平行移动 1 个单位长度，就得到函数 y=2x+1 的图象． （2)比较函数 y=2x-2 与 y=2x 的关系： y=2-1-2 与 y=2-3 相等， y=20-2 与y=2-2 相等， y=23-2 与 y=21 相等， 补充：图像平移变换： 左加右减，上加下减。 变式训练 4：作出下列函数的图像： （1） | |2 xy  ；（2） | 1|2 xy  三、课堂小结，巩固反思： 1、指数函数的单调性的应用。 2、指数不等式的解法-----同底化。 3、图像的平移变换。 四、布置作业： 1、(tb0114001)函数 y=3x 与 y=( 3 1 )x 的图象（B）。 （A）关于 x 轴对称 （B）关于 y 轴对称 （C）关于原点对称 （D）关于直线 y=x 对称 2、（课本 P59 习题 2 .1 A 组 NO：5） 3、（课本 P59 习题 2.1 A 组 NO：7） 4、作出函数 | 2|1( )3 xy  的图像， 并写出它的单调区间。 5、作出函数 | |2 xy  的图像，根据图像：（1）求出定义域，值域；（2）判断函数的奇偶性；（3）写出单调区间。 B 组： 1、（课本 P59 习题 2.1 B 组 NO：1） 2、（课本 P59 习题 2.1 B 组 NO：4） 3、函数 f(x)＝ax－b 的图像如图所示，其中 a，b 为常数，则下列 结论正确的是 ( D ) A．a>1，b<0 B．a>1，b>0 C．00 D．0