2019-2020学年高中数学课时作业11二项式系数的性质北师大版选修2-3 6页

课时作业(十一)‎ ‎1．在二项式(x2－)5的展开式中，含x4的项的系数是(　　)‎ A．－10　　　　　　　　　　 B．10‎ C．－5 D．5‎ 答案　B 解析　展开式的通项为Tr＋1＝C5r(x2)5－r·(－)r＝(－1)r·C5r·x10－3r，‎ 令10－3r＝4，∴r＝2，则x4的系数是(－1)2·C52＝10.故选B.‎ ‎2．(2x3－)10的展开式中的常数项是(　　)‎ A．210 B. C. 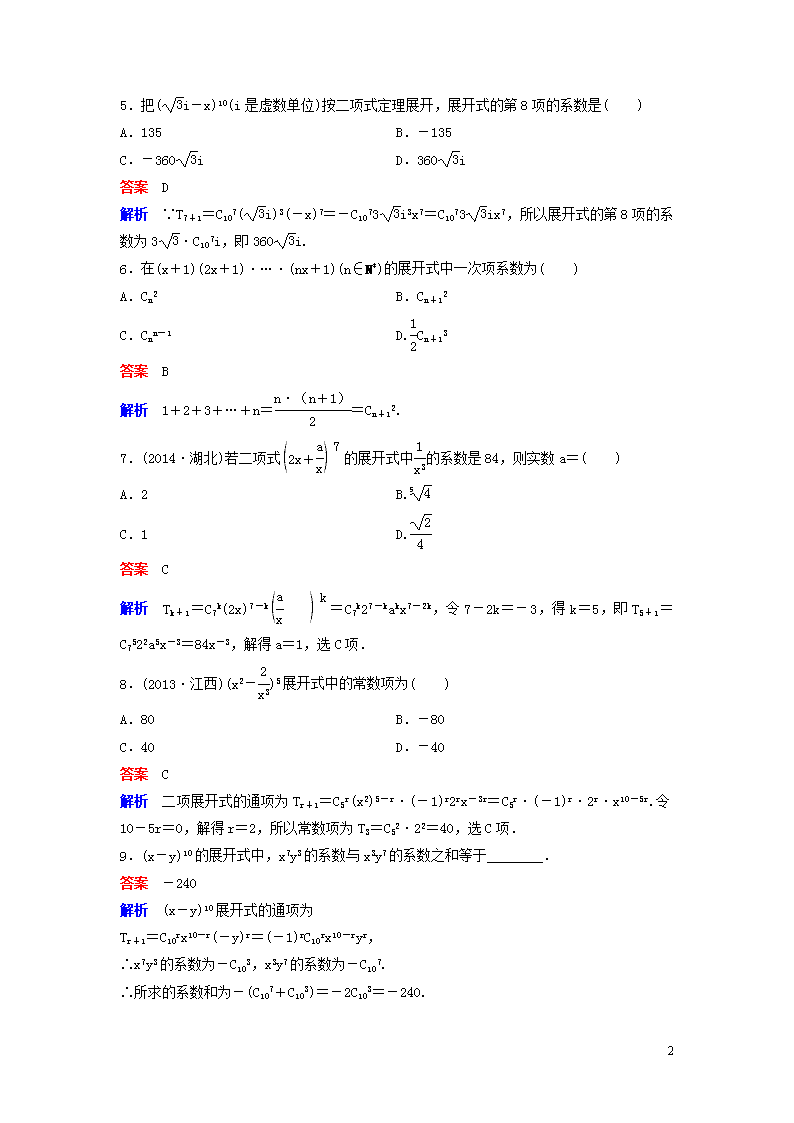D．－105‎ 答案　B ‎3．(2014·湖南)(x－2y)5的展开式中x2y3的系数是(　　)‎ A．－20 B．－5‎ C．5 D．20‎ 答案　A 解析　根据二项展开式的通项公式求解．‎ ‎(x－2y)5展开式的通项公式为Tr＋1＝C5r(x)5－r·(－2y)r＝C5r·()5－r·(－2)r·x5－r·yr.‎ 当r＝3时，C53()2·(－2)3＝－20.‎ ‎4．二项式(＋)24展开式中的整数项是(　　)‎ A．第15项 B．第14项 C．第13项 D．第12项 答案　A 解析　(＋)24展开式的通项为C24r()24－r·()r.要使其为整数，应使与都是整数，观察易知r＝14时＝2，＝2皆为整数，因此所求为第r＋1项，即第15项．‎ ‎5．把(i－x)10(i是虚数单位)按二项式定理展开，展开式的第8项的系数是(　　)‎ A．135 B．－135‎ 6‎ C．－360i D．360i 答案　D 解析　∵T7＋1＝C107(i)3(－x)7＝－C1073i3x7＝C1073ix7，所以展开式的第8项的系数为3·C107i，即360i.‎ ‎6．在(x＋1)(2x＋1)·…·(nx＋1)(n∈N*)的展开式中一次项系数为(　　)‎ A．Cn2　　　　　　　　　 B．Cn＋12‎ C．Cnn－1 D.Cn＋13‎ 答案　B 解析　1＋2＋3＋…＋n＝＝Cn＋12.‎ ‎7．(2014·湖北)若二项式的展开式中的系数是84，则实数a＝(　　)‎ A．2 B. C．1 D. 答案　C 解析　Tk＋1＝C7k(2x)7－k＝C7k27－kakx7－2k，令7－2k＝－3，得k＝5，即T5＋1＝C7522a5x－3＝84x－3，解得a＝1，选C项．‎ ‎8．(2013·江西)(x2－)5展开式中的常数项为(　　)‎ A．80 B．－80‎ C．40 D．－40‎ 答案　C 解析　二项展开式的通项为Tr＋1＝C5r(x2)5－r·(－1)r2rx－3r＝C5r·(－1)r·2r·x10－5r.令10－5r＝0，解得r＝2，所以常数项为T3＝C52·22＝40，选C项．‎ ‎9．(x－y)10的展开式中，x7y3的系数与x3y7的系数之和等于________．‎ 答案　－240‎ 解析　(x－y)10展开式的通项为 Tr＋1＝C10rx10－r(－y)r＝(－1)rC10rx10－ryr，‎ ‎∴x7y3的系数为－C103，x3y7的系数为－C107.‎ ‎∴所求的系数和为－(C107＋C103)＝－2C103＝－240.‎ ‎10．化简：(x－1)4＋4(x－1)3＋6(x－1)2＋4x－3的值为________．‎ 答案　x4‎ 解析　原式为 6‎ ‎(x－1)4＋4(x－1)3＋6(x－1)2＋4(x－1)＋1‎ ‎＝[(x－1)＋1]4＝x4.‎ ‎11．(x－1)－(x－1)2＋(x－1)3－(x－1)4＋(x－1)5的展开式中，x2的系数等于________．‎ 答案　－20‎ 解析　方法一　所给的代数式是五个二项式的代数和．因此所求的x2的系数就应该是这五个二项式的展开式中x2的系数的代数和，即－C20－C31－C42－C53＝－20.‎ 方法二　也可以利用等比数列求和公式，将原式化为＝.可以看出，所求的x2的系数就是(x－1)6中x3的系数，即为－C63＝－20.‎ ‎12．(＋)50的二项展开式中，整数项共有________项．‎ 答案　4‎ 解析　Tk＋1＝C50k()50－k·()k＝C50k·2.‎ 由0≤k≤50，且k∈N可知，当k＝2，8，14，20时，‎ 取整数，即展开式中有4项是整数项．‎ ‎13．在二项式(x＋)80的展开式中，系数为有理数的项共有多少项？‎ 解析　设系数为有理数的项为第k＋1项，‎ 即C80k(x)80－k()k＝240－×3C80kx80－k，‎ 因为系数为有理数，所以k应能被2整除．‎ 又因为k＝0，1，2，…，80，‎ 所以当k＝0，2，4，6，…，80时，满足条件，所以共有41项．‎ ‎14．求(x＋－1)5展开式中的常数项．‎ 解析　方法一　(x＋－1)5＝(x＋－1)(x＋－1)(x＋－1)(x＋－1)(x＋－1)．‎ 按多项式乘法的规律，常数可从五个因式中都选取－1相乘为(－1)5；若从五个因式中选定一因式取x，一因式取，另三个因式中取(－1)，为C51C41(－1)3；若从五个因式某两因式中取x，另两因式中取，余下一个因式中取－1，所得式为C52C32(－1)，所以常数项为 ‎(－1)5＋C51C41(－1)3＋C52C32(－1)＝－51.‎ 方法二　由于本题只有5次方，也可以直接展开，即 6‎ ‎[(x＋)－1]5＝(x＋)5－5(x＋)4＋10(x＋)3－10(x＋)2＋5(x＋)－1.‎ 由x＋的对称性知，只有在x＋的偶数次幂中的展开式中才会出现常数项且是各自的中间项，‎ ‎∴常数项为－5C42－10C21－1＝－51.‎ 方法三　∵(x＋－1)5＝[(x＋)－1]5，‎ ‎∴通项为Tr＋1＝C5r(x＋)5－r·(－1)r(0≤r≤5)．‎ 当r＝5时，T6＝C55(－1)5＝－1；‎ 当0≤r<5时，(x＋)5－r的通项为 T′k＋1＝C5－rkx5－r－k·()k ‎＝C5－rkx5－r－2k(0≤k≤5－r)．‎ ‎∵0≤r<5，且r∈Z，‎ ‎∴r只能取1或3相应的k值分别为2或1.‎ ‎∴常数项为C51C42(－1)＋C53C21(－1)3＋(－1)＝－51.‎ ‎15．(2015·衡水高二检测)在(2x2－)8的展开式中，求：‎ ‎(1)第5项的二项式系数及第5项的系数；‎ ‎(2)x2的系数．‎ 解析　(1)T5＝T4＋1＝C84(2x2)8－4(－)4‎ ‎＝C84·24·x.‎ 所以第5项的二项式系数是C84＝70，第5项的系数是C84·24＝1 120.‎ ‎(2)(2x2－)8的通项是Tk＋1＝‎ C8k(2x2)8－k(－)k＝(－1)kC8k·28－k·x16－k.‎ 根据题意得，16－k＝2，解得k＝6.‎ 因此，x2的系数是(－1)6C86·28－6＝112.‎ ‎16．在二项式(－)n的展开式中，前三项系数的绝对值成等差数列．‎ ‎(1)求展开式的第四项；‎ 6‎ ‎(2)求展开式的常数项．‎ 解析　Tk＋1＝Cnk()n－k(－)k ‎＝(－)kCnkxn－k，‎ 由前三项系数的绝对值成等差数列，‎ 得Cn0＋(－)2Cn2＝2×Cn1，‎ 解这个方程得n＝8或n＝1(舍去)．‎ ‎(1)展开式的第四项为T4＝(－)3C83x＝－7.‎ ‎(2)当－k＝0，即k＝4时，常数项为(－)4C84＝.‎ ‎►重点班选做题 ‎17．(1－x)4(1－)3的展开式中x2的系数是(　　)‎ A．－6 B．－3‎ C．0 D．3‎ 答案　A 解析　由于(1－x)4的通项为Tr＋1＝C4r(－x)r＝(－1)rC4rxr，(1－)3的通项为Tk＋1＝(－1)kC3kx，所以乘积中的x2项的系数为(1－x)4中的x2项的系数和x的系数分别乘(1－x)3中的常数项和x的系数再求和得到，即6×1＋(－4)×3＝6－12＝－6.‎ ‎18．(x＋)(2x－)5的展开式中各项系数的和为2，则该展开式中常数项为(　　)‎ A．－40 B．－20‎ C．20 D．40‎ 答案　D 解析　对于(x＋)(2x－)5，可令x＝1得1＋a＝2，故a＝1.(2x－)5的展开式的通项Tr＋1＝C5r(2x)5－r(－)r＝C5r25－r×(－1)r×x5－2r，要得到展开式的常数项，则x＋的x与(2x－)5展开式的相乘，x＋的与(2x－)5展开式的x相乘，故令5－2r＝－1，得r＝3.令5－2r＝1，得r＝2，从而可得常数项为C53×22×(－1)3＋C52×23×(－1)2＝40.‎ ‎19．若(cosφ＋x)5的展开式中x3的系数为2，则sin(2φ＋)＝________．‎ 6‎ 答案　－ 解析　由二项式定理，得x3的系数为C53cos2φ＝2，得cos2φ＝，故sin(2φ＋)＝cos2φ＝2cos2φ－1＝－.‎ ‎20．设二项式(x－)6(a>0)的展开式中x3的系数为A，常数项为B.若B＝4A，则a的值是________．‎ 答案　2‎ 解析　对于Tr＋1＝C6rx6－r()r＝C6r(－a)rx6－r，‎ B＝C64(－a)4，A＝C62(－a)2.∵B＝4A，a>0，∴a＝2.‎ 6‎