2021届高考数学一轮复习第三章三角函数与解三角形第5讲三角函数的图象与性质课件 42页

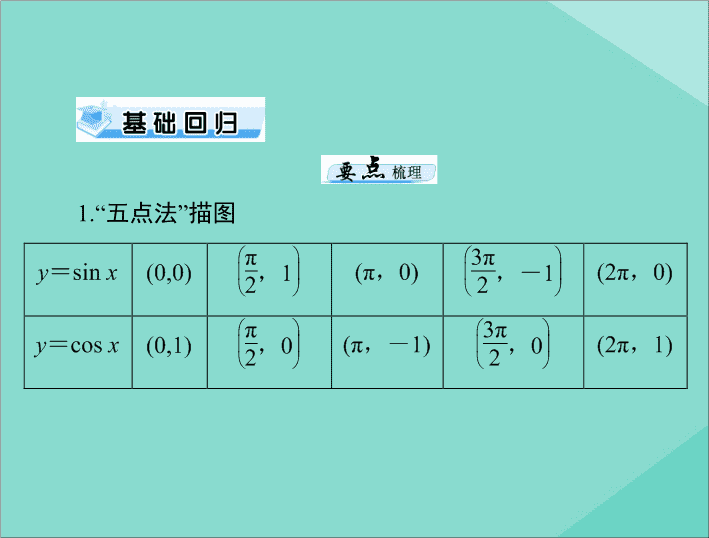
第 5 讲　三角函数的图象与性质 课标要求 考情风向标 1. 能画出 y ＝ sin x, y ＝ cos x, y ＝ tan x 的图象，了解三角函数的周 期性 . 2. 借助图象理解正弦函数、余弦 函数在 [0 ， 2π] ，正切函数在 上的性质 ( 如单调性、最 大和最小值、图象与 x 轴交点等 ) 1. 要熟记本节的基础知识，并会将 ωx ＋ φ 看作一个整体进行解题 . 2. 解题时要注意图象的应用，如利用 图 象求函数的最值、值域等 . 3. 注重三角函数的性质和三角恒等 变换的综合问题，这是近几年高考 的热点 . 4. 注 重函数与方程、转化与化归、数 形结合思想等数学思想方法的运用 1.“ 五点 法 ” 描图 函数 y ＝ sin x y ＝ cos x y ＝ tan x 定义域 R R 图象 值域 [ － 1,1] __________ R 2. 三角函数的图象和性质 [ － 1,1] ( 续表 ) π ( 续表 ) 偶 C 对任意的实数 x 都成立，则 ω 的最小值为 _______. 3. (2019 年北京 ) 函数 f ( x ) ＝ sin 2 2 x 的最小正周期是 ____. 数为 _______. 3 考点 1 三角函数的定义域和值域 最大值为 ( ) A.4 B.5 C.6 D.7 解析： f ( x ) ＝ 1 － 2sin 2 x ＋ 6sin x ∴ 当 sin x ＝ 1 时取最大值 5. 故选 B. 答案： B 答案： 1 答案： － 4 考点 2 三角函数的奇偶性、周期性与对称性 sin ωx ( ω >0) 两个相邻的极值点，则 ω ＝ ( ) 答案： A (2)(2015 年四川 ) 下列函数中，最小正周期为 π 且图象关于原 点对称的函数是 ( ) 且图象关于原点对称 . 故选 A. 方法二，逐项检验，但这类题 常常 采用排除法 . 很明显， C ， D 选项中的函数既不是奇函数也不是 偶函数，而 B 选项中的函数是偶函数，故均可排除 . 故选 A. 答案： A (3)(2014 年新课标 Ⅰ ) 在函数 ① y ＝ co s |2 x | ； ② y ＝ |cos x | ； 数为 ( ) A.①②③ C.②④ B.①③④ D.①③ 答案： A 答案： B 其中所有正确结论的编号是 ( ) A.①④ B.②③ C.①②③ D.①③④ 极小值点不确定，可能是 2 个也可能是 3 个， ② 不正确； 故选 D. 答案： D 【规律方法】 (1) 三角函数型奇偶性判断除可以借助定义 外，还可以借助其图象的性质，对 y ＝ A sin( ωx ＋ φ ) 代入 x ＝ 0 ， 若 y ＝ 0 ，则 y 为奇函数；若 y 为最大或最小值，则 y 为偶函数 . 若 y ＝ A sin( ωx ＋ φ ) 为奇函数，则 φ ＝ k π( k ∈ Z ) ；若 y ＝ A sin( ωx ＋ φ ) 考点 3 三角函数的单调性与最值 例 3 ： (1) (2015 年新课标 Ⅰ ) 函数 f ( x ) ＝ cos( ωx ＋ φ ) 的部分图 ) 象如图 3-5-1 ，则 f ( x ) 的单调递减区间为 ( 图 3-5-1 答案： D 答案： D 【 跟踪训练 】 A. f ( x ) ＝ |cos 2 x | B. f ( x ) ＝ |sin 2 x | C. f ( x ) ＝ cos | x | D. f ( x ) ＝ sin | x | 答案： A 答案： A 难点突破 ⊙ 三角函数中参数问题的讨论 且只有一解，则正数 ω 的最大值是 ( ) A.8 C.6 B.7 D.5 解析： sin ωx ＋ 1 ＝ 0 可变为 sin ωx ＝－ 1 ， 图 3-5-2 答案： B A.11 C.7 B.9 D.5 答案： B 【 跟踪训练 】 答案： 9 1. 讨论三角函数性质，应先把函数式化成 y ＝ A sin( ωx ＋ φ ) ( ω ＞ 0) 的形式 . 2. 函数 y ＝ A sin( ωx ＋ φ ) 和 y ＝ A cos( ωx ＋ φ ) 的最小正周期为 3. 对于函数的性质 ( 定义域、值域、单调 性、对称性、最值 等 ) 可以通过换元的方法令 t ＝ ωx ＋ φ ，将其转化为研究 y ＝ sin t 的性质 . 4. 闭区间上最值或值域问题，首先要在定义域基础上分析 单调性，含参数的最值问题，要讨论参数对最值的影响 . 5. 要注意求函数 y ＝ A sin( ωx ＋ φ ) 的单调区间时 A 和 ω 的符 号，尽量化成 ω ＞ 0 的情况，避免出现增减区间的混淆 .