福建省莆田市2019届高三第二次质量检测（A卷）（5月） 数学（理）（PDF版） 15页

- 1 - 2019 年莆田市高中毕业班第二次质量检测试卷(A 卷) 理科数学 本试卷共 5 页．满分 150 分．考试时间 120 分钟． 注意事项： 1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上． 2.考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书 写的答案无效．在草稿纸、试题卷上答题无效． 3.选择题答案使用 2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用 0.5 毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚． 4.保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回． 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符合题 目要求的. 1.设全集  8U x xN ≤ ，集合  1,3,7A  ,  2,3,8B  , 则 U ABð A.  2,3,4,5,6,8 B.  2,8 C.  1,7 D.  3 2.已知 iza( 0)a  ，且 2z  ，则 z  A. 1i B. 1i C. 3i D. 3i 3.执行如右图所示的程序框图，最后输出结果为 A. 16 B. 31 C. 32 D. 62 4. 函数   sine1xfx在 ,  上的图像大致为 A B C D 5.从 4 位女生， 3位男生中选 3人参加科技比赛，则至多有 2 位女生入选的方法种数为 A. 30 B. 31 C. 185 D. 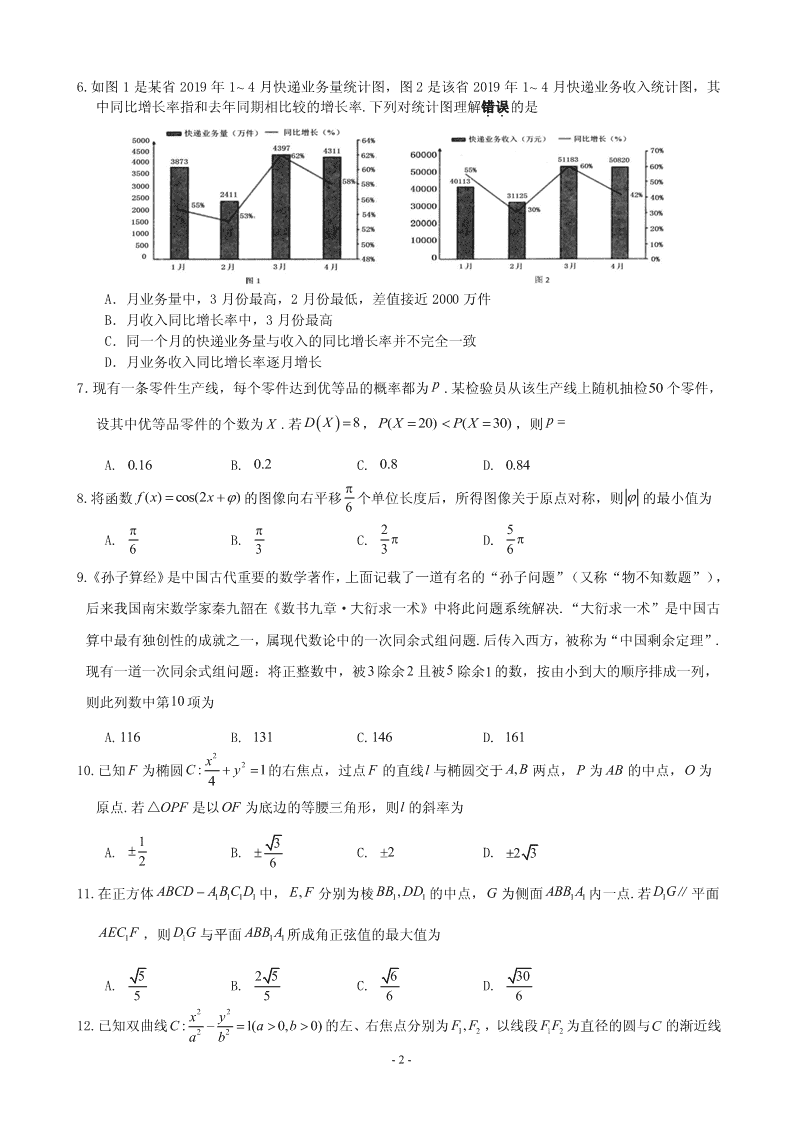186 - 2 - 6.如图 1 是某省 2019 年 1~ 4 月快递业务量统计图，图 2 是该省 2019 年 1 4 月快递业务收入统计图，其 中同比增长率指和去年同期相比较的增长率.下列对统计图理解错误．．的是 A．月业务量中，3 月份最高，2 月份最低，差值接近 2000 万件 B．月收入同比增长率中，3 月份最高 C．同一个月的快递业务量与收入的同比增长率并不完全一致 D．月业务收入同比增长率逐月增长 7．现有一条零件生产线，每个零件达到优等品的概率都为 p .某检验员从该生产线上随机抽检50 个零件， 设其中优等品零件的个数为 X .若   8DX  ， ( 20)PX ( 30)PX，则 p  A. 0.16 B. 0.2 C. 0.8 D. 0.84 8.将函数 ( ) cos(2 )f x x 的图像向右平移 6  个单位长度后，所得图像关于原点对称，则  的最小值为 A. 6  B. 3  C. 2 3  D. 5 6  9.《孙子算经》是中国古代重要的数学著作，上面记载了一道有名的“孙子问题”（又称“物不知数题”）， 后来我国南宋数学家秦九韶在《数书九章·大衍求一术》中将此问题系统解决.“大衍求一术”是中国古 算中最有独创性的成就之一，属现代数论中的一次同余式组问题.后传入西方，被称为“中国剩余定理”. 现有一道一次同余式组问题：将正整数中，被 3除余 2 且被5 除余1的数，按由小到大的顺序排成一列， 则此列数中第10项为 A.116 B. 131 C.146 D. 161 10.已知 F 为椭圆 2 2:14 xCy的右焦点，过点 F 的直线l 与椭圆交于 ,AB两点， P 为 AB 的中点，O 为 原点.若 OPF△ 是以 OF 为底边的等腰三角形，则l 的斜率为 A. 1 2 B. 3 6 C. 2 D. 23 11.在正方体 1 1 1 1ABCD A B C D 中， ,EF分别为棱 11,BB DD 的中点，G 为侧面 11ABB A 内一点.若 1DG∥平面 1AEC F ，则 1DG与平面 11ABB A 所成角正弦值的最大值为 A. 5 5 B. 25 5 C. 6 6 D. 30 6 12.已知双曲线 22 221( 0, 0: )xy ababC     的左、右焦点分别为 12,FF，以线段 12FF 为直径的圆与C 的渐近线 - 3 - 在第一象限的交点为 P ，且 122PF PF b.设 C 的离心率为 e ，则 2e = A. 13 2  B. 15 2  C. 3 D. 5 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 13.若向量    2,3 , 4,AB BC m   ，且 ,,A B C 三点共线，则 AB BC  ________. 14.若 ,xy满足约束条件 1, 1, 2 0, y yx xy      ≥ ≤ ≤ 则 22z x y的最小值是________. 15.已知 ,abR ,且 0.a  函数     2 2 , , 2 +1 , . x x x x a fx a x a x a      ≥ 若方程  f x b 至多有两个不等实数根，则 a 的取值范围为________. 16.对于 *,mnN ,数列 na 都有 mnaatmn   （t 为常数）成立，则称数列 na 具有性质 ()Rt .若数列 na 的 通项公式为 2 na n an，且具有性质 (10)R ，则实数 a 的取值范围是________. 三、解答题：共 70 分.解答题应写出文字说明、证明过程或演算步骤.第 17～21 题为必考题，每个试题考 生都必须作答.第 22，23 题为选考题，考生根据要求作答. （一）必考题 60 分. 17.（12 分） ABC△ 的内角 ,,A B C 的对边分别是 ,,abc.已知 cos sinb a C c A. （1）求 A ； （2）若 AC 边上的中线 BD 的长为 2 ，求 ABC△ 面积的最大值． 18.（12 分） 如图，以 1 1 1, , , , ,A B C A B C 为顶点的五面体中， 1 1 1AA BB CC∥ ∥ , 1CC  平面 ABC , 5AB BC， 1 1 122AA BB CC AC    ， F 是 AC 的中点. （1）求证： 1AC  平面 1BA F ； （2）求二面角 11B A F B的余弦值. 19. （12 分） - 4 - 某芯片公司为制定下一年的研发投入计划，需了解年研发资金投入量 x （单位：亿元）对年销售额 y（单位：亿元）的影响.该公司对历史数据进行对比分析，建 立了两个函数模型:① 2yx ，② e xty   ，其中 , , ,t   均为常数， e为自然对数的底数． 现该公司收集了近 12 年的年研发资金投入量 ix 和年销售 额 iy 的数据， 1,2, ,12i  ，并对这些数据作了初步处理，得 到了右侧的散点图及一些统计量的值． 令 2 ,iiux lniivy ( 1,2, ,12)i  ，经计算得如下数据： （1）设  iu 和 iy 的相关系数为 1r ， ix 和 iv 的相关系数为 2r ，请从相关系数的角度，选择一个拟 合程度更好的模型； （2）（i）根据（1）的选择及表中数据，建立 y 关于 x 的回归方程（系数精确到 0.01）； （ii）若下一年销售额 y 需达到 90 亿元，预测下一年的研发资金投入量x 是多少亿元？ 附：①相关系数 1 22 11 ( )( ) ( ) ( ) n ii i nn ii ii x x y y r x x y y        ， 回归直线 ˆy a bx 中斜率和截距的最小二乘估计公式分别为： 1 2 1 ( )( ) () n ii i n i i x x y y b xx        ， a y bx ； ② 参考数据： 308 4 77 ， 90 9.4868 ， 4.4998e 90 ． x y 12 2 1 ()i i xx   12 2 1 ()i i yy   u v 20 66 770 200 460 4.20 12 2 1 ()i i uu   12 1 ( )( )ii i u u y y   12 2 1 ()i i vv   12 1 ( )( )ii i x x v v   3125000 21500 0.308 14 - 5 - 20. （12 分） 已知抛物线  2: 2 0C x py p的焦点为 F ，准线为 l ，若点 P 在C 上，点 E 在l 上，且 PEF△ 是周长 为12的正三角形． （1）求 C 的方程； （2）过点 F 的直线与抛物线相交于 ,AB两点，抛物线在点 A 处的切线与l 交于点 N ，求 ABN△ 面积的 最小值. 21．（12 分） 已知函数   12e lnxf x a x x bx   的导函数为  fx ，且    1 2 1ff  . （1）求 a 的值； （2）若  fx有唯一极值点，且极值为 0 ，求 b 的值. (二)选考题:共 10 分.请考生在第 22、23 题中任选一题作答.注意:只能做所选定的题目,如果多做,则按所 做第一个题目计分,作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑. 22.[选修 4-4:坐标系与参数方程](10 分) 在直角坐标系 xOy 中，曲线 1C 的参数方程为 cos , 3sin x y     （ 为参数）.以坐标原点为极点，以 x 轴的 正半轴为极轴，建立极坐标系，曲线 2C 的极坐标方程为 sin( ) 2 24 . (1)写出 1C 的普通方程和 2C 的直角坐标方程； (2)设点 P 在 1C 上，点 Q 在 2C 上，求 PQ 的最小值及此时 P 的直角坐标. 23.[选修 4-5:不等式选讲](10 分) 已知函数   2f x x a a   . (1)若不等式   6fx≤ 的解集为 | 1 3xx ≤ ≤ ，求 a 的值； (2)设函数   21g x x.若     3f x g x ≤ ，求 a 的取值范围. - 6 - 2019 年莆田市高中毕业班第二次质量检测试卷(A 卷) 理科数学参考答案及评分细则 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内 容比照评分标准制定相应的评分细则. 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度， 可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答 有较严重的错误，就不再给分. 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数. 4．只给整数分数．选择题和填空题不给中间分. 一、选择题：本大题考查基础知识和基本运算.每小题 5 分，满分 60 分. 1．B 2.D 3.B 4.A 5.B 6.D 7．C 8.A 9.C 10.A 11.D 12.B 二、填空题：本大题考查基础知识和基本运算.每小题 5 分，满分 20 分. 13． 26 14. 1 2 15.  1,0 16. 7, . 三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤. 17.本小题主要考查正弦定理、三角形的面积公式、两角和与差的三角函数公式、诱导公式等基础知识， 考查推理论证能力和运算求解能力，考查函数与方程思想、化归与转化思想，考查逻辑推理、数学运 算等核心素养，体现基础性、综合性.满分 12 分. 解：(1)因为 cos sinb a C c A, 所以由正弦定理得， sin sin cos sin sinB A C C A, ................... 1 分 因为 B A C    , 代入得 sin( ) sin cos sin sinA C A C A C     , 所以 sin( ) sin cos sin sinA C A C A C   , ............................. 2 分 即 sin cos cos sin sin cos sin sinA C A C A C A C   , ...................... 3 分 所以 cos sin sin sinA C A C .......................................... 4 分 - 7 - 因为 sin 0C  , 所以 cos sinAA , .............................................. 5 分 又因为 A 为三角形内角， 所以 4A  . ..................................................... 6 分 （2）因为 BD 为边 AC 上的中线, 所以 2ABC ABDSS△ △ , ............................................. 7 分 设 ABD ,则 3 4ADB     .由正弦定理得， sin sin 4 BDAD  = 2 2 sin ， 32 2 sin( )4AB    , ................... 8 分 则 1 sin24ABDS AD AB     ....................................... 9 分 32 2 sin sin( )4     22sin +2sin cos    1+ sin2 cos2 1+ 2 sin(2 )4  , ...................................... 10 分 因为 30, 4  , 所以当 3 8  时， ABD△ 面积的最大值为12 , .................. 11 分 所以 ABC△ 面积的最大值为 2 2 2 . ............................... 12 分 - 8 - 18.本小题主要考查直线与平面垂直的判定与性质、二面角、空间向量等基础知识，考查空间想象能力、 推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想，考查直观想象、逻辑推理、数 学运算等核心素养，体现基础性、综合性. 满分 12 分. 解：（1）因为 1CC  平面 ABC ， BF  平面 ，所以 1CC BF . 因为 5AB BC， F 是 AC 的中点， 所以 BF AC . .................................................. 1 分 又 1CC AC C ， 所以 11BF AAC C 平面 ，从而 1BF AC . ............................ 2 分 因为 1CC  平面 ABC ，且 1 1 1 1,AA CC AA CC∥ ， 所以四边形 11AAC C 为直角梯形. 又 F 是 AC 的中点， 1122AA CC AC   ， 所以 1A AF△ 与 1ACC△ 均为等腰直角三角形， 所以 1145A FA C AC     . ....................................... 3 分 设 11A F AC D ，则 90ADF   ， 所以 11A F AC . ................................................. 4 分 又 1BF A F F ， 1,BF A F  平面 1BA F ， 所以 1AC  平面 . ............................................ 5 分 （2）由（1）知 11BF ACC A 平面 .设 11AC 的中点为 E ，连接 EF ， 则 EF ∥ 1CC ，从而 EF AC . 以 F 为原点， ,,FA FE FB分别为 x 轴， y 轴， z 轴 正方向建立如图所示空间直角坐标系. - 9 - 由题意得，          1 1 10,0,0 , 1,1,0 , 0,2,2 , 1,0,0 , 1,2,0 ,F A B A C  ................................................................ 6 分 则 1 1 1(0,2,2), (1,1,0), ( 2,2,0),FB FA AC    .......................... 7 分 设平面 11A B F 的法向量为 m ( , , )x y z ， 由 1 1 0, 0, FB FA    m m 得 2 2 0, 0, yz xy    ...................................... 8 分 令 1y  ，得 1, 1xz， 所以 m (1, 1,1) 为平面 11A B F 的一个法向量. ........................ 9 分 因为 1AC  平面 1BA F ， 所以 1 ( 2,2,0)AC  为平面 1BA F 的一个法向量. ...................... 10 分 因为    1 1 1 1 2 1 2 6cos , 33 2 2 AC AC AC          m m m ， .............. 11 分 且由图可知二面角 1 1 1B AC C为锐角， 所以二面角 1 1 1B AC C的余弦值为 6 .3 ........................... 12 分 19. 本小题主要考查回归分析等基础知识,考查数据处理能力、运算求解能力、抽象概括能力及应用意识, 考查统计与概率思想、分类与整合思想,考查数学抽象、数学运算、数学建模、数据分析等核心素养, 体现基础性、综合性与应用性．满分 12 分． 解：（1） 12 1 1 12 12 22 11 ( )( ) ( ) ( ) ii i ii ii u u y y r u u y y        21500 21500 43 0.8625000 503125000 200      ， .... 2 分 12 1 2 12 12 22 11 ( )( ) ( ) ( ) ii i ii ii x x v v r x x v v        14 14 10 0.9177 0.2 11770 0.308     ， ....... 4 分 则 12rr ，因此从相关系数的角度，模型 e xty   的拟合程度更好．.... 5 分 - 10 - （2）（i）先建立 v 关于 x 的线性回归方程. 由 e xty   ，得 ln y t x ，即 =v t x ． ......................... 6 分 由于 12 1 12 2 1 ( )( ) 14 0.018770() ii i i i x x v v xx           ， ........................... 8 分 4.20 0.018 20 3.84,t v x      ................................. 9 分 所以 v 关于 x 的线性回归方程为 0.02 3.84vx， 所以 ˆln 0.02 3.84yx，则 0.02 3.84ˆ e.xy  ........................... 10 分 （ii）下一年销售额 y 需达到 90 亿元，即 90y  ， 代入 0.02 3.84ˆ e xy  得， 0.02 3.8490 e x ， 又 4.4998e 90 ，所以 4.4998 0.02 3.84x，......................... 11 分 所以 4.4998 3.84 32.990.02x  ， 所以预测下一年的研发资金投入量约是32.99亿元................... 12 分 20.本小题主要考查抛物线的定义、抛物线的标准方程、直线与抛物线的位置关系、导数几何意义等基础 知识，考查推理论证能力、运算求解能力，考查函数与方程思想、化归与转化思想、数形结合思想 等，考查数学运算、直观想象、逻辑推理等核心素养，体现基础性、综合性与应用性.满分 12 分. 解：（1）由 PEF△ 是周长为 12 的等边三角形，得 =4PE PF EF， - 11 - 又由抛物线的定义可得 PE l . .................................... 1 分 设准线 l 与 y 轴交于 D ，则 PE DF∥ ，从而 60PEF EFD     ． ...... 2 分 在 EDFRt△ 中， 1cos 4 22DF EF EFD      ，即 2p  . .......... 3 分 所以抛物线 C 的方程为 2 4xy ..................................... 4 分 （2）依题意可知，直线 l 的斜率存在，故设直线 的方程为： 1y kx， 联立 2 4, 1, xy y kx     消去 y 可得， 2 4 4 0x kx   . 设    1 1 2 2, , ,A x y B x y ，则 1 2 1 24 , 4x x k x x    . ........................ 5 分 所以 2 121AB k x x    22 1 2 1 214k x x x x    221 16 16kk    241 k. ............................................. 6 分 由 2 4 xy  ，得 2 xy  ， 所以过 A 点的切线方程为  1 112 xy y x x   ， ......................... 7 分 又 2 1 1 4 xy  ， 所以切线方程可化为 2 11 24 xxyx   . .................................. 8 分 令 1y  ，可得 2 1 1 1 1 1 14 22 2 x yxkx x      , - 12 - 所以点 (2 , 1)Nk , ................................................. 9 分. 所以点 N 到直线 l 的距离 2 2 2 22 21 1 k dk k      ， .................... 10 分 所以 231 4 ( 1) 42ABNS AB d k   △ ≥ ，当 0k  时，等号成立. .......... 11 分 所以 ABN△ 面积的最小值为 4. .................................... 12 分 21.本小题主要考查函数的求导法则、函数的极值点与极值的概念等基础知识，考查推理论证能力、运算 求解能力与创新意识，考查函数与方程思想、化归与转化思想、数形结合思想、分类与整合思想，考 查数学抽象、直观想象、数学运算、逻辑推理等核心素养,体现综合性、应用性与创新性．满分 12 分． 解：（1）因为   12e lnxf x a x x bx   ， 所以   1e ln 1 2xf x a x bx     ， ................................ 1 分 所以  1f a b，  1 1 2f a b    . ................................ 2 分 又因为    1 2 1ff  ， 所以 1 2 2 2a b a b    ， ......................................... 3 分 解得 1a  . 所以 a 的值为1. ................................................. 4 分 （2）由（1）可得，   12e lnxf x x x bx   ，   1e ln 1 2xf x x bx     . 设  fx唯一极值点为 0x ，则     0 0 1 2 0 0 0 0 1 0 0 0 e ln 0 e ln 1 2 0 x x f x x x bx f x x bx              ， ① ，② .... 5 分 由② 0x① 2 得，   0 1 0 0 0 02 e ln 0xx x x x    .   ............... 6 分 令     12 e lnxF x x x x x    ，则     11 e lnxF x x x    ， 所以   1 1exF x x x   . - 13 - 又  Fx 在  0, 上单调递增，且  10F  ， ....................... 7 分 所以当  0,1x 时，   0Fx  ，从而  Fx 单调递减， 当  1,x  时，   0Fx  ，从而  Fx 单调递增， 故    10F x F≥ ，从而  Fx在 上单调递增， ............... 8 分 又因为  10F  ， 所以 0 1x  . ................................................... 9 分 代入①可得， 1b  . ........................................... 10 分 当 时，   12e lnxf x x x x   ，   1e ln 1 2xf x x x     ， 因为 1x  是   的唯一零点，且  10f  ，  10f   ， ................ 11 分 又   1 1 1 1 e 1 1 1 1e 2e e 2e e e 2 e e 2 0f              ，   34 e ln 4 1 8 0f       ， 所以 1x  是  fx唯一极值点，且极值为 0 ，满足题意. 所以 . .................................................. 12 分 22.选修 4-4：极坐标与参数方程 本小题主要考查直角坐标与极坐标互化、椭圆的参数方程、直线与椭圆的位置关系等基础知识,考查 运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,考查数学运算核心素养等，体 现基础性与综合性.满分 10 分. 解：（1）由曲线 1C 的参数方程 cos , 3sin x y     （ 为参数）消去参数得， 2 2 2 2cos sin 13 yx     ， 即 1C 的普通方程为： 2 2 13 yx . ................................... 2 分 - 14 - 曲线 2C 的极坐标方程为 sin( ) 2 24 可化为： 22( sin cos ) 2 222  . ................................... .3 分 由 cos , sinxy   ,可得 2C 的直角坐标方程为直线 40xy   . .... .5 分 （2）设  cos , 3sinP , .......................................... 6 分 则点 P 到直线 的距离为 cos 3 sin 4 2 d   ................ 7 分 2cos( ) 43 . 2    .................. 8 分 当 cos( ) 13    时, PQ 的最小值为 2, .......................... 9 分 此时可取 2 3  ,故 13,22P ． ................................ 10 分 23.选修 4-5：不等式选讲 本小题主要考查绝对值不等式,考查运算求解能力,考查分类与整合思想、化归与转化思想,考查数学 运算、逻辑推理等核心素养等，体现基础性与综合性.满分 10 分. 解：（1）因为   2f x x a a   , ( ) 6fx≤ , 所以| 2 | 6x a a≤ , ........................................... 1 分 即| 2 | 6x a a≤ , 所以  6 2 6a x a a   ≤ ≤ ,....................................... 2 分 解得 33ax ≤ ≤ , .............................................. 3 分 因为不等式   6fx 的解集为 | 1 3xx ≤ ≤ , 所以 31a    ,即 2a  . .................................. 5 分 （2）因为   21g x x, 所以 ( ) ( ) | 2 | | 2 1| | 1|f x g x x a x a a a       ≤ ,. .................. 6 分 当且仅当 (2 )(2 1) 0x a x≥ 时等号成立. ........................ 7 分 - 15 - 因为 ( ) ( ) 3f x g x ≤ 恒成立,所以 13aa≤ , 即 13aa≤ ① ...................................... 8 分 当 1a≤ 时,①等价于13aa≤ ，成立. 当 1a  时,①等价于 13aa≤ ，解得12a ≤ . ................... 9 分 综上所述 a 的取值范围是  ,2 ． .......................... 10 分