高考数学模拟试卷 (14) 13页

- 1 - 岳阳市一中 2018 届高三 5 月第一次模拟 数学试题（理科）(14) 第Ⅰ卷（共 60 分） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1．已知i 为虚数单位，若复数 z 满足 5 i1 2i z  ，则 z  （ ） A．1 i B． 1 i  C．1 2i D．1 2i 2．已知集合  2 1A y y x   ，   2ln 2B x y x x   ，则  A B R Ið （ ） A． 10, 2     B．  1,0 ,2     U C．  1,0 ,2     U D． 10, 2      3．将棱长相等的正方体按下图所示的形状摆放，从上往下依次为第 1 层，第 2 层，第 3 层，…， 则第 2018 层正方体的个数共有（ ） A．2018 B．4028 C．2037171 D．2009010 4．已知 2sin 6 3       ，那么 cos2 3sin 2   （ ） A．10 9 B． 10 9  C． 5 9  D． 5 9 5．元代数学家朱世杰的数学名著《算术启蒙》是中国古代代数学的通论，其中关于“松竹并 生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等.下图是源于其思 想的一个程序图，若 32a  ， 12b  ，则输出的 n  （ ） - 2 - A． 3 B．4 C．5 D．6 6．已知函数   22018tan1 x x mf x x xm     0, 1m m  ，若  1 3f  ，则  1f  等于 （ ） A．-3 B．-1 C．3 D．0 7．设抛物线 2 4y x 上一点 P 到 y 轴的距离为 1d ，到直线 :3 4 12 0l x y   的距离为 2d ， 则 1 2d d 的最小值为（ ） A．2 B． 15 3 C．16 3 D．3 8．已知函数    2cos 3 3 2f x x         ，若 ,6 12x        ，  f x 的图象恒在直 线 3y  的上方，则 的取值范围是（ ） A． ,12 2       B． ,6 3       C． 0, 4      D． ,6 3      9．岳阳高铁站 1B 进站口有 3 个闸机检票通道口，高考完后某班 3 个同学从该检票进站到外地 旅游，如果同一个人进的闸机检票通道口选法不同，或几个人进同一个闸机检票通道口但次 序不同，都视为不同的进站方式，那么这 3 个同学的不同进站方式有（ ）种。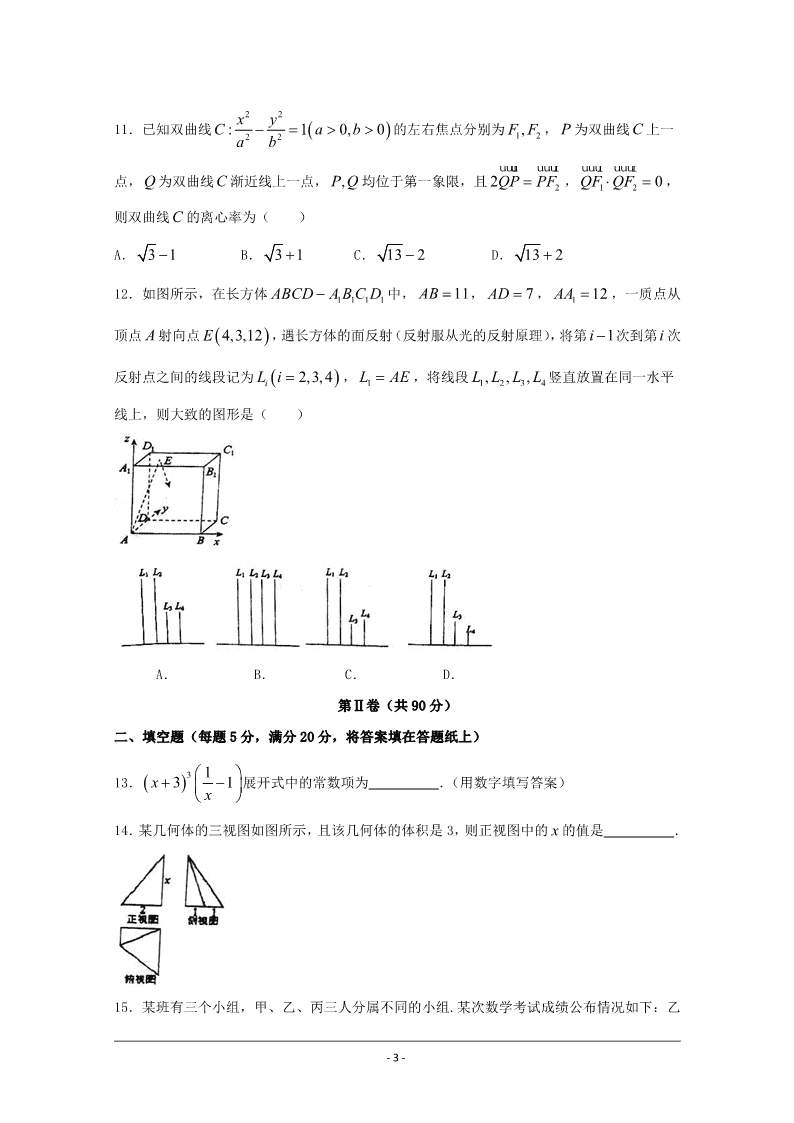 A．24 B．36 C．42 D．60 10．设点 O 在 ABC 的外部，且 2 3 5 0OA OB OC   uur uuur uuur r ，则 :ABC OBCS S   （ ） A． 2 :1 B．3:1 C．3: 2 D． 4 :1 - 3 - 11．已知双曲线   2 2 2 2: 1 0, 0x yC a ba b     的左右焦点分别为 1 2,F F ， P 为双曲线C 上一 点， Q 为双曲线C 渐近线上一点， ,P Q 均位于第一象限，且 22QP PF uuur uuur ， 1 2 0QF QF  uuur uuur ， 则双曲线 C 的离心率为（ ） A． 3 1 B． 3 1 C． 13 2 D． 13 2 12．如图所示，在长方体 1 1 1 1ABCD A B C D 中， 11AB  ， 7AD  ， 1 12AA  ，一质点从 顶点 A 射向点  4,3,12E ，遇长方体的面反射（反射服从光的反射原理），将第 1i  次到第i 次 反射点之间的线段记为  2,3,4iL i  ， 1L AE ，将线段 1 2 3 4, , ,L L L L 竖直放置在同一水平 线上，则大致的图形是（ ） A． B． C． D． 第Ⅱ卷（共 90 分） 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13．  3 13 1x x      展开式中的常数项为 ．（用数字填写答案） 14．某几何体的三视图如图所示，且该几何体的体积是 3，则正视图中的 x 的值是 ． 15．某班有三个小组，甲、乙、丙三人分属不同的小组.某次数学考试成绩公布情况如下：乙 - 4 - 和三人中的第 3 小组那位不一样，丙比三人中第 1 小组的那位的成绩低，三人中第 3 小组的 那位比甲分数高.将甲、乙、丙三人按数学成绩由高到低排列为 ． 16．在 ABC 中，角 A B C、 、 所对应的边分别为 a b c、 、 ，若 1bc  ， 2 cos 0b c A  ， 则当角 B 取得最大值时，三角形的内切圆的半径 r 为 ． 三、解答题 （本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤．） 17． 已知数列 na 的首项 1 1a  ，其前 n 项和为 nS ，且对任意正整数 n ，有 , ,n nn a S 成等差 数列. （1）求证：数列 2nS n  成等比数列； （2）设 n nb na ，求数列 nb 前 n 项和 nT . 18． 如图，四棱锥 S ABCD 的底面是平行四边形， DA DS ， BA BS . （1）求异面直线 SA 与 BD 所成的角； （2）若 DA DS ， 60ABS   ， BA BS BD  ，求二面角 D SC B  的余弦值. 19． 随着电商的快速发展，快递业突飞猛进，到目前，中国拥有世界上最大的快递市场.某 快递公司收取快递费用的标准是：重量不超过1kg 的包裹收费 10 元；重量超过1kg 的包裹， 除1kg 收费 10 元之外，每超过1kg （不足1kg ，按1kg 计算）需再收 5 元. 该公司将最近承揽的 100 件包裹的重量统计如下： 包裹重量（单位： kg ） 1 2 3 4 5 包裹件数 43 30 15 8 4 公司对近 60 天，每天揽件数量统计如下表： 包裹件数范围 0~100 101~200 201~300 301~400 401~500 包裹件数（近似处理） 50 150 250 350 450 天数 6 6 30 12 6 以上数据已做近似处理，并将频率视为概率. - 5 - （1）计算该公司未来 5 天内恰有 2 天揽件数在 101~300 之间的概率； （2）①估计该公司对每件包裹收取的快递费的平均值； ②根据以往的经验，公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的 用作其他费用.目前前台有工作人员 3 人，每人每件揽件不超过 150 件，日工资 100 元.公司 正在考虑是否将前台工作人员裁减 1 人，试计算裁员前后公司每日利润的数学期望，若你是 公司老总，是否进行裁减工作人员 1 人？ 20． 已知椭圆   2 2 2: 1 1xC y aa    的离心率为 2 2 ， ,A B 是椭圆C 上的两个不同点. （1）若OA OB ，且点 ,A B 所在的直线方程为  0y x m m   ，求 m 的值； （2）若直线 ,OA OB 的斜率之积为 1 2  ，线段OA 上有一点 M 满足 2 3 OM OA  ，连接 BM 并 延长交椭圆C 于点 M ，试问： BM BN 是否为定值？若是，求出该定值，否则说明理由. 21． 已知函数   lnf x x x ，    2 2 ah x x x a a   R . （1）若直线  0x t t  与曲线  y f x 和  y h x 分别交于 ,A B 两点直线，且曲线  y f x 在 A 处的切线与  y h x 在 B 处的切线相互平行，求正数 a 的最大值； （2）若      21 12 f xg x ax a xx      有三个不同的零点，求 a 的取值范围. 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分． 22．选修 4-4：坐标系与参数方程 在直角坐标系 xOy 中，l 是过定点  4,2P 且倾斜角为 的直线；在极坐标系（以坐标原点O 为极点，以 x 轴非负半轴为极轴，取相同单位长度）中，曲线C 的极坐标方程为 4cos  . （1）写出直线l 的参数方程，并将曲线C 的方程化为直角坐标方程； （2）若曲线C 与直线l 相交于不同的两点 M N、 ，求 PM PN 的取值范围. 23．选修 4-5：不等式选讲 设函数  f x x a  ， 0a  . - 6 - （1）证明：   1 2f x f x       ； （2）若不等式     12 2f x f x  的解集是非空集，求 a 的范围. - 7 - 岳阳市一中 2018 届高三 5 月第一次模拟 数学试题（理科）参考答案(14) 一、选择题 1-5:ACCAB 6-10:DACDB 11、12：CC 二、填空题 13．0 14．3 15．乙、丙、甲 16． 33 2r   三、解答题 17．解：（1）∵ , ,n nn a S 成等差数列，∴ 2 n na n S  又  1 2n n na S S n   ∴  12 n n nS S n S   即 12n nS S n  ∴ 12 2 2 2n nS n S n     ∴  12 2 1 2n nS n S n        又∵ 1 1 2 4 0S     ∴ 2nS n  成等比数列. （2）由（1）知 2nS n  是以 1 13 3 4S a    为首项，2 为公比的等比数列. ∴ 1 12 4 2 2n n nS n       又 2 n na n S  ∴ 12 2 2n na   ∴ 2 1n na    2 1 2n n n nb na n n n       1 2 31 2 2 2 3 2 2n nT n        L  1 2 3 n    L    1 12 1 2 2 n n n nT n       18．解：（1）取 SA 中点 M ，连接 ,BM DM ，可证 SA  面 MBD ， - 8 - 所以异面直线 SA 与 BD 所成的角为 90° （2）设 2BS  ，则 1DM  ， 3BM  ，又 2BD  ，可得 DM BM . 由（1）知 SA DM ，从而 DM  平面 ABC ， 以 M 为坐标原点， , ,MS MB MD 的方向分别为 , ,x y z 轴建立坐标系. 则  1,0,0S ，  1,0,0A  ，  0, 3,0B ，  0,0,1D ，  1, 3,0DC AB  uuur uuur ，所以  1, 3,1C ，  1, 3,0SB   uur ，  1,0,1SD   uur ，  1,0,1BC  uuur ， 可求得平面 SDC 的法向量  3, 1, 3n   r ， 平面 SBC 的法向量  3,1, 3m   ur ， 所以 1cos , 7n m   r ur 又二面角 D SC B  为锐角，故二面角 D SC B  的余弦值为 1 7 . 19．解：（1）样本中包裹件数在 101~300 之间的天数为 36，频率 36 3 60 5f   ， 故可估计概率为 3 5 ， 显然未来 5 天中，包裹件数在 101~300 之间的天数 X 服从二项分布， 即 3~ 5, 5X B     ，故所求概率为 3 2 2 5 2 3 144 5 5 625C            （2）①样本中快递费用及包裹件数如下表： 包裹重量（单位： kg ） 1 2 3 4 5 快递费（单位：元） 10 15 20 25 30 包裹件数 43 30 15 8 4 - 9 - 故样本中每件快递收取的费用的平均值为 10 43 15 30 20 15 25 8 30 4 15100           ， 故该公司对每件快递收取的费用的平均值可估计为 15 元. ②根据题意及（2）①，揽件数每增加 1，公司快递收入增加 15（元）， 若不裁员，则每天可揽件的上限为 450 件，公司每日揽件数情况如下： 故公司平均每日利润的期望值为 1260 15 3 100 10003      （元）； 若裁员 1 人，则每天可揽件的上限为 300 件，公司每日揽件数情况如下： 故公司平均每日利润的期望值为 1235 15 2 100 9753      （元） 因975 1000 ，故公司不应将前台工作人员裁员 1 人. 20．解：（1）由题知 2 1 21 2e a    ，∴ 2 2a  ，∴椭圆 C 的方程为 2 2 12 x y  设  1 1,A x y ，  2 2,B x y ，将直线 y x m  代入椭圆方程，得： 2 23 4 2 2 0x mx m    ∴ 1 2 4 3x x m   ， 2 1 2 2 2 3 mx x  （*） ∵OA OB ，∴ 1 2 1 2 0OA OB x x y y    uur uuur 即   1 2 1 2x x x m x m      2 1 1 1 22 0x x m x x m    - 10 - 将（*）式代入得 23 4m  ，又 0m  ，得 2 3 3m  （2）设 BM BN  ，  1 1,A x y ，  2 2,B x y ，  3 3,N x y 由题知 2 3OM OA uuur uur ，∴ 1 1 2 2,3 3M x y     ， ∴ 1 2 1 2 2 2,3 3BM x x y y      uuur ，  3 2 3 2,BN x x y y   uuur 又∵ BM BN uuur uuur ，∴ 3 1 2 2 1 3x x x     ， 3 1 2 2 1 3y y y     ∵点 N 在椭圆C 上，∴ 2 21 2 1 2 2 1 2 13 12 3 x x y y                 即  22 2 2 21 2 1 22 2 14 9 2 2 x xy y                  1 2 1 22 4 1 13 2 x x y y          （**） ∵ ,A B 点在椭圆C 上，∴ 2 2 2 21 2 1 21, 12 2 x xy y    又直线OA OB、 斜率之积为 1 2  ，∴ 1 2 1 2 1 2 y y x x   ，即 1 2 1 2 02 x x y y  代入（**）得  2 2 2 14 19      ，解得 13 18   故 BM BN 为定值，定值为13 18 . 21．解：（1）依题意，函数  f x 的定义域为 0, ，   ln 1f x x   ，   1h x ax   因 为曲线  y f x 在 A 处的切线与  y h x 在 B 处的切线相互平行， 所以    f x h x  在 0, 有解，即方程 ln 0t at  在 0, 有解. 方程 ln 0t at  在 0, 有解转化为函数 lny x 与函数 y ax 的图象在  0, 上有交 点，令过原点且与函数 lny x 的图象相切的直线的斜率为 k ，只须 0 a k  . - 11 - 令切点为  0 0,lnx x ，则 0 0 1 x xk y x  ，又 0 0 ln xk x  ，所以 0 0 0 ln1 x x x  ，解得 0x e ， 于是 1k e  ，所以 10 a e   ， a 的最大值为 1 e （2）由题意      21 1 ln 02g x x x ax a x      ，则   1 1g x x ax      ， 当 1a  时，∵   1 1 1 0g x x a ax         ， ∴  g x 在  0, 上为增函数，不符合题意. 当 1a  时，    2 1 1x a xg x x     ，令    2 1 1x x a x     ，则     21 4 3 1 0a a a        .令   0x  的两根分别为 1 2,x x 且 1 2x x ， 则∵ 1 2 1 0x x a    ， 1 2 1 0x x   ，∴ 1 20 1x x   ， 当  10,x x 时，   0x  ，∴   0g x  ，∴  g x 在 10, x 上为增函数； 当  1 2,x x x 时，   0x  ，∴   0g x  ，∴  g x 在 1 2,x x 上为减函数； 当  2 ,x x  时，   0x  ，∴   0g x  ，∴  g x 在 2 ,x  上为增函数； ∵  1 0g  ，∴  g x 在 1 2,x x 上只有一个零点 1，且  1 0g x  ，  2 0g x  . ∴ 21 1 2 21 12 a a g e e                              1 1 2 2ln a a e ae a               21 1 1 2 2 21 1 ln2 a a a e e a e                                1 1 2 21 2 02 a a e e                      . ∵ 1 20 1 a e       ，又当  1,1x x 时，   0g x  ，∴ 1 2 10 a e x       ∴  g x 在 10, x 上必有一个零点. ∴      212 2 2 1 ln 2 22g a a a      2 2a a a      21 12 1 2 2 02 2a a a      . ∵ 2 2 1a   ，又当  21,x x 时，   0g x  ，∴ 22 2a x  . ∴  g x 在 2 ,x  上必有一个零点. - 12 - 综上所述，故 a 的取值范围为 1, . 22．解：（1）直线l 的参数方程为 4 cos 2 sin x t y t        （t 为参数）. 曲线 C 的极坐标方程 4cos  可化为 2 4 cos   . 把 cosx   ， siny   代入曲线C 的极坐标方程 可得 2 2 4x y x  ，即  2 22 4x y   . （2）把直线l 的参数方程为 4 cos 2 sin x t y t        （t 为参数）代入圆的方程可得：  2 4 sin cos 4 0t t     ∵曲线C 与直线相交于不同的两点 M N、 ， ∴  216 sin cos 16 0      ， ∴sin cos 0   ，又  0,  ， ∴ 0, 2      . 又  1 2 4 sin cost t      ， 1 2 4t t  . ∴ 1 2 1 2PM PN t t t t      4 sin cos 4 2 sin 4         ， ∵ 0, 2      ，∴ 3,4 4 4              ， ∴ 2sin ,14 2            . ∴ PM PN 的取值范围是4,4 2 . 23．解：（1）函数  f x x a  ， 0a  则   1 1f x f x a ax x            1 1x a a x a ax x        - 13 - 1 1 12 2x x xx x x        （2）    2 2f x f x x a x a     ， 0a  当 x a 时，   2 2 3f x a x a x a x      ，则  f x a  ， 当 2 aa x  时，   2f x x a a x x      ，则  2 a f x a    ， 当 2 ax  时，   2 3 2f x x a x a x a      ，则   2 af x   ， 于是  f x 的值域为 ,2 a    由不等式     12 2f x f x  的解集是非空集，即 1 2 2 a  ， 解得 1a   ，由于 0a  ，则 a 的取值范围是 1,0 .