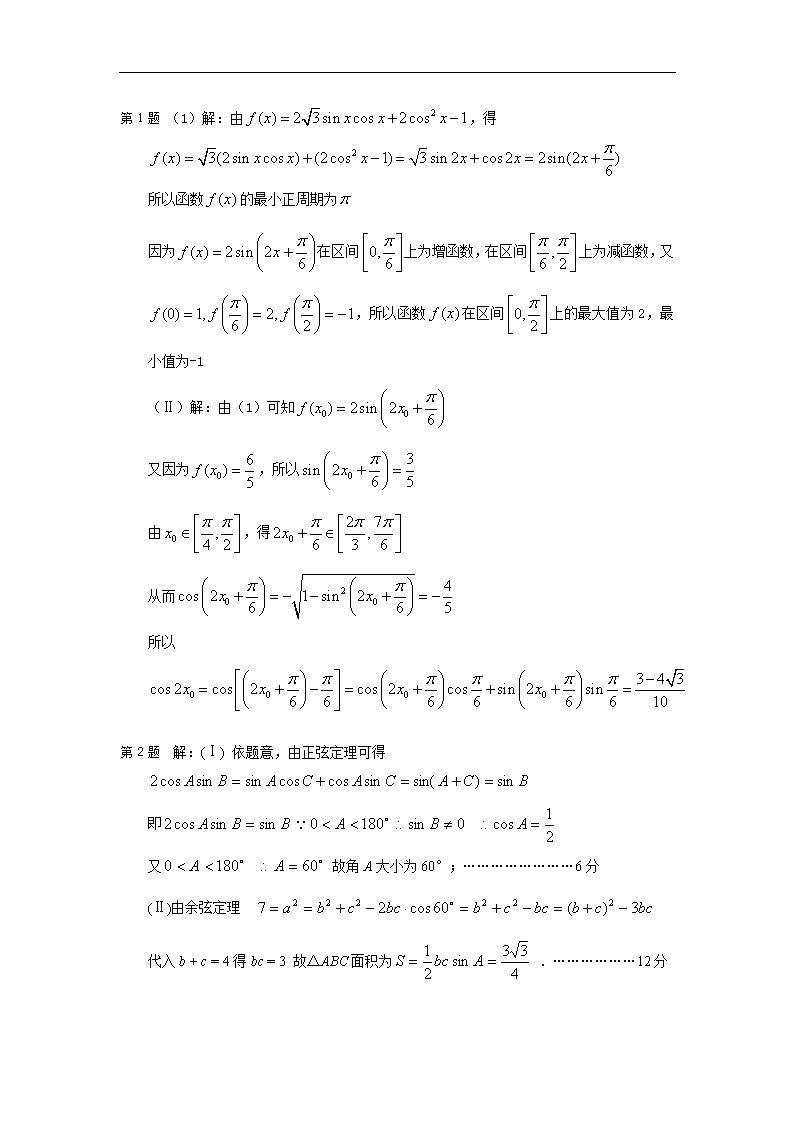高考数学专题复习：三角函数精选精练答案 8页

第1题 （1）解：由，得 所以函数的最小正周期为 因为在区间上为增函数，在区间上为减函数，又 ‎，所以函数在区间上的最大值为2，最小值为-1‎ ‎（Ⅱ）解：由（1）可知 又因为，所以 由，得 从而 所以 第2题 解：(Ⅰ) 依题意，由正弦定理可得 即 ‎ 又 故角A大小为60°；……………………6分 ‎(Ⅱ)由余弦定理 ‎ 代入b + c = 4得bc = 3 故△ABC面积为 ．………………12分 第3题： 本小题主要考查三角函数的定义、两角和与差的三角函数公式、平面向量等基础知识，考查运算求解能力，考查化归与转化思想．满分13分．‎ 解：（Ⅰ）解法一：因为，， ……2分 所以 ………3分 ‎. ………7分 解法二：平移到（移到，移到），………2分 由的坐标与的坐标相等，都等于点的坐标. ………3分 由平几知识易得直线的倾斜角为，‎ ‎∵，∴根据三角函数的定义可得，‎ 所以. ………7分 ‎（Ⅱ）解法一：，………8分 ‎∵，∴， ………9分 ‎∴ ………11分 ‎， ………12分 所以当时，取得最大值. ………13分 解法二：，………8分 ‎∵，∴，即，‎ ‎∴. ………9分 ‎∵，∴， ‎ ‎∴, ………10分 ‎+ Ks5u ‎, ………12分 所以当时，取得最大值. ………13分 第4题 第5题 解：（1） …………2分 对于，‎ ‎ …………3分 又，‎ ‎ ……6分 ‎（2）由B A C B C A sin sin sin ‎2‎ ‎,‎ sin ‎,‎ sin ‎,‎ sin + = 得 成等差数列 ，‎ 由正弦定理得 …………8分 ‎，‎ 即 …………10分 由余弦弦定理， …………11分[来源:学|科|网]‎ ‎，‎ ‎…………13分 第6题：本小题主要考查三角函数的性质、两角和与差的三角函数公式、解三角形以及数列等基础知识，考查运算求解能力，考查函数与方程思想、数形结合思想．满分13分．‎ 解：（Ⅰ）、、成等差，且公差为2，‎ ‎、.……………………………………1分 又，，‎ ‎， …………………………4分 ‎， ‎ 恒等变形得 ，解得或.………………………………5分 又，. ………………………………………6分 ‎（Ⅱ）在中，，………………8分 ‎，‎ ‎，. ‎ 的周长 ‎ ‎，………11分 又，, …………………………12分 当即时，取得最大值． ………13分 第7题 解：（1）在△ABD中，由余弦定理得 BD2＝AB2+AD2－2AB·AD·cosA． ‎ 同理，在△CBD中，BD2＝CB2+CD2－2CB·CD·cosC． ………………… 3分 因为∠A和∠C互补，‎ 所以AB2+AD2－2AB·AD·cosA＝CB2+CD2－2CB·CD·cosC ‎＝CB2+CD2＋2CB·CD·cosA． ………… 5分 即 x2+(9－x)2－2 x(9－x) cosA＝x2+(5－x)2＋2 x(5－x) cosA．　‎ 解得 cosA＝，即f( x)＝．其中x∈(2，5)．　　 ……………………… 8分 ‎（2）四边形ABCD的面积 S＝(AB·AD+ CB·CD)sinA＝[x(5－x)+x(9－x)]．　 ‎ ‎＝x(7－x)＝＝．………… 11分 记g(x)＝(x2－4)( x2－14x＋49)，x∈(2，5)．‎ 由g′(x)＝2x( x2－14x＋49)＋(x2－4)( 2 x－14)＝2(x－7)(2 x2－7 x－4)＝0，‎ 解得x＝4(x＝7和x＝－舍)． ……………………… 14分 所以函数g(x)在区间(2，4)内单调递增，在区间(4，5)内单调递减．‎ 因此g(x)的最大值为g(4)＝12×9＝108．‎ 所以S的最大值为＝6．‎ 答：所求四边形ABCD面积的最大值为6m2． ……………………… 16分 第8题 ‎ 本小题主要考查三角函数的图象与性质、解三角形等基础知识，考查运算求解能力以及应用数学知识分析和解决实际问题的能力，考查化归与转化思想、数形结合思想，‎ 解法一 ‎（Ⅰ）依题意，有，，又，。‎ 当 是，‎ ‎ 又 ‎（Ⅱ）在△MNP中∠MNP=120°，MP=5，‎ 设∠PMN=，则0°<<60°‎ 由正弦定理得 ‎,‎ 故 ‎0°<<60°，当=30°时，折线段赛道MNP最长 亦即，将∠PMN设计为30°时，折线段道MNP最长 解法二：‎ ‎（Ⅰ）同解法一 ‎（Ⅱ）在△MNP中，∠MNP=120°，MP=5，‎ 由余弦定理得∠MNP=‎ 即 故 从而，即 当且仅当时，折线段道MNP最长 注：本题第（Ⅱ）问答案及其呈现方式均不唯一，除了解法一、解法二给出的两种设计方式，还可以设计为：①；②；③点N在线段MP的垂直平分线上等 第9题 解：(I)∵,∴-cosBcosC+sinBsinC-=0,………………………2分 即cosBcosC-sinBsinC=-,∴cos(B+C)=-.…………………………………4分 ‎∵A+B+C=180°,∴cos(B+C)=-cosA,…………………………………………………5分 ‎∴cosA=,A=30°.…………………………………………………………………6分 ‎(Ⅱ)方案一：选择①③可确定△ABC.………………………………………………7分 ‎∵A=30°,a=1,‎2c-(+1)b=0.‎ 由余弦定理,…………………………9分 整理得=2,b=,c=.…………………………………………………11分 ‎∴.………………………13分 方案二：选择①④可确定△ABC.……………………………………………………7分 ‎∵A=30°,a=1,B=45°,∴C=105°.……………………………………………………8分 又sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=.……9分 由正弦定理得c=.……………………………11分 ‎∴.………………………13分 ‎(注：若选择②③,可转化为选择①③解决；若选择②④,可转化为选择①④解决,此略.评分标准可参照以上解法自行制定.选择①②或选择③④不能确定三角形)‎ 第10题 解法一：(Ⅰ)证明:因为，------①‎ ‎，------②……………………………………………2分 ‎①-② 得.------③………………………………3分 ‎9分 所以.……………………………………………10分 ‎ ，……………………………………………8分 因为A,B,C为的内角，所以，‎ ‎12分 所以为直角三角形. ……………………………………………13分 ‎