- 932.50 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第05天 初高中衔接:高次不等式
高考频度:★★☆☆☆ 难易程度:★★★☆☆
典例在线
解关于的不等式:
(1);(2).
【参考答案】(1);(2).
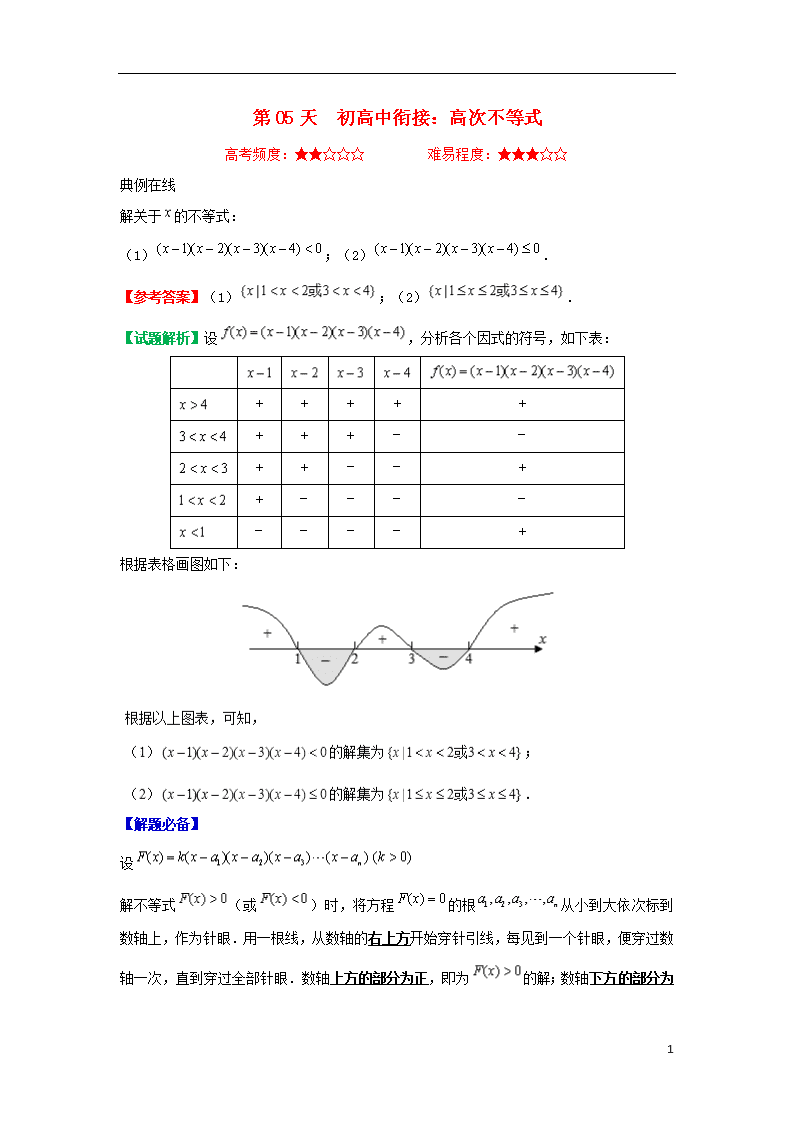
【试题解析】设,分析各个因式的符号,如下表:
+
+
+
+
+
+
+
+
–
–
+
+
–
–
+
+
–
–
–
–
–
–
–
–
+
根据表格画图如下:
【解题必备】
设
解不等式(或)时,将方程的根从小到大依次标到数轴上,作为针眼.用一根线,从数轴的右上方开始穿针引线,每见到一个针眼,便穿过数轴一次,直到穿过全部针眼.数轴上方的部分为正,即为的解;数轴
4
下方的部分为负,即为不等式的解.
注意:
(1)要求的最高次项系数为正;(即每一个的系数为正且,若,则不等式两边同时乘以,并改变不等号的方向)
(2)当根为二重根(即两个相等的实数根)时,按两个针眼对待,即穿过数轴两次(简记为“奇过偶不过”);
(3),;
,(或);
(4),当时,的符号是确定的;
(5)永远从数轴右上方开始;
(6)最后结果数轴上方的部分为不等式的解,数轴下方的部分为不等式的解;
(7)不等式右边须为0,否则先移项,使右边为0;
(8)穿针引线法可以用于解高次不等式,也可以用于解一次、二次不等式,或可以转化为高次不等式的分式不等式等.
学霸推荐
1.解关于的不等式:
(1); (2); (3);
(4); (5).
2.解关于的不等式:
(1); (2).
4
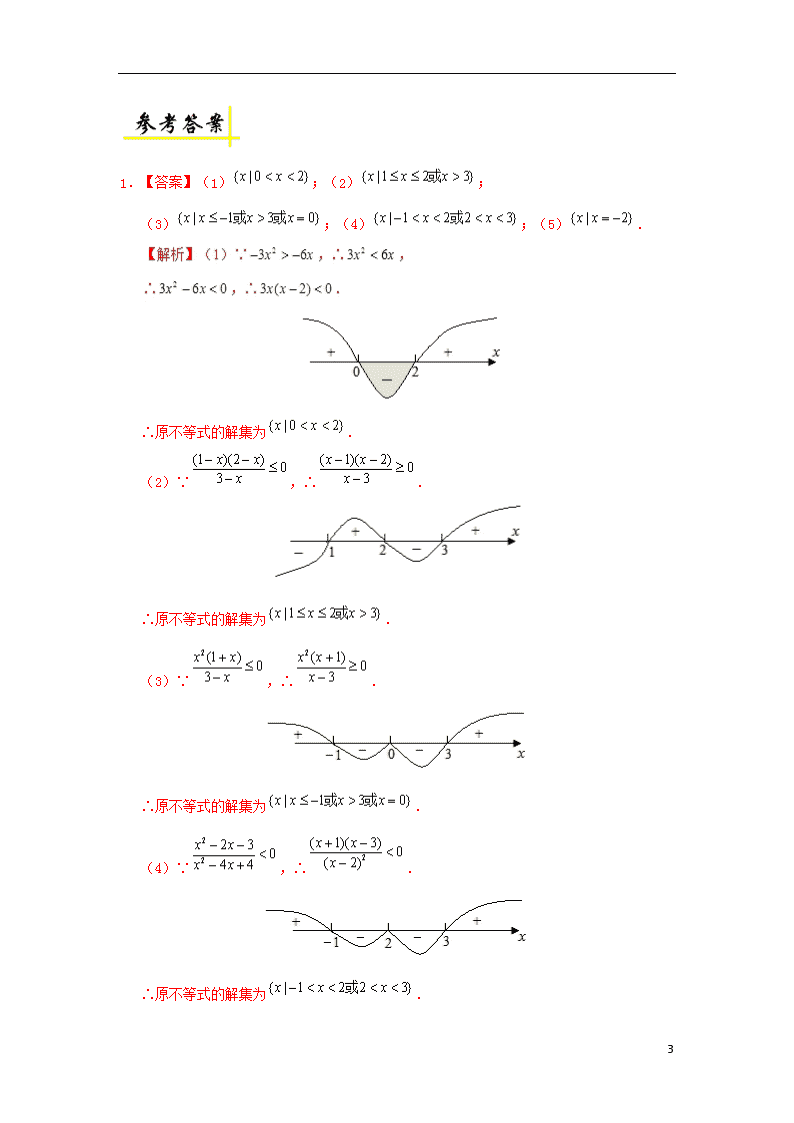
1.【答案】(1);(2);
(3);(4);(5).
∴原不等式的解集为.
(2)∵,∴.
∴原不等式的解集为.
(3)∵,∴.
∴原不等式的解集为.
(4)∵,∴.
∴原不等式的解集为.
4
(5)∵,∴.
∴原不等式的解集为.
2.【答案】(1);(2).
∴原不等式的解集为.
(2)∵,∴,∴,∴.
∴原不等式的解集为.
4
相关文档
- 人教版高中数学选修1-1课件:第二章2021-06-1114页
- 湖北省武汉市部分市级示范高中20192021-06-117页
- 高中数学人教a版必修4模块综合检测2021-06-117页
- 2020_2021学年新教材高中数学第六2021-06-1127页
- 高中数学必修1人教A同步练习试题及2021-06-113页
- 安徽省芜湖市示范高中2020届高三下2021-06-1124页
- 高中数学必修4公开课教案1_4_1 正2021-06-117页
- 高中数学必修1教案1_3_2函数的奇偶2021-06-117页
- 四川省乐山市草堂高中2020-2021学2021-06-114页
- 高中数学人教a版选修2-2(课时训练):1.2021-06-1112页