2020高中数学 第1章 立体几何初步 第三节 空间几何体的表面积和体积习题 苏教版必修2 3页

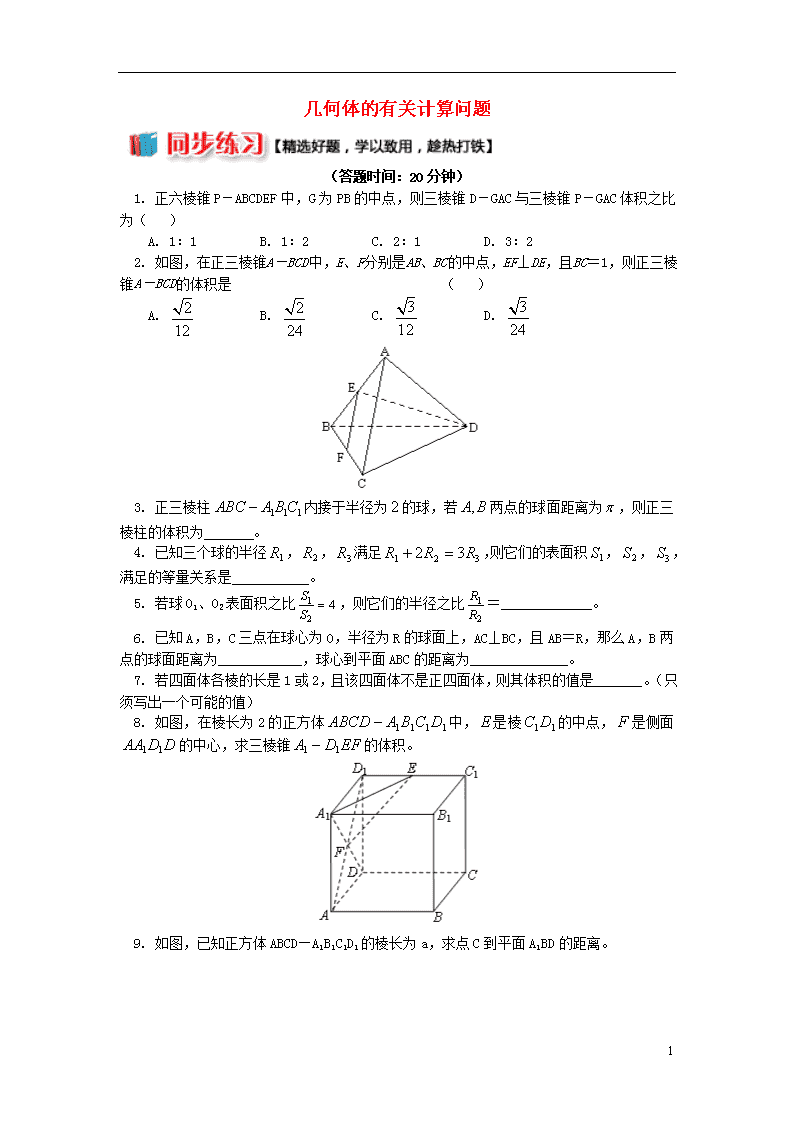
几何体的有关计算问题 ‎（答题时间：20分钟）‎ ‎1. 正六棱锥P－ABCDEF中，G为PB的中点，则三棱锥D－GAC与三棱锥P－GAC体积之比为（ ）‎ A. 1：1 B. 1：‎2 ‎ C. 2：1 D. 3：2 ‎ ‎2. 如图，在正三棱锥A－BCD中，E、F分别是AB、BC的中点，EF⊥DE，且BC＝1，则正三棱锥A－BCD的体积是 （ ）‎ A. B. C. D. ‎ ‎3. 正三棱柱内接于半径为的球，若两点的球面距离为，则正三棱柱的体积为 　　。‎ ‎4. 已知三个球的半径，，满足，则它们的表面积，，，满足的等量关系是___________。‎ ‎5. 若球O1、O2表面积之比，则它们的半径之比＝_____________。‎ ‎6. 已知A，B，C三点在球心为O，半径为R的球面上，AC⊥BC，且AB＝R，那么A，B两点的球面距离为____________，球心到平面ABC的距离为______________。‎ ‎7. 若四面体各棱的长是1或2，且该四面体不是正四面体，则其体积的值是_______。（只须写出一个可能的值）‎ ‎8. 如图，在棱长为2的正方体中，是棱的中点，是侧面的中心，求三棱锥的体积。‎ ‎9. 如图，已知正方体ABCD—A1B‎1C1D1的棱长为a，求点C到平面A1BD的距离。‎ 3‎ 3‎ ‎1. C 2. B 3. 8‎ ‎4. ‎ ‎5. 2‎ ‎6. R R 解析：∵AB＝R，∴△AOB为等边三角形。‎ ‎∴∠AOB＝，∴A，B两点的球面距离为R。‎ 又∵AC⊥BC，所以过A，B，C三点的截面圆的圆心O＇为AB的中点。‎ ‎∴球心到平面ABC的距离OO′＝R。‎ ‎7. 解析：随意画出一四面体即可，如一边长为1而其余边长都为2的四面体，求出底面积后，高可以通过连接相应边的中点和顶点从而和侧棱构成三角形，进而利用等积变换求解。‎ ‎8. 解析：。‎ ‎9. a 解析：点C到平面A1BD的距离就是三棱锥C—A1BD的底面A1BD上的高h的距离.本题我们利用等积变换求解。‎ ‎∵S△ADB＝S△CBD，∴。‎ ‎∴。∴h＝a，点C到平面A1BD的距离为a。‎ 3‎