- 81.50 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
4.1.3 导数的概念和几何意义
一、基础达标
1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线
( )
A.不存在 B.与x轴平行或重合
C.与x轴垂直 D.与x轴斜交
答案 B
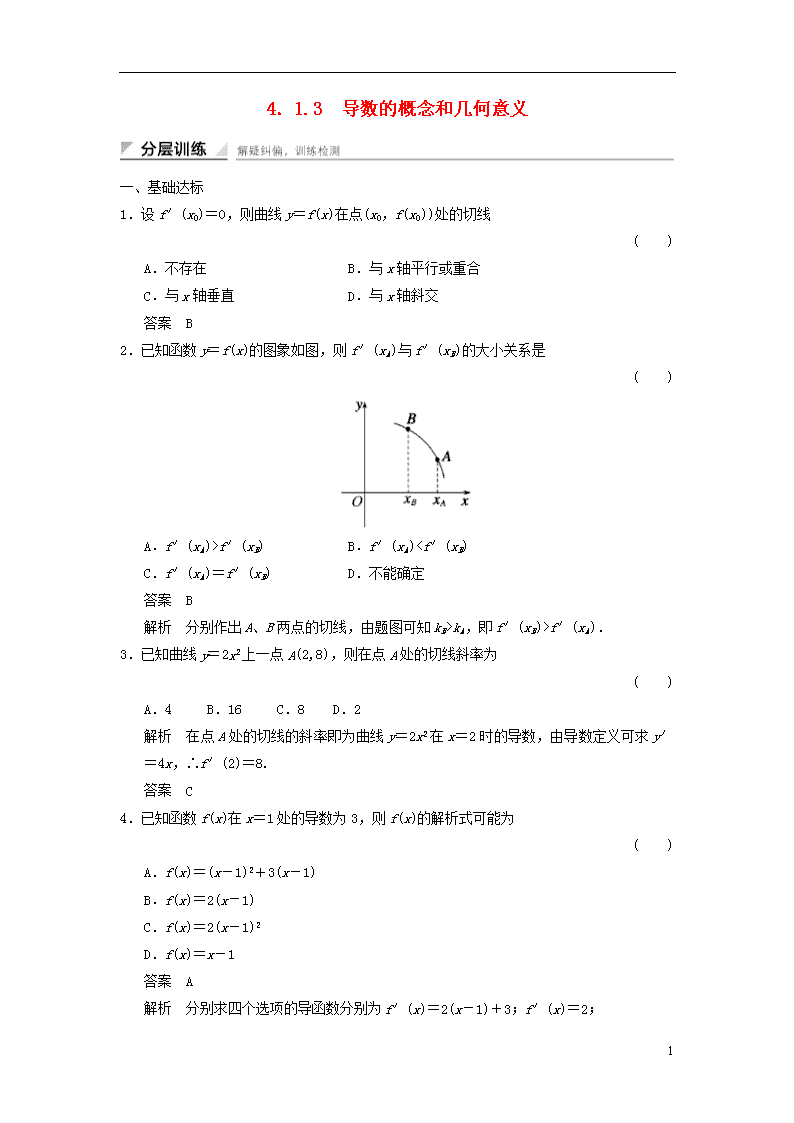
2.已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是
( )
A.f′(xA)>f′(xB) B.f′(xA)kA,即f′(xB)>f′(xA).
3.已知曲线y=2x2上一点A(2,8),则在点A处的切线斜率为
( )
A.4 B.16 C.8 D.2
解析 在点A处的切线的斜率即为曲线y=2x2在x=2时的导数,由导数定义可求y′=4x,∴f′(2)=8.
答案 C
4.已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为
( )
A.f(x)=(x-1)2+3(x-1)
B.f(x)=2(x-1)
C.f(x)=2(x-1)2
D.f(x)=x-1
答案 A
解析 分别求四个选项的导函数分别为f′(x)=2(x-1)+3;f′(x)=2;
4
f′(x)=4(x-1);f′(x)=1.
5.抛物线y=x2+x+2上点(1,4)处的切线的斜率是________,该切线方程为____________.
答案 3 3x-y+1=0
解析 Δy=(1+d)2+(1+d)+2-(12+1+2)=3d+d2,故y′|x=1=
= (3+d)=3.
∴切线的方程为y-4=3(x-1),
即3x-y+1=0.
6.若曲线y=x2-1的一条切线平行于直线y=4x-3,则这条切线方程为____________.
答案 4x-y-5=0
解析 ∵f′(x)==
== (2x+d)=2x.
设切点坐标为(x0,y0),则由题意知f′(x0)=4,即2x0=4,∴x0=2,代入曲线方程得y0=3,故该切线过点(2,3)且斜率为4.所以这条切线方程为
y-3=4(x-2),即4x-y-5=0.
7.求曲线y=x3在点(3,27)处的切线与两坐标轴所围成的三角形的面积.
解 ∵f′(3)=
= = (d2+9d+27)=27,
∴曲线在点(3,27)处的切线方程为y-27=27(x-3),
即27x-y-54=0.
此切线与x轴、y轴的交点分别为(2,0),(0,-54).
∴切线与两坐标轴围成的三角形的面积为S=×2×54=54.
二、能力提升
8.曲线y=-x3+3x2在点(1,2)处的切线方程为
( )
A.y=3x-1 B.y=-3x+5
C.y=3x+5 D.y=2x
答案 A
4
解析
=-Δx2+3.
Δx→0时,-Δx2+3→3.
∴f′(1)=3.即曲线在(1,2)处的切线斜率为3.
所以切线方程为y-2=3(x-1),即y=3x-1.
9.函数y=f(x)图象在M(1,f(1))处的切线方程为y=x+2,则f(1)+f′(1)=________.
答案 3
解析 由已知切点在切线上.
∴f(1)=×1+2=.
切线的斜率f′(1)=.∴f(1)+f′(1)=3.
10.若曲线y=x2+ax+b在点(0,b)处的切线方程为x-y+1=0,则a,b的值分别为________,________.
答案 1 1
解析 ∵点(0,b)在切线x-y+1=0上,
∴-b+1=0,b=1.
又==a+Δx,
∴f′(0)=a=1.
11.已知曲线y=x3+1,求过点P(1,2)的曲线的切线方程.
解 设切点为A(x0,y0),则y0=x+1.
==
Δx2+3x0Δx+3x.
∴f′(x0)=3x,切线的斜率为k=3x.
点(1,2)在切线上,∴2-(x+1)=3x(1-x0).∴x0=1或x0=-.
当x0=1时,切线方程为3x-y-1=0,
当x0=-时,切线方程为3x-4y+5=0.
所以,所求切线方程为3x-y-1=0或3x-4y+5=0.
12.求抛物线y=x2的过点P(,6)的切线方程.
4
解 由已知得,=2x+d,
∴当d→0时,2x+d→2x,
即y′=2x,
设此切线过抛物线上的点(x0,x),
又因为此切线过点(,6)和点(x0,x),
其斜率应满足=2x0,
由此x0应满足x-5x0+6=0.
解得x0=2或3.
即切线过抛物线y=x2上的点(2,4),(3,9).
所以切线方程分别为y-4=4(x-2),y-9=6(x-3).
化简得4x-y-4=0,6x-y-9=0,
此即是所求的切线方程.
三、探究与创新
13.求垂直于直线2x-6y+1=0并且与曲线y=x3+3x2-5相切的直线方程.
解 设切点为P(a,b),函数y=x3+3x2-5的导数为y′=3x2+6x.故切线的斜率
k=y′|x=a=3a2+6a=-3,得a=-1,代入y=x3+3x2-5得,b=-3,即
P(-1,-3).故所求直线方程为y+3=-3(x+1),即3x+y+6=0.
4
相关文档
- 高中数学必修3教案:3_1随机事件的概2021-06-113页
- 2020高中数学 课时分层作业3 任意2021-06-115页
- 高中数学 1_1_3 导数的几何意义同2021-06-116页
- 高中数学选修2-2课时练习第五章 2_2021-06-1110页
- 【新教材】2020-2021学年高中人教A2021-06-1131页
- 高中数学:新人教A版必修二 4_2直线2021-06-116页
- 2019-2020学年高中数学课时作业9柱2021-06-116页
- 2020年高中数学第三章函数的应用章2021-06-118页
- 肇庆市2021届高中毕业班第一次统一2021-06-114页
- 高中数学北师大版新教材必修一课时2021-06-1111页