上海教育高中数学一下对数函数的图像与性质篇 8页

‎4.6对数函数的图像与性质（1）‎ 案例背景 对数函数是函数中又一类重要的基本初等函数，它是在学生已经学过对数与常用对数，反函数以及指数函数的基础上引入的．故是对上述知识的应用，也是对函数这一重要数学思想的进一步认识与理解．对数函数的概念，图象与性质的学习使学生的知识体系更加完整，系统，同时又是对数和函数知识的拓展与延伸．它是解决有关自然科学领域中实际问题的重要工具，是学生今后学习对数方程，对数不等式的基础 案例叙述：‎ ‎(一).创设情境 ‎（师）：前面的几种函数都是以形式定义的方式给出的，今天我们将从反函数的角度介绍新的函数．‎ ‎　　反函数的实质是研究两个函数的关系，所以自然我们应从大家熟悉的函数出发，再研究其反函数．这个熟悉的函数就是指数函数．‎ ‎　　（提问）：什么是指数函数?指数函数存在反函数吗?‎ ‎（学生）： 是指数函数，它是存在反函数的 ‎（师）：求反函数的步骤 ‎（由一个学生口答求反函数的过程）：‎ 由 得 ．又 的值域为 ，‎ ‎　　 所求反函数为 ．‎ ‎　　（师）：那么我们今天就是研究指数函数的反函数-----对数函数．‎ ‎（二）新课 ‎　　1.（板书） 定义：函数 的反函数 叫做对数函数．‎ ‎　　（师）：由于定义就是从反函数角度给出的，所以下面我们的研究就从这个角度出发．如从定义中你能了解对数函数的什么性质吗?最初步的认识是什么?‎ ‎　　（教师提示学生从反函数的三定与三反去认识，学生自主探究，合作交流） ‎ ‎（学生）对数函数的定义域为 ，对数函数的值域为 ，且底数 就是指数函数中的 ，故有着相同的限制条件 ．‎ ‎　　（在此基础上，我们将一起来研究对数函数的图像与性质．）‎ ‎2．研究对数函数的图像与性质 ‎ ‎（提问）用什么方法来画函数图像?‎ ‎（学生1）利用互为反函数的两个函数图像之间的关系，利用图像变换法画图．‎ ‎（学生2）用列表描点法也是可以的。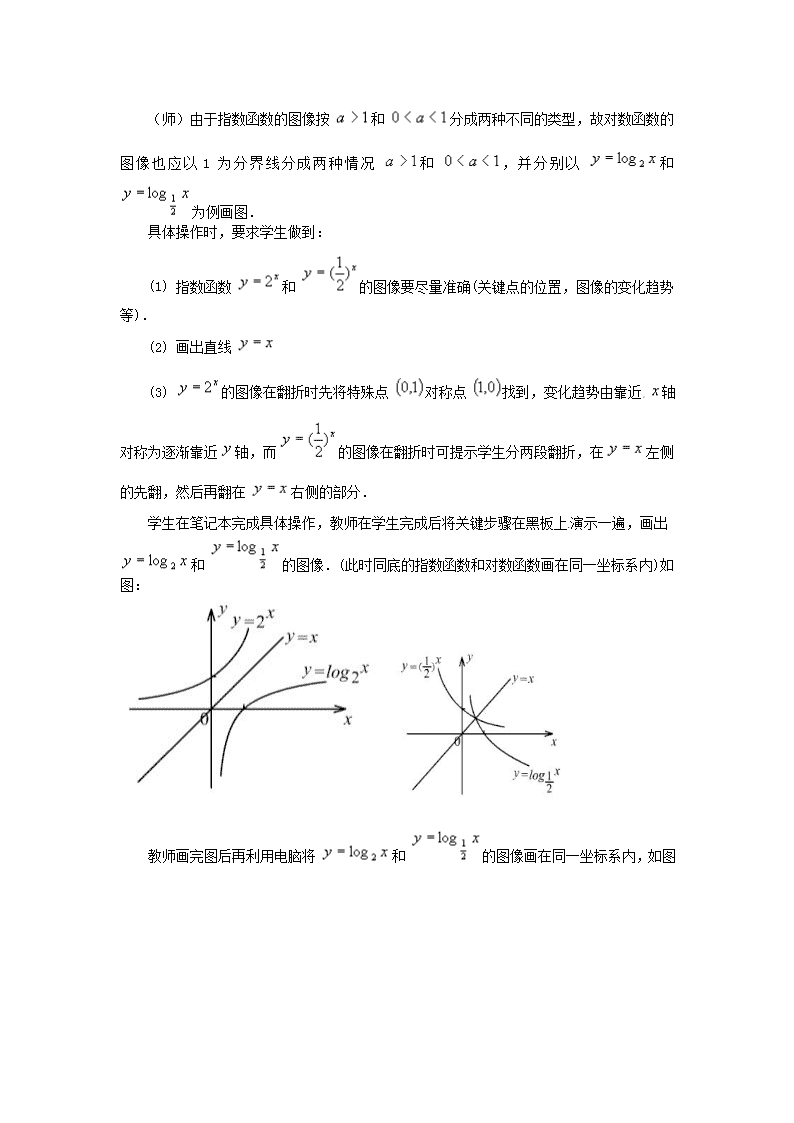‎ 请学生从中上述方法中选出一种，大家最终确定用图像变换法画图．‎ ‎　　（师）由于指数函数的图像按 和 分成两种不同的类型，故对数函数的图像也应以1为分界线分成两种情况 和 ，并分别以 和 为例画图．‎ ‎　　具体操作时，要求学生做到：‎ ‎　　(1) 指数函数 和 的图像要尽量准确(关键点的位置，图像的变化趋势等)．‎ ‎　　(2) 画出直线 ‎ ‎　　(3) 的图像在翻折时先将特殊点 对称点 找到，变化趋势由靠近 轴对称为逐渐靠近 轴，而 的图像在翻折时可提示学生分两段翻折，在 左侧的先翻，然后再翻在 右侧的部分．‎ ‎　　学生在笔记本完成具体操作，教师在学生完成后将关键步骤在黑板上演示一遍，画出 和 的图像．(此时同底的指数函数和对数函数画在同一坐标系内)如图：‎ ‎  ‎ ‎　　教师画完图后再利用电脑将 和 的图像画在同一坐标系内，如图 ‎　　然后提出让学生根据图像说出对数函数的性质(要求从几何与代数两个角度说明)[‎ ‎3. 性质 ‎　　(1) 定义域： ‎ ‎　　(2) 值域： ‎ ‎　　由以上两条可说明图像位于 轴的右侧．‎ ‎(3)图像恒过(1,0)‎ ‎(4) 奇偶性：既不是奇函数也不是偶函数，即它不关于原点对称，也不关于 轴对称 ‎　　(5) 单调性：与 有关．当 时，在 上是增函数．即图像是上升的 ‎                 当 时，在 上是减函数，即图像是下降的．‎ ‎　　之后可以追问学生有没有最大值和最小值，当得到否定答案时，可以再问能否看待何时函数值为正?学生看着图可以答出应有两种情况：‎ ‎　　当 时，有 ；当 时，有 ．‎ ‎　　学生回答后教师可指导学生巧记这个结论的方法：当底数与真数在1的同侧时函数值为正，当底数与真数在1的两侧时，函数值为负，并把它当作第(6)条性质板书记下来]‎ ‎　　最后教师在总结时，强调记住性质的关键在于要脑中有图．且应将其性质与指数函数的性质对比记忆．(特别强调它们单调性的一致性)‎ ‎　　对图像和性质有了一定的了解后，一起来看看它们的应用．‎ ‎（三）．简单应用  ‎ ‎1. 研究相关函数的性质 例1.  求下列函数的定义域：‎ ‎　　(1)      (2)    (3) ‎ 先由学生依次列出相应的不等式，其中特别要注意对数中真数和底数的条件限制．‎ ‎2. 利用单调性比较大小 例2.  比较下列各组数的大小 ‎　　(1) 与 ；      (2) 与 ；   ‎ ‎　　(3) 与 ；           (4) 与 ．‎ ‎　　让学生先说出各组数的特征即它们的底数相同，故可以构造对数函数利用单调性来比大小．最后让学生以其中一组为例写出详细的比较过程．‎ 三．拓展练习 练习：若 ，求 的取值范围．‎ 四．小结及作业 案例反思：‎ 本节的教学重点是理解对数函数的定义，掌握对数函数的图象性质．难点是利用指数函数的图象和性质得到对数函数的图象和性质．由于对数函数的概念是一个抽象的形式，学生不易理解，而且又是建立在指数与对数关系和反函数概念的基础上，通过互为反函数的两个函数的关系由已知函数研究未知函数的性质，这种方法是第一次使用，学生不适应，把握不住关键，因而在教学上采取教师逐步引导，学生自主合作的方式，从学生熟悉的指数问题出发，通过对指数函数的认识逐步转化为对对数函数的认识，而且画对数函数图象时，既要考虑到对底数的分类讨论而且对每一类问题也可以多选几个不同的底，画在同一个坐标系内，便于观察图象的特征，找出共性，归纳性质． 　　在教学中一定要让学生动手做，动脑想，大胆猜，要以学生的研究为主，教师只是不断地以反函数这条主线引导学生思考的方向．这样既增强了学生的参与意识又教给他们思考问题的方法，获取知识的途径，使学生学有所思，思有所得，练有所获，，从而提高学习兴趣．‎ 课题：对数函数的图像与性质（2）（教案）‎ ‎【教学目标】‎ 知识与技能目标：（1）进一步熟悉对数函数的图像和性质（2）会利用对数函数的性质解决数学问题；（3）培养学生数形结合的意识。‎ 过程与方法目标：体会分类讨论、数形结合、转换与化归等数学思想，从变式教学的过程中体验数学知识点之间的内在联系，学会观察与归纳。‎ 情感、态度与价值观目标：体验数学活动的过程，让学生获得发现的成就感，在质疑、交流、合作中形成良好的数学思维品质。‎ ‎　　【教学重点】对数函数性质的应用，主要是对数函数单调性的应用。‎ ‎【教学难点】与对数函数相关的函数值域问题。‎ ‎【教学方法】主要采用“变式教学”和“引导探究法”开展教学活动。‎ ‎【教学过程】‎ 一、 复习对数函数的图像与性质 二、对数函数性质的应用 例1、已知函数，，试比较f(x)与g(x)的大小K]‎ 例2、求下列各式中实数a的取值范围：‎ ‎（1）； （2）>3； （3）<1。‎ 练习：>1‎ 例3、求函数的值域。‎ 变式1： ‎ 变式2： [‎ 变式3： ‎ 变式4： [ K]‎ 变式5： 若函数的值域为R，求实数a的取值范围。‎ 变式6： 若函数的定义域为R呢？‎ 课后思考：若函数的定义域为R，求实数a的取值范围；值域为R呢？‎ 练习：求函数，其中的值域。‎ 三、课堂小结 四、作业布置[来 w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com ‎4.6对数函数的图像与性质 ‎【教学目标】：‎ 知识与技能：理解对数函数的概念，掌握它们的基本性质，进一步领会研究函数的基本方法 过程与方法： 复习与实例引入、利用互为反函数的关系研究图像与性质 情感态度与价值观：体会对数函数的应用价值，体验数学建模、求解和解释的过程 ‎【教学重点与难点】]‎ 重点： 对数函数的概念；对数函数的性质；研究函数的方法 难点：对数函数的性质 ‎【教学过程】：‎ 一． 复习：反函数的概念；通过实例和反函数的概念导出对数函数的概念 通过关于细胞分裂的具体实例，直接了解对数函数模型所刻画的数量关系，使学生科学的发展源于实际生活，感受到指数函数与对数函数的密切关系：它们是从不同角度、不同需求看待同一个客观事实，前者根据细胞分裂次数，获得分裂后的细胞数；后者根据分裂后的细胞数，获得分裂的次数.前者用指数函数表示，后者用对数函数.‎ ‎（1）引入：在我们学习研究指数函数时，曾经讨论过细胞分裂问题.某种细胞分裂时，得到的细胞的个数是分裂次数的函数，这个函数可用指数函数表示.‎ 现在来研究相反的问题，如果要求这种细胞经过多少次分裂，可以得到1万个、10万个、……细胞，那么分裂次数就是要得到的细胞个数的函数.根据对数的定义，这个函数可以写成对数的形式，就是.‎ 如果用表示自变量，表示函数，这个函数就是 由反函数的概念，可知函数与指数函数互为反函数.‎ ‎（2）定义：一般地，函数（且）就是指数函数（且）的反函数.因为的值域是，所以，函数的定义域是 二． 通过对数函数和指数函数的关系利用互为反函数的两函数的关系探求对数函数的图像和性质 提问绘制图像的方法：（1）利用反函数的关系；（2）描点绘图 图像 [‎ ‎ ‎ ‎ Ｙ ‎ ‎ ‎ Ｏ Ｘ[]‎ 性质 对数函数 []‎ 性质1.对数函数的图像都在Ｙ轴的右方.‎ 性质2.对数函数的图像都经过点（1，0）‎ 性质3.当时，； 当时，；‎ ‎ 当时，. 当时，.‎ 性质4.对数函数在上是增函数. 对数函数在上是减函数.‎ 一． 掌握对数函数的图像和性质———巩固与应用对数函数的性质解决简单问题 例1. 求下列函数的定义域 ‎；（2）；（3）]‎ 解（1）因为，即，所以函数的定义域是.‎ ‎（2）因为，即，所以函数的定义域是.‎ ‎（3）因为，即，所以函数的定义域是.‎ 例2.利用对数函数的性质，比较下列各题中两个值的大小：‎ ‎（1）和; (2) 和； （3）和，其中 解（1）因为对数函数在上是增函数，又，所以<.‎ ‎ （2）因为对数函数在上是减函数，又3<,所以>.‎ ‎ (3)①当时，因为对数函数在上是增函数，又，所以>.‎ ‎②当时，因为对数函数在上是减函数，又，所以<.K]‎ 例3.“学习曲线”可以用来描述学习某一任务的速度，假设函数中，表示达到某一英文打字水平（字/ 分）所需的学习时间（时），表示每分钟打出的字数（字/ 分）.‎ （1） 计算要达到20字/ 分、40字/ 分所需的学习时间；（精确到“时”）‎ （2） 利用（1）的结果，结合对数性质的分析，作出函数的大致图像 解（1）用计算器计算，得＝20时，＝16；＝40时，＝37.‎ 所以，要达到这两个水平分别需要时间16小时和37小时 ‎(2)由>0，得<90.当增大时， 随得增大而减小.‎ 又为递增函数，随得增大而减小.‎ 从而有随得增大而增大，所以为递增函数. ‎ 由（1）知函数图像过点（20，16）、（40，37）.]‎ 另外，当=0时＝0，所以函数图像过点（0，0）. Ｏ 根据上述这些点得坐标描点作图 ‎ ‎ N 四.练习：教科书P20页‎1.2.3‎.4.5.6‎ 作业：练习册P5页1————4；《一课一练》‎ 五.小结：对数函数的概念、图像、性质 教学反思：‎ ‎ ‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com