高考数学专题复习课件：8-4直线、平面平行的判定与性质 58页

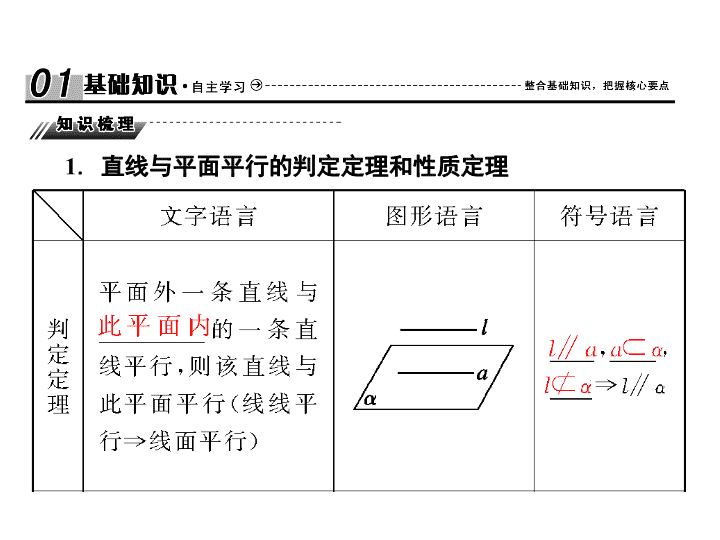
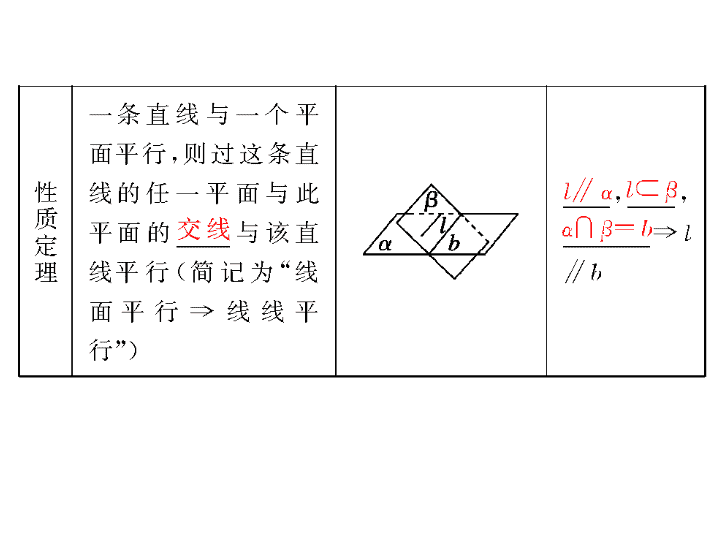
§8.4 　直线、平面平行的判定与性质 ［ 考纲要求］ 1. 能以立体几何中的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理 .2. 能运用公理、定理和已获得的结论证明一些空间图形的平行关系的简单命题 . 1 ． 直线与平面平行的判定定理和性质定理 2. 平面与平面平行的判定定理和性质定理 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面． ( 　　 ) (2) 若一条直线平行于一个平面，则这条直线平行于这个平面内的任一条直线． ( 　　 ) (3) 如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行． ( 　　 ) (4) 如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面． ( 　　 ) (5) 若直线 a 与平面 α 内无数条直线平行，则 a ∥ α .( 　　 ) (6) 空间四边形 ABCD 中， E ， F 分别是 AB ， AD 的中点，则 EF ∥ 平面 BCD .( 　　 ) (7) 若 α ∥ β ，直线 a ∥ α ，则 a ∥ β .( 　　 ) 【 答案 】 (1) × 　 (2) × 　 (3) × 　 (4) √ 　 (5) × 　 (6) √ 　 (7) × 1 ．一条直线 l 上有相异三个点 A 、 B 、 C 到平面 α 的距离相等，那么直线 l 与平面 α 的位置关系是 ( 　　 ) A ． l ∥ α 　　　　　　　　　 B ． l ⊥ α C ． l 与 α 相交但不垂直 D ． l ∥ α 或 l ⊂ α 【 解析 】 当距离不为零时， l ∥ α ，当距离为零时， l ⊂ α . 【 答案 】 D 2 ．设 α ， β ， γ 为三个不同的平面， m ， n 是两条不同的直线，在命题 “ α ∩ β ＝ m ， n ⊂ γ ，且 ________ ，则 m ∥ n ” 中的横线处填入下列三组条件中的一组，使该命题为真命题． ① α ∥ γ ， n ⊂ β ； ② m ∥ γ ， n ∥ β ； ③ n ∥ β ， m ⊂ γ . 可以填入的条件有 ( 　　 ) A ． ① 或 ② B ． ② 或 ③ C ． ① 或 ③ D ． ① 或 ② 或 ③ 【 解析 】 由面面平行的性质定理可知， ① 正确；当 n ∥ β ， m ⊂ γ 时， n 和 m 在同一平面内，且没有公共点，所以平行， ③ 正确．故选 C. 【 答案 】 C 3 ． ( 教材改编 ) 下列命题中正确的是 ( 　　 ) A ．若 a ， b 是两条直线，且 a ∥ b ，那么 a 平行于经过 b 的任何平面 B ．若直线 a 和平面 α 满足 a ∥ α ，那么 a 与 α 内的任何直线平行 C ．平行于同一条直线的两个平面平行 D ．若直线 a ， b 和平面 α 满足 a ∥ b ， a ∥ α ， b ⊄ α ，则 b ∥ α 【 解析 】 A 中， a 可以在过 b 的平面内； B 中， a 与 α 内的直线可能异面； C 中，两平面可相交； D 中，由直线与平面平行的判定定理知， b ∥ α ，正确． 【 答案 】 D 4 ． (2017· 乌鲁木齐二诊 ) 已知直线 l ， m ，其中只有 m 在平面 α 内，则 “ l ∥ α ” 是 “ l ∥ m ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 【 解析 】 若 l ∥ α ，则 l 与 α 内的直线平行或异面；若 l ∥ m ， l 不在平面 α 内，则 l ∥ α ，所以 “ l ∥ α ” 是 “ l ∥ m ” 的必要不充分条件． 【 答案 】 B 5 ．过三棱柱 ABC A 1 B 1 C 1 任意两条棱的中点作直线，其中与平面 ABB 1 A 1 平行的直线共有 ________ 条． 【 解析 】 各中点连线如图，只有面 EFGH 与面 ABB 1 A 1 平行，在四边形 EFGH 中有 6 条符合题意． 【 答案 】 6 题型一　直线与平面平行的判定与性质 命题点 1 　直线与平面平行的判定 【 例 1 】 (2017· 南通模拟 ) 如图所示，斜三棱柱 ABC A 1 B 1 C 1 中，点 D ， D 1 分别为 AC ， A 1 C 1 上的中点． (1) 证明： AD 1 ∥ 平面 BDC 1 . (2) 证明： BD ∥ 平面 AB 1 D 1 . (2) 连接 D 1 D ， ∵ BB 1 ∥ 平面 ACC 1 A 1 ， BB 1 ⊂ 平面 BB 1 D 1 D ， 平面 ACC 1 A 1 ∩ 平面 BB 1 D 1 D ＝ D 1 D ， ∴ BB 1 ∥ D 1 D ， 又 D 1 ， D 分别为 A 1 C 1 与 AC 的中点， ∴ BB 1 ＝ DD 1 ， 故四边形 BDD 1 B 1 为平行四边形， ∴ BD ∥ B 1 D 1 ， 又 BD ⊄ 平面 AB 1 D 1 ， B 1 D 1 ⊂ 平面 AB 1 D 1 ， ∴ BD ∥ 平面 AB 1 D 1 . (1) 证明： GH ∥ EF ； (2) 若 EB ＝ 2 ，求四边形 GEFH 的面积． 【 解析 】 (1) 证明 因为 BC ∥ 平面 GEFH ， BC ⊂ 平面 PBC ， 且平面 PBC ∩ 平面 GEFH ＝ GH ， 所以 GH ∥ BC . 同理可证 EF ∥ BC ，因此 GH ∥ EF . (2) 如图，连接 AC ， BD 交于点 O ， BD 交 EF 于点 K ，连接 OP ， GK . 因为 PA ＝ PC ， O 是 AC 的中点，所以 PO ⊥ AC ， 同理可得 PO ⊥ BD . 又 BD ∩ AC ＝ O ，且 AC ， BD 都在底面内， 所以 PO ⊥ 底面 ABCD . 又因为平面 GEFH ⊥ 平面 ABCD ， 且 PO ⊄ 平面 GEFH ，所以 PO ∥ 平面 GEFH . 因为平面 PBD ∩ 平面 GEFH ＝ GK ， 所以 PO ∥ GK ，且 GK ⊥ 底面 ABCD ，从而 GK ⊥ EF . 所以 GK 是梯形 GEFH 的高． 【 方法规律 】 判断或证明线面平行的常用方法： (1) 利用线面平行的定义 ( 无公共点 ) ； (2) 利用线面平行的判定定理 ( a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α ) ； (3) 利用面面平行的性质定理 ( α ∥ β ， a ⊂ α ⇒ a ∥ β ) ； (4) 利用面面平行的性质 ( α ∥ β ， a ⊄ β ， a ∥ α ⇒ a ∥ β ) ． 跟踪训练 1 (1) 如图所示，在四棱锥 P ABCD 中， ∠ ABC ＝ ∠ ACD ＝ 90 ° ， ∠ BAC ＝ ∠ CAD ＝ 60 ° ， E 为 PD 的中点， AB ＝ 1 ，求证： CE ∥ 平面 PAB ； (2) 如图所示， CD ， AB 均与平面 EFGH 平行， E ， F ， G ， H 分别在 BD ， BC ， AC ， AD 上，且 CD ⊥ AB . 求证：四边形 EFGH 是矩形． 【 证明 】 (1) 由已知条件有 AC ＝ 2 AB ＝ 2 ， AD ＝ 2 AC ＝ 4 ， CD ＝ 2. 如图所示，延长 DC ， AB ，设其交于点 N ，连接 PN ， 因为 ∠ NAC ＝ ∠ DAC ＝ 60 ° ， AC ⊥ CD ， 所以 C 为 ND 的中点， 又因为 E 为 PD 的中点，所以 EC ∥ PN ， 因为 EC ⊄ 平面 PAB ， PN ⊂ 平面 PAB ， 所以 CE ∥ 平面 PAB . (2) ∵ CD ∥ 平面 EFGH ， 而平面 EFGH ∩ 平面 BCD ＝ EF ， ∴ CD ∥ EF . 同理 HG ∥ CD ，且 HE ∥ AB ， ∴ EF ∥ HG . 同理 HE ∥ GF ， ∴ 四边形 EFGH 为平行四边形． ∴ CD ∥ EF ， HE ∥ AB ， ∴∠ HEF 为异面直线 CD 和 AB 所成的角． 又 ∵ CD ⊥ AB ， ∴ HE ⊥ EF . ∴ 平行四边形 EFGH 为矩形． 题型二　平面与平面平行的判定与性质 【 例 3 】 如图所示，在三棱柱 ABC A 1 B 1 C 1 中， E ， F ， G ， H 分别是 AB ， AC ， A 1 B 1 ， A 1 C 1 的中点，求证： (1) B ， C ， H ， G 四点共面； (2) 平面 EFA 1 ∥ 平面 BCHG . 【 证明 】 (1) ∵ G ， H 分别是 A 1 B 1 ， A 1 C 1 的中点， ∴ GH 是 △ A 1 B 1 C 1 的中位线， ∴ GH ∥ B 1 C 1 . 又 ∵ B 1 C 1 ∥ BC ， ∴ GH ∥ BC ， ∴ B ， C ， H ， G 四点共面． (2) ∵ E ， F 分别是 AB ， AC 的中点， ∴ EF ∥ BC . ∵ EF ⊄ 平面 BCHG ， BC ⊂ 平面 BCHG ， ∴ EF ∥ 平面 BCHG . 【 引申探究 】 1 ．在本例条件下，若 D 为 BC 1 的中点，求证： HD ∥ 平面 A 1 B 1 BA . 【 证明 】 如图所示，连接 HD ， A 1 B ， ∵ D 为 BC 1 的中点， H 为 A 1 C 1 的中点， ∴ HD ∥ A 1 B ， 又 HD ⊄ 平面 A 1 B 1 BA ， A 1 B ⊂ 平面 A 1 B 1 BA ， ∴ HD ∥ 平面 A 1 B 1 BA . 2 ．在本例条件下，若 D 1 ， D 分别为 B 1 C 1 ， BC 的中点，求证：平面 A 1 BD 1 ∥ 平面 AC 1 D . 【 证明 】 如图所示，连接 A 1 C 交 AC 1 于点 M ， ∵ 四边形 A 1 ACC 1 是平行四边形， ∴ M 是 A 1 C 的中点，连接 MD ， ∵ D 为 BC 的中点， ∴ A 1 B ∥ DM . ∴ DC 1 ∥ BD 1 . 又 DC 1 ⊄ 平面 A 1 BD 1 ， BD 1 ⊂ 平面 A 1 BD 1 ， ∴ DC 1 ∥ 平面 A 1 BD 1 ， 又 ∵ DC 1 ∩ DM ＝ D ， DC 1 ， DM ⊂ 平面 AC 1 D ， ∴ 平面 A 1 BD 1 ∥ 平面 AC 1 D . 【 方法规律 】 证明面面平行的方法： (1) 面面平行的定义； (2) 面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行； (3) 利用垂直于同一条直线的两个平面平行； (4) 两个平面同时平行于第三个平面，那么这两个平面平行； (5) 利用 “ 线线平行 ” 、 “ 线面平行 ” 、 “ 面面平行 ” 的相互转化 . 跟踪训练 2 如图，在正方体 ABCD A 1 B 1 C 1 D 1 中， S 是 B 1 D 1 的中点， E ， F ， G 分别是 BC 、 DC 、 SC 的中点，求证： (1) 直线 EG ∥ 平面 BDD 1 B 1 ； (2) 平面 EFG ∥ 平面 BDD 1 B 1 . 【 证明 】 (1) 如图，连接 SB ， ∵ E ， G 分别是 BC 、 SC 的中点， ∴ EG ∥ SB . 又 ∵ SB ⊂ 平面 BDD 1 B 1 ， EG ⊄ 平面 BDD 1 B 1 ， ∴ 直线 EG ∥ 平面 BDD 1 B 1 . (2) 连接 SD ， ∵ F 、 G 分别是 DC 、 SC 的中点， ∴ FG ∥ SD . 又 ∵ SD ⊂ 平面 BDD 1 B 1 ， FG ⊄ 平面 BDD 1 B 1 ， ∴ FG ∥ 平面 BDD 1 B 1 ， 又 EG ⊂ 平面 EFG ， FG ⊂ 平面 EFG ， EG ∩ FG ＝ G ， ∴ 平面 EFG ∥ 平面 BDD 1 B 1 . 题型三　平行关系的综合应用 【 例 4 】 如图所示，在四面体 ABCD 中，截面 EFGH 平行于对棱 AB 和 CD ，试问截面在什么位置时其截面面积最大？ 【 解析 】 ∵ AB ∥ 平面 EFGH ， 平面 EFGH 与平面 ABC 和平面 ABD 分别交于 FG 、 EH . ∴ AB ∥ FG ， AB ∥ EH ， ∴ FG ∥ EH ，同理可证 EF ∥ GH ， ∴ 截面 EFGH 是平行四边形． 设 AB ＝ a ， CD ＝ b ， ∠ FGH ＝ α ( α 即为异面直线 AB 和 CD 所成的角或其补角 ) ． 【 方法规律 】 利用线面平行的性质，可以实现与线线平行的转化，尤其在截面图的画法中，常用来确定交线的位置，对于最值问题，常用函数思想来解决． 【 解析 】 如图所示，在平面 PCD 内，过 E 作 EG ∥ CD 交 PD 于 G ， 连接 AG ，在 AB 上取点 F ，使 AF ＝ EG ， ∵ EG ∥ CD ∥ AF ， EG ＝ AF ， ∴ 四边形 FEGA 为平行四边形， ∴ FE ∥ AG . 又 AG ⊂ 平面 PAD ， FE ⊄ 平面 PAD ， ∴ EF ∥ 平面 PAD . ∴ F 即为所求的点． (2) 当点 E 位于棱 SD 上靠近 D 的三等分点处时，可使 CE ∥ 平面 SAB .(8 分 ) 【 答题模板 】 解决立体几何中的探索性问题的步骤 第一步：写出探求的最后结论． 第二步：证明探求结论的正确性． 第三步：给出明确答案． 第四步：反思回顾，查看关键点、易错点和答题规范． 【 温馨提醒 】 (1) 立体几何中的探索性问题主要是对平行、垂直关系的探究，对条件和结论不完备的开放性问题的探究，解决这类问题一般根据探索性问题的设问，假设其存在并探索出结论，然后在这个假设下进行推理论证，若得到合乎情理的结论就肯定假设，若得到矛盾的结论就否定假设． (2) 这类问题也可以按类似于分析法的格式书写步骤：从结论出发 “ 要使 …… 成立 ” ， “ 只需使 …… 成立 ” . (3) 推论； (4) a ⊥ α ， a ⊥ β ⇒ α ∥ β . ► 失误与防范 1 ．在推证线面平行时，一定要强调直线不在平面内，否则会出现错误． 2 ．在解决线面、面面平行的判定时，一般遵循从 “ 低维 ” 到 “ 高维 ” 的转化，即从 “ 线线平行 ” 到 “ 线面平行 ” ，再到 “ 面面平行 ” ；而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于 “ 模式化 ” ． 3 ．解题中注意符号语言的规范应用 .