全国大联考 2020 届 12 月联考理科数学A试卷 8页

理科数学试卷 第 1 页（共 8 页） 20·LK·YG12 绝密★考试结束前 [考试时间：2019 年 12 月 5 日 15:00~17:00] 全国大联考 2020 届 12 月联考 理科数学试卷（A） 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，需用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改 动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。 3．考试结束后，请将试卷和答题卡一并交回。 4．考试时间 120 分钟，满分 150 分 一、选择题：共 12 小题，每小题 5 分，共 60 分．在每个小题给出的四个选项中，只有 一项是符合题目要求的． 1．已知集合 1{ | 2 4}4 xAx=   ， { | 2 2 }B y y x x= = − + − ，则 AB=I A．{2} B．{0} C．[ 2,2]− D．[0,2] 2．若复数 z 满足( 1) 4 2z i i− = + ，则 z = A． 25 B． 17 C． 5 D．17 3．从 [ 6,9]− 中任取一个 m ，则直线3 4 0x y m+ + = 被圆 222xy+=截得的弦长大于 2 的概率为 A． 2 3 B． 2 5 C． 1 3 D． 1 5 4．《张丘建算经》是早于《九章算术》的我国另一部数学著作，在《算经》中有一题： 某女子善于织布，一天比一天织的快，而且每天增加的数量相同，已知第一天织布 5 尺， 30 天共织布 390 尺，则该女子织布每天增加 A． 4 7 尺 B． 16 29 尺 C． 8 15 尺 D．16 31 尺 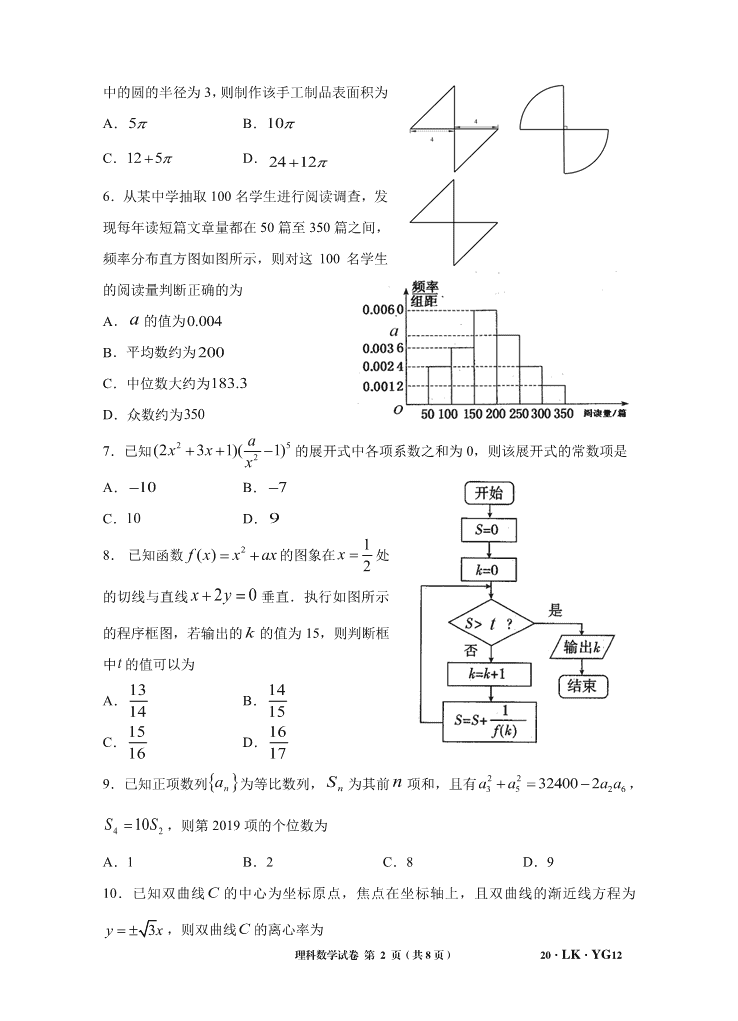5．某兴趣小组合作制作了一个手工制品，并将其绘制成如图所示的三视图，其中侧视图 考试开始前请勿填写 班级 姓名 准考 证号 考场号 座位号 理科数学试卷 第 2 页（共 8 页） 20·LK·YG12 中的圆的半径为 3，则制作该手工制品表面积为 A．5 B．10 C．12 5+ D． 24 12+ 6．从某中学抽取 100 名学生进行阅读调查，发 现每年读短篇文章量都在 50 篇至 350 篇之间， 频率分布直方图如图所示，则对这 100 名学生 的阅读量判断正确的为 A． a 的值为0.004 B．平均数约为 200 C．中位数大约为183.3 D．众数约为350 7．已知 25 2(2 3 1)( 1)axx x+ + − 的展开式中各项系数之和为 0，则该展开式的常数项是 A． 10− B． 7− C．10 D． 9 8． 已知函数 2()f x x ax=+的图象在 1 2x = 处 的切线与直线 20xy+=垂直．执行如图所示 的程序框图，若输出的 k 的值为 15，则判断框 中t 的值可以为 A． 13 14 B．14 15 C． 15 16 D． 16 17 9．已知正项数列 na 为等比数列， nS 为其前 n 项和，且有 22 3 5 2 632400 2a a a a+ = − ， 24 10SS = ，则第 2019 项的个位数为 A．1 B．2 C．8 D．9 10．已知双曲线 C 的中心为坐标原点，焦点在坐标轴上，且双曲线的渐近线方程为 3yx= ，则双曲线C 的离心率为 理科数学试卷 第 3 页（共 8 页） 20·LK·YG12 A． 2 B． 3 C． 3 或 32 2 D． 2 或 23 3 11．已知函数 )2,0)(sin(2)(  += xxf 在 ]3 2,2[ − 上至少存在两个不同的 21, xx 满足 4)()( 21 =xfxf ，且函数 )(xf 在 ]12,3[ − 上具有单调性， )0,6( − 和 12 7=x 分别为函数 图象的一个对称中心和一条对称轴，则下列命题中正确的是 A．函数 图象的两条相邻对称轴之间的距离为 4  B．函数 图象关于直线 3 −=x 对称 C．函数 图象关于点 )0,12( − 对称 D．函数 在 )2,6(  上是单调递减函数 12．已知函数 ()fx在(0,1) 恒有 ( ) 2 ( )xf x f x  ，其中 ()fx 为函数 ()fx的导数，若 ,为 锐角三角形的两个内角，则 A． )(sinsin)(sinsin 22  ff  B． )(cossin)(sincos 22  ff  C． )(coscos)(coscos 22  ff  D． )(cossin)(cossin 22  ff  二、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 13．设 ,xy满足约束条件 0 2 3 6 0 3 2 6 0 x y k xy xy − +   + −   − +  ，若目标函数 2z x y=− 的最大值与最小值之 和为 40 13− ，则 k =_______． 14．| | 2a = r ，| | 1b = r ， a r ， b r 的夹角为60，则 与 2ab− rr 的夹角为 ． 15．在三棱锥 P ABC− 中， 2 2, 4, 3, 5PA PB AB BC AC= = = = = ，若平面 PAB ⊥ 平面 ABC ，则三棱锥 P ABC− 外接球的表面积为_______． 理科数学试卷 第 4 页（共 8 页） 20·LK·YG12 16．已知抛物线 2:4C x y= ，任意直线 : ( 0)l y kx b b= +  ，已知直线l 交抛物线C 于 M ，N 两点，P 为 y 轴上的一点满足 OPM OPN =  （点O 为坐标原点），则 P 点 的坐标为_______． 三、解答题：本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．（ 12 分）在 ABC 中，内角 A ， B ， C 所对的边分别为 a ， b ， c ．已知 CaAca coscos2 =− ．求 b a 的值及角 的取值范围． 18．（ 12 分）如图，在平面多边形 SABCD 中，SA AD⊥ ， 1 2SA AB AD CD BC= = = = ， 3ABC =，以 AD 为折痕把 SAD 折起，使点 S 到达点 P 的位置，且 PA AB⊥ ，连 接 AC ． （1）求证：平面 PAC ⊥平面 PAB ； （2）求平面 PAB 与平面 PCD所成二面角的余弦值． 理科数学试卷 第 5 页（共 8 页） 20·LK·YG12 19．（ 本题满分 12 分） 某研究公司为了调查公众对某事件的关注程度，在某年的连续 6 个月内，月份 ix 和关注 人数 iy （单位：百）( 1,2,3, ,6)i = L 数据做了初步处理，得到下面的散点图及一些统计 量的值． （1）由散点图看出，可用线性回归模型拟合 y 与 x 的关系，请用相关系数加以说明， 并建立 y 关于 x 的回归方程； （2）经统计，调查材料费用 （单位：百元）与调查人数满足函数关系 1863 23 yv y=+ ， 求材料费用的最小值，并预测此时的调查人数； （3）现从这 6 个月中，随机抽取 3 个月份，求关注人数不低于 1600 人的月份个数 分 布列与数学期望． 参考公式：相关系数 n 1 n 22 11 )( ) ) ( ) ii i n ii ii x x y y r x x y y = == −− = −−   （ （ ，若 0.95r  ，则 与 的线性相关 程度相当高，可用线性回归模型拟合 与 的关系．回归方程 ˆˆ ˆy bx a=+中斜率与截距 理科数学试卷 第 6 页（共 8 页） 20·LK·YG12 的最小二乘估计公式分别为 6 1 6 2 1 () ) ˆ () ( ii i i i x x y y xx b = = − = −−  ， ˆˆa y bx=− ． 20．（ 本题满分 12 分） 已知椭圆 22 22: 1( 0)xyE a bab+ =   左、右焦点分别为 1F 、 2F ，上顶点为 A ，离心率 为 2 2 ， 1b = ． （1）求 E 的方程； （2）直线l 与 E 相切于点 P ，直线 m 过点 经点 P 被直线 反射得反射光线 n ．问： 直线 n 是否经过 x 轴上一个定点？若经过，求出该点的坐标；若不经过，说明理由． 理科数学试卷 第 7 页（共 8 页） 20·LK·YG12 21．（ 本题满分 12 分） 已知函数 ( ) ( 1) ( 0)xf x A x e A= +  ． （1）讨论函数 ()fx的单调性； （ 2 ）当 0A  时 ， 令 函 数 ( ) ( 1)x kxg x e e k x= + − + ，当 0x  时 ， 恒 有 2( ( )) ( 4 )g f x g x x+，求实数 A 的取值范围． 理科数学试卷 第 8 页（共 8 页） 20·LK·YG12 选考题：请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分。 22．【选修 4-4：坐标系与参数方程】（10 分） 在直角坐标系 xOy 中，直线l 的参数方程为 1 cos 2 sin xt yt   =+  =+ （t 为参数）．以坐标原点为极 点，以 x 轴 的 正 半 轴 为 极 轴 ， 建 立 极 坐 标 系 ， 曲 线 C 的 极 坐 标 方 程 为 2cos 4sin 0  + − = ． （1）求曲线 的普通方程； （2）已知 (1,2)M ，直线l 与曲线C 交于 P ，Q 两点，求 22MP MQ+ 的最大值． 23．【选修 4-5：不等式选讲】（10 分） 已知函数 21)( ++−= xxxf ． （1）求不等式 03)( −− xxf 的解集； （2）设函数 22)()( +−= xxfxg ，若存在 x 使 2( ) 2gx −成立，求实数  的取值 范围．