【精品试题】2021年高考数学一轮复习创优测评卷（新高考专用）测试卷03 三角函数（原卷版） 6页

2021 年高考数学一轮复习三角函数创优测评卷(新高考专用) 一、单选题（共 60 分，每题 5 分） 1．现有下列三角函数：① 4πsin π ( )3n n     Z ；②sin 2 ( )3n n     Z ；③ sin (2 1) ( )6n n      Z ；④sin (2 1) ( )3n n      Z ．其中函数值与 πsin 3 的值相同的是（ ） A．①② B．②④ C．①③ D．①②④ 2．下列三角函数值的符号判断正确的是（ ） A．sin156 0 B． 16cos 05   C． 17tan 08      D． tan556 0 3．有如下关于三角函数的四个命题： 1 :p x R  ， 2 2 1sin cos2 2 2 x x  2 : ,p x y R  ，  sin sin sinx y x y    3 : 0,πp x  ， 1 cos2 sin2 x x  4 :p 若sin cosx y ，则 π 2x y  其中假命题的是（ ） A． 1p ， 4p B． 2p ， 4p C． 1p ， 3p D． 2p ， 4p 4．依据三角函数线，作出如下四个判断： ① π 6πsin sin5 5  ；② π πcos cos4 4      ；③ π 3πtan tan8 8  ；④ 3π 4πsin sin5 5  . 其中判断正确的有( ) A．1 个 B．2 个 C．3 个 D．4 个 5．已知某三角函数的部分图象如图所示，则它的解析式可能是（ ） A． sin( )4y x   B． 3sin(2 )4y x   C． cos( )4y x   D． 3cos(2 )4y x   6．将三角函数 sin 2 6y x      向左平移 6  个单位后，得到的函数解析式为 （ ） A．sin 2 6x     B．sin 2 3x     C． sin 2x D． cos2x 7．三角函数是刻画客观世界周期性变化规律的数学模型，单位圆定义法是任意角的三角函数常用的定义方 法，是以角度（数学上最常用弧度制）为自变量，任意角的终边与单位圆交点坐标为因变量的函数.平面直 角坐标系中的单位圆指的是平面直角坐标系上，以原点为圆心，半径为单位长度的圆.问题：已知角 的终 边与单位圆的交点为 3 4,5 5P    ，则 cos( ) sin( )      （ ） A． 1 5  B． 1 5 C． 7 5  D． 7 5 8．欧拉公式 cos sinixe x i x  （i 为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩 大到复数，建立了三角函数和指数函数的关系，根据欧拉公式可知， 4 i i e e   表示的复数在复平面中位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 9．数学家托勒密从公元127 年到151年在亚历山大城从事天文观测，在编制三角函数表过程中发现了很多 重要的定理和结论，如图便是托勒密推导倍角公式“ 22 1 2cos a sin a  ”所用的几何图形，已知点 ,B C 在 以线段 AC 为直径的圆上， D 为弧 BC 的中点，点 E 在线段 AC 上且 ,AE AB 点 F 为 EC 的中点.设 2 ,AC r ,DAC a  那么下列结论: 2 ,DC rcosa① 2 2 ,AB rcos a②  1 2 ,FC r cos a ③  2 2DC r r AB ④ . 其中正确的是（ ） A． ②③ B． ②④ C． ①③④ D． ②③④ 10．关于三角函数的图像，有下列命题：① sin | |y x 与 siny x 的图像关于 y 轴对称；② siny x  与 | sin |y x 的图像关于 x 轴对称；③ cos( )y x  与 cos | |y x 的图像重合；④ sin cosy x x  的图像关 于原点对称．其中错误命题的个数是（ ） A．1 个 B．2 个 C．3 个 D．4 个 11．为了研究钟表与三角函数的关系，建立如图所示的平面直角坐标系，设秒针针尖指向位置  ,P x y .若 初始位置为 0 3 1,2 2P       ，秒针从 0P （注：此时 0t  ）开始沿顺时针方向走动，则点 P 的纵坐标 y 与时间t 的函数关系式为（ ） A． sin 30 6y t      B． sin 60 6y t       C． sin 30 6y t       D． sin 30 6y t       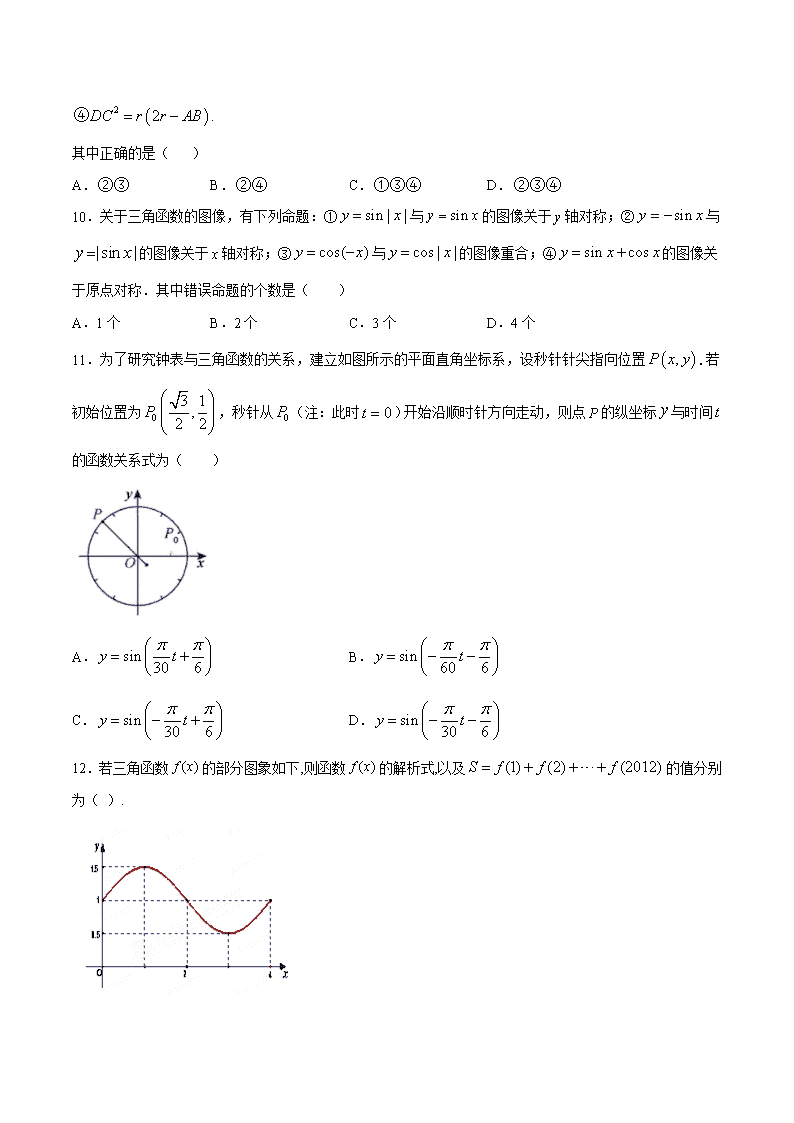12．若三角函数 ( )f x 的部分图象如下,则函数 ( )f x 的解析式,以及 (1) (2) (2012)S f f f    的值分别 为（ ）. A． 1( ) sin 12 2 xf x   , 2012S  B． 1( ) cos 12 2 xf x   , 2012S  C． 1( ) sin 12 2 xf x   , 2012.5S  D． 1( ) cos 12 2 xf x   , 2012.5S  二、填空题（共 20 分，每题 5 分） 13．对函数 ( )f x ,若      , , , , ,a b c R f a f b f c  为某一个三角形的边长，则称  f x 为“ 三角函数”， 已知函数   1 x x e mf x e   为“ 三角函数”，则实数 m 的取值范围是__________ 14．如图，在直三棱柱 1 1 1ABC A B C 中， =90ACB  ， 4AC  ， 3BC  ， 1AB BB ，则异面直线 1A B 与 1 1B C ，所成角的大小是___________（结果用反三角函数表示）． 15． ABC 中，角 , ,A B C 所对的边分别为 , ,a b c ，向量 (2 ,1)q a ， (2 ,cos )p b c C  ，且 / /p q   ，三角 函数式 2cos2 11 tan C C    的取值范围是 . 16．欧拉公式 ie cos isin    ，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的联系， 被誉为“数学中的天桥”，已知数列{ }na 的通项公式为 cos 2020n na   isin 2020 n （ 1,2,3,n   ），则数 列{ }na 前 2020 项的乘积为________ 三、解答题（共 70 分） 17．（10 分）已知 17tan 4 7        ; （1）求 tan 以及 2sin 2 cos 1 cos2      的值; （2）若 0 ,02 2       ，且 16cos( ) 65     ，求  的值（用反三角函数表示）. 18．（12 分）在四棱锥 P ABCD 中，底面正方形 ABCD 的边长为 2，PA  底面 ABCD ，E 为 BC 的中 点， PC 与平面 PAD 所成的角为 2arctan .2 （1）求 PA 的长度； （2）求异面直线 AE 与 PD 所成角的大小．(结果用反三角函数表示) 19．（12 分）如图，在梯形 ABCD 中，AD ∥ BC ， 90ABC  ，AB a= ， 3AD a ，且 2 5arcsin 5ADC  ， 又 PA  平面 ABCD ， AP a . 求：（1）二面角 P CD A  的大小（用反三角函数表示）； （2）点 A 到平面 PBC 的距离. 20．（10 分）已知角 是第二象限角，其终边与以原点为圆心的单位圆交于点 12 5,13 13P    . （1）写出三角函数 ,cossin  的值； （2）求     tan2 cos sin sin              的值. 21 ． （ 12 分 ） 已 知 a b c， ， 分 别 是 ABC△ 的 内 角 A B C， ， 所 对 的 边 长 ， 且 a c ， 满  cos cos 3 sin cos 0C A A B   ． （1）求角 B 的大小； （2）若点 O 是 ABC△ 外一点， 2 4OA OB  ，记 AOB   ，用含 的三角函数式表示平面四边形OACB 面积并求面积的最大值． 22．（14 分）已知向量 (2 0)OB  ， ，向量 (2 2)OC  ， ，向量 ( 2 cos , 2 sin )CA   ，记OB 与OC 的 夹角为 ． (Ⅰ)求 3sin( ) cos 2 cos tan( )2                   (Ⅱ)求向量OA 与向量 OB 的夹角的取值范围．