高考数学总复习课时规范练19函数y=Asin(ωxφ)的图象及应用文新人教A版 9页

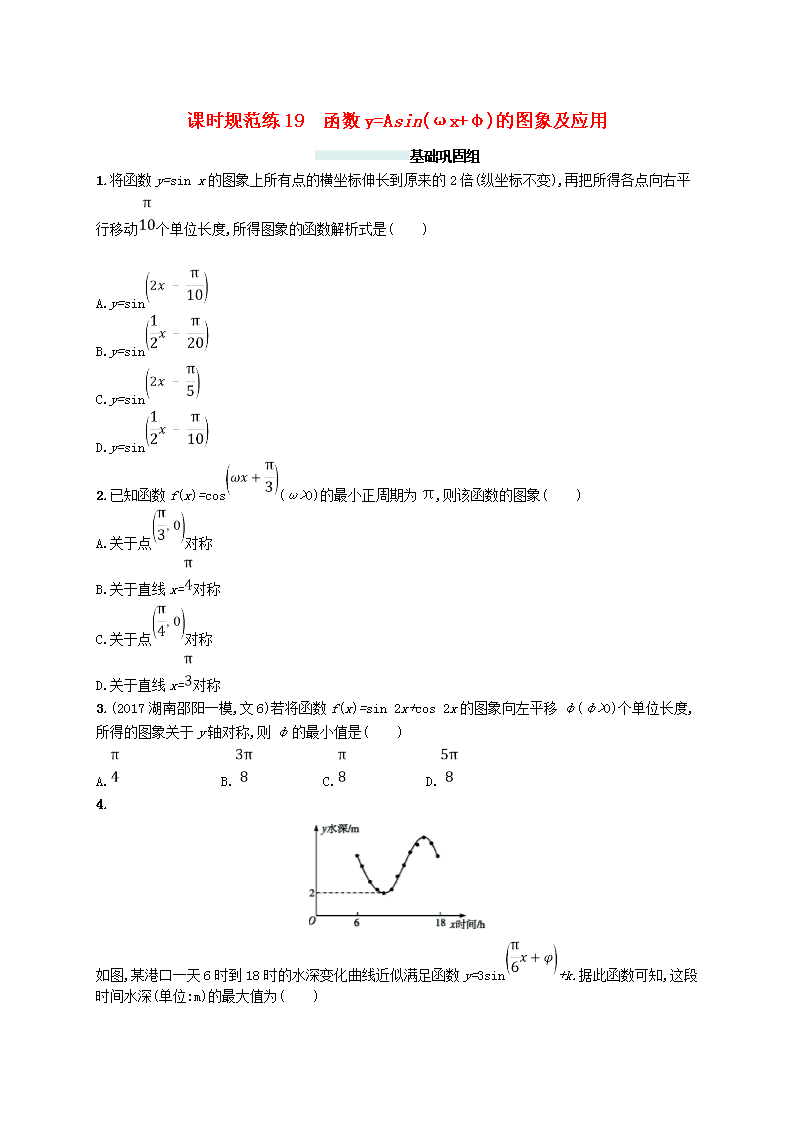
课时规范练 19 函数 y=Asin(ωx+φ)的图象及应用 基础巩固组 1.将函数 y=sin x 的图象上所有点的横坐标伸长到原来的 2 倍(纵坐标不变),再把所得各点向右平 行移动 个单位长度,所得图象的函数解析式是( ) A.y=sin B.y=sin C.y=sin D.y=sin 2.已知函数 f(x)=cos (ω>0)的最小正周期为π,则该函数的图象( ) A.关于点 对称 B.关于直线 x= 对称 C.关于点 对称 D.关于直线 x= 对称 3.(2017 湖南邵阳一模,文 6)若将函数 f(x)=sin 2x+cos 2x 的图象向左平移φ(φ>0)个单位长度, 所得的图象关于 y 轴对称,则φ的最小值是( ) A. B. C. D. 4. 如图,某港口一天 6 时到 18 时的水深变化曲线近似满足函数 y=3sin +k.据此函数可知,这段 时间水深(单位:m)的最大值为( ) A.5 B.6 C.8 D.10 5.(2017 天津,文 7)设函数 f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π,若 f =2,f =0,且 f(x)的最小正周期大于 2π,则( ) A.ω= ,φ= B.ω= ,φ=- C.ω= ,φ=- D.ω= ,φ= 〚导学号 24190738〛 6.若函数 f(x)=2sin 2x 的图象向右平移φ 个单位长度后得到函数 g(x)的图象,若对满 足|f(x1)-g(x2)|=4 的 x1,x2,有|x1-x2|的最小值为 ,则φ=( ) A. B. C. D. 7. 已知函数 f(x)=sin(ωx+φ) 的部分图象如图所示,则 y=f 取得最小值时 x 的 集合为( ) A. B. C. D. 〚导学号 24190739〛 8.函数 y=sin x- cos x 的图象可由函数 y=2sin x 的图象至少向右平移 个单位长度得 到. 9. 已知函数 y=g(x)的图象由 f(x)=sin 2x 的图象向右平移φ(0<φ<π)个单位长度得到,这两个函数 的部分图象如图所示,则φ= . 10.(2017 北京,文 16)已知函数 f(x)= cos -2sin xcos x. (1)求 f(x)的最小正周期; (2)求证:当 x∈ 时,f(x)≥- . 〚导学号 24190740〛 综合提升组 11.(2017 辽宁大连一模,文 11)若关于 x 的方程 2sin =m 在 上有两个不等实根,则 m 的 取值范围是( ) A.(1, ) B.[0,2] C.[1,2) D.[1, ] 12.已知函数 f(x)=cos(2x+φ)的图象关于点 对称,若将函数 f(x)的图象向右平移 m(m>0)个 单位长度后得到一个偶函数的图象,则实数 m 的最小值为 . 13.已知函数 y=3sin . (1)用五点法作出函数的图象; (2)说明此图象是由 y=sin x 的图象经过怎么样的变化得到的. 〚导学号 24190741〛 创新应用组 14.已知曲线 C1:y=cos x,C2:y=sin ,则下面结论正确的是( ) A.把 C1 上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得 到曲线 C2 B.把 C1 上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得 到曲线 C2 C.把 C1 上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到 曲线 C2 D.把 C1 上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得 到曲线 C2〚导学号 24190742〛 15.如图所示,某地夏天 8—14 时用电量变化曲线近似满足函数式 y=Asin(ωx+φ)+b,ω>0,φ∈ (0,π). (1)求这期间的最大用电量及最小用电量; (2)写出这段曲线的函数解析式. 答案： 1.B 由题意,y=sin x 的图象进行伸缩变换后得到 y=sin x 的图象,再进行平移后所得图象的函数 为 y=sin =sin .故选 B. 2.D 由题意知ω=2,函数 f(x)的对称轴满足 2x+ =kπ(k∈Z),解得 x= (k∈Z),当 k=1 时,x= , 故选 D. 3.C 函数 f(x)=sin 2x+cos 2x= sin 的图象向左平移φ个单位长度,所得函数 y= sin 的图象关于 y 轴对称, 则有 2φ+ =kπ+ ,k∈Z. 解得φ= kπ+ ,k∈Z. 由φ>0,则当 k=0 时,φ的最小值为 .故选 C. 4.C 因为 sin ∈[-1,1],所以函数 y=3sin +k 的最小值为 k-3,最大值为 k+3. 由题图可知函数最小值为 k-3=2,解得 k=5. 所以 y 的最大值为 k+3=5+3=8,故选 C. 5.A 由题意可知, >2π, , 所以 ≤ω<1.所以排除 C,D. 当ω= 时,f =2sin =2sin =2, 所以 sin =1. 所以 +φ= +2kπ,即φ= +2kπ(k∈Z). 因为|φ|<π,所以φ= .故选 A. 6.C 由函数 f(x)=2sin 2x 的图象向右平移φ 个单位长度后得到函数 g(x)=2sin[2(x- φ)]的图象,可知对满足|f(x1)-g(x2)|=4 的 x1,x2,有|x1-x2|的最小值为 -φ.故 -φ= ,即φ= . 7.B 根据所给图象,周期 T=4× =π,故π= ,即ω=2,因此 f(x)=sin(2x+φ). 又图象经过 ,代入有 2× +φ=kπ(k∈Z), 再由|φ|< ,得φ=- , 故 f =sin ,当 2x+ =- +2kπ(k∈Z),即 x=- +kπ(k∈Z)时,y=f 取得最小值. 8. 因为 y=sin x- cos x=2sin ,所以函数 y=sin x- cos x 的图象可由函数 y=2sin x 的图象至少向右平移 个单位长度得到. 9. 函数 f(x)=sin 2x 的图象在 y 轴右侧的第一个对称轴为 2x= ,则 x= . x= 关于 x= 对称的直线为 x= ,由图象可知,通过向右平移之后,横坐标为 x= 的点平移到 x= ,则φ= . 10.(1)解 f(x)= cos 2x+ sin 2x-sin 2x = sin 2x+ cos 2x =sin . 所以 f(x)的最小正周期 T= =π. (2)证明 因为- ≤x≤ , 所以- ≤2x+ . 所以 sin ≥sin =- . 所以当 x∈ 时,f(x)≥- . 11.C 方程 2sin =m 可化为 sin ,当 x∈ 时,2x+ , 画出函数 y=f(x)=sin 在 x∈ 上的图象如图所示. 由题意,得 <1,即 1≤m<2,∴m 的取值范围是[1,2),故选 C. 12. ∵函数的图象关于点 对称,∴2× +φ=kπ+ ,k∈Z, 解得φ=kπ- ,k∈Z, ∴f(x)=cos ,k∈Z. ∵f(x)的图象平移后得函数 y=cos (k∈Z)为偶函数,∴-2m+kπ- =k1π(k∈Z,k1∈Z),m= . ∵m>0,∴m 的最小正值为 ,此时 k-k1=1(k∈Z,k1∈Z). 13.解 (1)列表: x x- 0 π π 2 π 3sin 0 3 0 -3 0 描点、连线,如图所示. (2)(方法一)“先平移,后伸缩”. 先把 y=sin x 的图象上所有点向右平移 个单位长度,得到 y=sin 的图象,再把 y=sin 的图象上所有点的横坐标伸长到原来的 2 倍(纵坐标不变),得到 y=sin 的图象, 最后将 y=sin 的图象上所有点的纵坐标伸长到原来的 3 倍(横坐标不变),就得到 y=3sin 的图象. (方法二)“先伸缩,后平移” 先把 y=sin x 的图象上所有点的横坐标伸长到原来的 2 倍(纵坐标不变),得到 y=sin x 的图象, 再把 y=sin x 图象上所有的点向右平移 个单位长度,得到 y=sin =sin 的图象,最 后将 y=sin 的图象上所有点的纵坐标伸长到原来的 3 倍(横坐标不变),就得到 y=3sin 的图象. 14.D 曲线 C1 的方程可化为 y=cos x=sin ,把曲线 C1 上各点的横坐标缩短到原来的 倍,纵坐 标不变,得曲线 y=sin =sin 2 ,为得到曲线 C2:y=sin 2 ,需再把得到的曲线向左 平移 个单位长度. 15.解 (1)由图象,知这期间的最大用电量为 50 万千瓦时,最小用电量为 30 万千瓦时. (2)A= (50-30)=10,b= (50+30)=40, T= =2×(14-8)=12, 所以ω= , 所以 y=10sin +40. 把 x=8,y=30 代入上式,得φ= .所以所求解析式为 y=10sin +40,x∈[8,14].