专题45 立体几何中的向量方法（二）—求空间角和距离-2020年领军高考数学一轮复习（文理通用） Word版含解析 62页

专题45立体几何中的向量方法（二）——求空间角和距离 最新考纲 ‎1.能用向量方法解决直线与直线、直线与平面、平面与平面所成角的计算问题．‎ ‎2.了解向量方法在研究立体几何问题中的应用.‎ 基础知识融会贯通 ‎1．两条异面直线所成角的求法 设a，b分别是两异面直线l1，l2的方向向量，则 l1与l2所成的角θ a与b的夹角β 范围 ‎[0，π]‎ 求法 cos θ＝ cos β＝ ‎2.直线与平面所成角的求法 设直线l的方向向量为a，平面α的法向量为n，直线l与平面α所成的角为θ，a与n的夹角为β，则sin θ＝|cos β|＝.‎ ‎3．求二面角的大小 ‎(1)如图①，AB，CD分别是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈，〉．‎ ‎(2)如图②③，n1，n2分别是二面角α－l－β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|cos〈n1，n2〉|，二面角的平面角大小是向量n1与n2的夹角(或其补角)．‎ ‎【知识拓展】‎ 利用空间向量求距离(供选用)‎ ‎(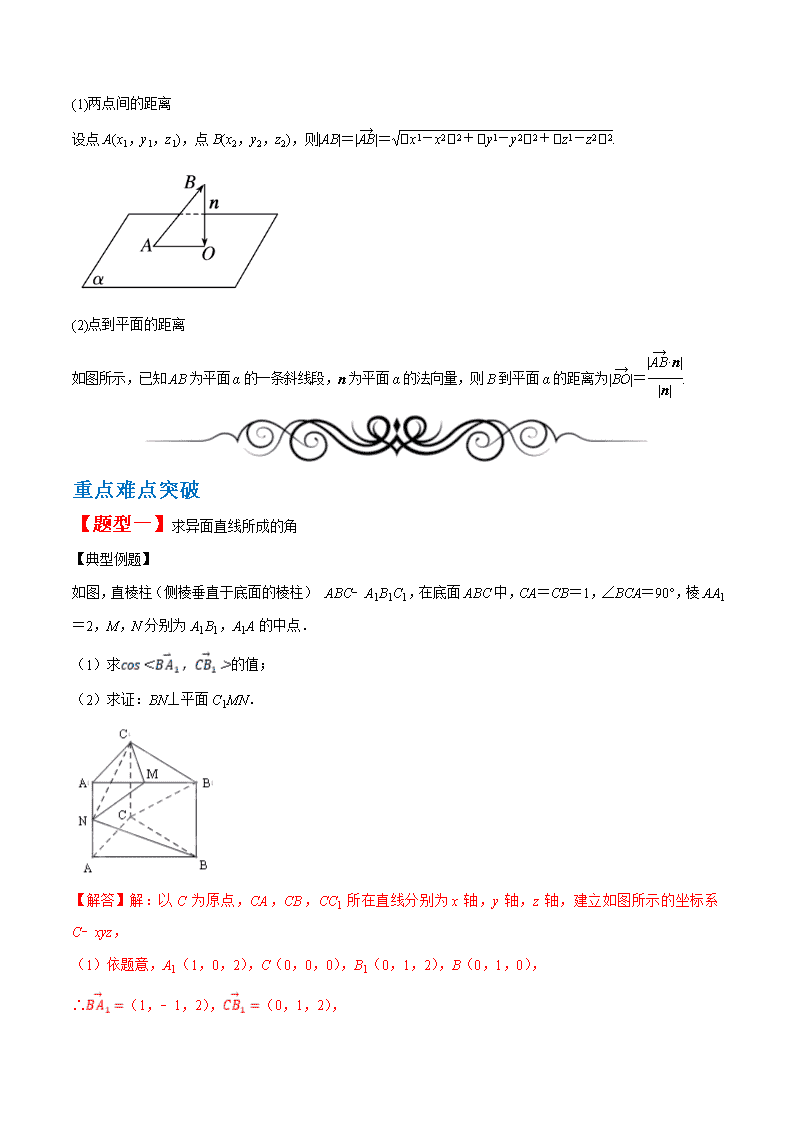1)两点间的距离 设点A(x1，y1，z1)，点B(x2，y2，z2)，则|AB|＝||＝.‎ ‎(2)点到平面的距离 如图所示，已知AB为平面α的一条斜线段，n为平面α的法向量，则B到平面α的距离为||＝.‎ 重点难点突破 ‎【题型一】求异面直线所成的角 ‎【典型例题】‎ 如图，直棱柱（侧棱垂直于底面的棱柱） ABC﹣A1B‎1C1，在底面ABC中，CA＝CB＝1，∠BCA＝90°，棱AA1＝2，M，N分别为A1B1，A‎1A的中点．‎ ‎（1）求的值； ‎ ‎（2）求证：BN⊥平面C1MN．‎ ‎【解答】解：以C为原点，CA，CB，CC1所在直线分别为x轴，y轴，z轴，建立如图所示的坐标系C﹣xyz，‎ ‎（1）依题意，A1（1，0，2），C（0，0，0），B1（0，1，2），B（0，1，0），‎ ‎∴（1，﹣1，2），（0，1，2），‎ ‎∴•1×0+（﹣1）×1+2×2＝3，‎ 又||，||，‎ ‎∴cos，6分 证明：（2）A1（1，0，2），C1（0，0，2），B1（0，1，2），N（1，0，1），‎ ‎∴M（，，2），∴（，，2），（1，0，﹣1），（1，﹣1，1），‎ ‎∴•1（﹣1）+1×0＝0，同理可求•0，‎ ‎∴⊥，⊥，C‎1M∩C1N＝C1，‎ ‎∴BN⊥平面C1MN…12分．‎ ‎ 【再练一题】‎ 如图，BC＝2，原点O是BC的中点，点A的坐标为（，，0），点D在平面yOx上，且∠BDC＝90°，∠DCB＝30°．‎ ‎（1）求向量的坐标．‎ ‎（2）求与的夹角的余弦值．‎ ‎【解答】解：（1）过D作DE⊥BC于E，则DE＝CD•sin30°，‎ OE＝OB﹣BDcos60°＝1，‎ ‎∴D的坐标为D（0，，，‎ 又∵C（0，1，0），∴（0，，）．‎ ‎（2）依题设有A点坐标为A（，，0），‎ ‎∴（），（0，2，0），‎ 则与的夹角的余弦值：‎ cos．‎ ‎ 思维升华 用向量法求异面直线所成角的一般步骤 ‎(1)选择三条两两垂直的直线建立空间直角坐标系；‎ ‎(2)确定异面直线上两个点的坐标，从而确定异面直线的方向向量；‎ ‎(3)利用向量的夹角公式求出向量夹角的余弦值；‎ ‎(4)两异面直线所成角的余弦值等于两向量夹角余弦值的绝对值．‎ ‎【题型二】求直线与平面所成的角 ‎【典型例题】‎ 如图所示，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，BC＝BAAD＝m，VA⊥平面ABCD．‎ ‎（1）求证：CD⊥平面VAC；‎ ‎（2）若VAm，求CV与平面VAD所成角的大小．‎ ‎【解答】（1）证明：连结AC，∵AB＝BC，∠ABC＝90°，∴∠CAB＝∠ACB＝45°，‎ 取AD中点G，连CG，因为BC∥AD，所以四边形ABCG为正方形．‎ 所以CG＝GD，∠CGD＝90°，∴∠DCG＝45°，‎ ‎∴∠DCA＝90°……………………‎ 所以CD⊥CA，‎ 又VA⊥平面ABCD，所以CD⊥VA，‎ CD⊥平面VAC………………‎ ‎（2）解：法1：连VG 由⇒CG⊥面VAD，∴∠CVG是CV与平面VAD所成的角………………‎ VC‎2m；CG＝m，∴∠CVG＝30°‎ ‎∴CV与平面VAD所成角为30°………………‎ 法2：以A为原点，射线AB，AD，AV所在直线为x，y，z轴正半轴，建立空间直角坐标系，则平面VAD法向量（m，0，0），又，设向量与夹角为θ，则cosθ，θ，CV与平面VAD所成的角为．‎ ‎ 【再练一题】‎ 如图，四棱锥P﹣ABCD中，底面为直角梯形，AB∥CD，∠BAD＝90°，AB＝2CD＝4，PA⊥CD，在锐角△PAD中，E是边PD上一点，且AD＝PD＝3ED．‎ ‎（1）求证：PB∥平面ACE；‎ ‎（2）当PA的长为何值时，AC与平面PCD所成的角为30°？‎ ‎【解答】（1）证明：连接BD交AC于O，‎ ‎∵AB∥CD，∴△OCD∽△OAB，‎ ‎∴，又，‎ ‎∴OE∥PB，又OE⊂平面ACE，PB⊄平面ACE，‎ ‎∴PB∥平面ACE．‎ ‎（2）解：过A作AF⊥PD，垂足为F，连接CF，‎ ‎∵CD⊥AD，CD⊥PA，PA∩AD＝A，‎ ‎∴CD⊥平面PAD，∴CD⊥AF，‎ 又AF⊥PD，PD∩CD＝D，‎ ‎∴AF⊥平面PCD，∴∠ACF为AC与平面PCD所成的角，即∠ACF＝30°．‎ AC，∴AFAC，‎ ‎∴sin∠ADF，cos∠ADF，‎ ‎∴PA．‎ ‎∴当PA时，AC与平面PCD所成的角为30°．‎ ‎ 思维升华 利用向量法求线面角的方法 ‎(1)分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；‎ ‎(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角．‎ ‎【题型三】求二面角 ‎【典型例题】‎ 四棱锥P﹣ABCD中，平面PCD⊥平面ABCD，四边形ABCD为矩形，AB＝4，AD＝3，∠PAB＝90°．‎ ‎（1）求证：PD⊥平面ABCD；‎ ‎（2）若直线BD与平面PAB所成角的正弦值为，求二面角C﹣PA﹣D的余弦值．‎ ‎【解答】证明：（1）因为平面PCD⊥平面ABCD，且∠BCD＝90°．‎ 所以BC⊥平面PCD，所以PD⊥BC．‎ 又因为AB⊥PA，AB⊥AD，‎ 所以AB⊥平面PAD，所以PD⊥AB．‎ 又因为PD⊥BC，所以PD⊥平面ABCD．‎ 解：（2）以D为原点，DA，DP，DC方向分别为x轴，y轴，z轴正方向建立如图空间直角坐标系．‎ 作DE⊥PA于E，连接BE，‎ 因为平面PAD⊥平面PAB，‎ 所以DE⊥平面PAB，∠DBE即为直线BD与平面PAB所成的角，‎ 故，所以DE．‎ Rt△PAD中，令PD＝x，则x•3•，‎ 解得x＝3，故A（3，0，0），P（0，3，0），C（0，0，4）．‎ ‎（﹣3，3，0），（﹣3，0，4），‎ 设平面PAC的一个法向量为（a，b，c），‎ 则，取（4，4，3）．‎ 又因为平面PAD的一个法向量为（0，0，4），‎ 故cos．‎ 综合图形可知，所求二面角的余弦值为．‎ ‎ 【再练一题】‎ 如图在直角△ABC中，B为直角，AB＝2BC，E，F分别为AB，AC的中点，将△AEF沿EF折起，使点A到达点D的位置，连接BD，CD，M为CD的中点．‎ ‎（Ⅰ）证明：MF⊥面BCD；‎ ‎（Ⅱ）若DE⊥BE，求二面角E﹣MF﹣C的余弦值．‎ ‎【解答】证明：（Ⅰ）取DB中点N，连结MN、EN，‎ ‎∵MN，EF，‎ ‎∴四边形EFMN是平行四边形，‎ ‎∵EF⊥BE，EF⊥DE，BE∩EF＝E，‎ ‎∴EF⊥平面BDE，‎ ‎∴EF⊥EN，∴MF⊥MN，‎ 在△DFC中，DF＝FC，‎ 又∵M为CD的中点，∴MF⊥CD，‎ 又∵MF∩MN＝M，∴MF⊥平面BCD．‎ 解：（Ⅱ）∵DE⊥BE，DE⊥EF，BE∩EF＝E，‎ ‎∴DE⊥平面BEF，‎ 以E为原点，BE、EF、ED所在直线分别为x，y，z轴，建立空间直角坐标系，‎ 设BC＝2，则E（0，0，0），F（0，1，0），C（﹣2，2，0），M（﹣1，1，1），‎ ‎∴（0，1，0），（﹣1，0，1），（2，﹣1，0），‎ 设面EMF的法向量（x，y，z），‎ 则，取x＝1，得（1，0，1），‎ 同理，得平面CMF的法向量（1，2，1），‎ 设二面角E﹣MF﹣C的平面角为θ，‎ 则cosθ，‎ ‎∴二面角E﹣MF﹣C的余弦值为．‎ ‎ 思维升华 利用向量法计算二面角大小的常用方法 ‎(1)找法向量法：分别求出二面角的两个半平面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角的大小．‎ ‎(2)找与棱垂直的方向向量法：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小．‎ ‎【题型四】求空间距离 ‎【典型例题】‎ 四棱锥P﹣ABCD中，底面ABCD是菱形，∠BAD＝60°，PA＝PB＝PD．‎ ‎（1）求证：PD⊥AB；‎ ‎（2）若AB＝6，PC＝8，E是BD的中点，求点E到平面PCD的距离．‎ ‎【解答】（1）证明：由于四边形ABCD是菱形，∠BAD＝60°，所以△ABD是正三角形．‎ 设AB的中点为K，连接PK，DK，如图所示，则AB⊥DK，‎ 又PA＝PB，所以AB⊥PK．‎ 又PK，DK相交于K，所以AB⊥平面PKD．‎ 又PD⊂平面PKD，所以AB⊥PD．‎ ‎（2）解：由（1）可知，AB⊥平面PKD．‎ 又AB∥CD，所以CD⊥平面PKD．‎ 又CD⊂平面PDC，所以平面PDC⊥平面PKD，‎ 设点E到平面PCD的距离为h，则由于BD＝2ED，得点B到平面PCD的距离为2h．‎ 由于KB∥平面PCD，所以K，B两点到平面PCD的距离均为2h．‎ 所以点K到直线PD的距离就是2h．设△ABD的中心为H，则PH⊥平面ABD．‎ HC＝4HE＝4，在rt△PHC中，PH4，‎ 在Rt△PHD中，PH＝4，DH＝2，所以PD2．‎ 由DH＝2HK，得点H到直线PD的距离为，即，得h．‎ 所以点E到平面PCD的距离为．‎ ‎ 【再练一题】‎ 如图，PA⊥平面ABCD，四边形ABCD是正方形，PA＝AD＝2，M、N分别是A B．PC的中点．‎ ‎（1）求证：平面MND⊥平面PCD； ‎ ‎（2）求点P到平面MND的距离．‎ ‎【解答】解：（1）∵PA⊥平面ABCD，AB⊥AD，∴AB、AD、AP两两互相垂直，‎ 如图所示，分别以AB、AD、AP所在直线为x轴、y轴和z轴建立空间直角坐标系，可得A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），P（0，0，2），‎ M（1，0，0），N（1，1，1），‎ ‎∴（0，1，1），（﹣1，1，﹣1），（0，2，﹣2）‎ 设（x，y，z）是平面MND的一个法向量，‎ 可得，取y＝﹣1，得x＝﹣2，z＝1，‎ ‎∴（﹣2，﹣1，1）是平面MND的一个法向量，同理可得（0，1，1）是平面PCD的一个法向量，‎ ‎∵•2×0+（﹣1）×1+1×1＝0，∴，‎ 即平面MND的法向量与平面PCD的法向量互相垂直，可得平面MND⊥平面PCD；‎ ‎（2）由（1）得（﹣2，﹣1，1）是平面MND的一个法向量，‎ ‎∵（0，2，﹣2），得•0×（﹣2）+2×（﹣1）+（﹣2）×1＝﹣4，‎ ‎∴点P到平面MND的距离d．‎ ‎ 思维升华 求点面距一般有以下三种方法：‎ ‎(1)作点到面的垂线，点到垂足的距离即为点到平面的距离．‎ ‎(2)等体积法．‎ ‎(3)向量法．其中向量法在易建立空间直角坐标系的规则图形中较简便．‎ 基础知识训练 ‎1．【天津市部分区2019届高三联考一模】在如图所示的几何体中，四边形是正方形，四边形是梯形，∥，，平面平面，且.‎ ‎（Ⅰ）求证：∥平面；‎ ‎（Ⅱ）求二面角的大小；‎ ‎（Ⅲ）已知点在棱上，且异面直线与所成角的余弦值为，求线段的长．‎ ‎【答案】（1）证明见解析；（2）；（3）.‎ ‎【解析】‎ ‎（1）平面平面，‎ 平面平面 ，‎ ‎，，‎ 直线平面. ‎ 由题意，以点为原点，分别以的方向为轴，轴，轴的正向建立如图空间直角坐标系，‎ 则可得：，‎ ‎. ‎ 依题意，易证：是平面的一个法向量，‎ 又， ，‎ 又直线平面， . ‎ ‎（2） .‎ 设为平面的法向量，‎ 则，即.‎ 不妨设，可得. ‎ 设为平面的法向量，‎ 又 ，‎ 则，即.‎ 不妨设，可得， ‎ ‎ ，‎ 又二面角为钝二面角，‎ 二面角的大小为. ‎ ‎（3）设，则，又，‎ 又，即， ‎ ‎ ，解得或（舍去）.‎ 故所求线段的长为.‎ ‎2．【山东省淄博市部分学校2019届高三5月阶段性检测（三模)】已知正方形的边长为分别为的中点，以为棱将正方形折成如图所示的的二面角，点在线段上．‎ ‎（1）若为的中点，且直线，由三点所确定平面的交点为，试确定点的位置，并证明直线平面；‎ ‎（2）是否存在点，使得直线与平面所成的角为；若存在，求此时二面角的余弦值，若不存在，说明理由．‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ ‎（1）因为直线平面，‎ 故点在平面内也在平面内，‎ 所以点在平面与平面的交线上（如图所示）‎ 因为，为的中点，所以，‎ 所以，，所以点在的延长线上，且 连结交于，因为四边形为矩形，所以是的中点 连结，因为为的中位线，所以，‎ 又因为平面，所以直线平面.‎ ‎（2）由已知可得，，，所以平面，‎ 所以平面平面，取的中点为坐标原点，建立如图所示的空间直角坐标系，‎ 所以，，，，‎ 所以，，‎ 设，则，‎ 设平面的法向量，则，‎ 取，则，，所以，‎ 与平面所成的角为，所以，‎ 所以，所以，解得或，‎ 所以存在点，使得直线与平面所成的角为，‎ 取的中点，则为平面的法向量，因为，‎ 所以，，‎ 设二面角的大小为，‎ 所以，‎ 因为当时，，平面平面，‎ 所以当时，为钝角，所以.‎ 当时，为锐角，所以.‎ ‎3．【陕西省汉中市2019届高三全真模拟考试】如图，四边形为矩形，平面平面，，，，，点在线段上.‎ ‎（1）求证：平面；‎ ‎（2）若二面角的余弦值为，求的长度.‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎（1）证明：∵，∴，‎ 又平面平面，平面平面，平面，‎ ‎∴平面.‎ ‎（2）以为原点，以，，为，，轴建立如图所示的空间直角坐标系，‎ 则，，，，，‎ ‎∴，，‎ 由题知，平面，‎ ‎∴为平面的一个法向量，‎ 设，则，∴，‎ 设平面的一个法向量为，则，‎ ‎∴，令，可得，‎ ‎∴，得或（舍去），‎ ‎∴.‎ ‎4．【河南省八市重点高中联盟“领军考试”2019届高三第五次测评】如图，三棱柱中，平面平面，，.‎ ‎（1）求证：平面平面；‎ ‎（2）若与平面所成的线面角为，求二面角的余弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ ‎（1）因为平面平面，平面平面，‎ 平面，，所以平面，‎ 因为平面，所以.‎ 因为，所以.‎ 因为是平行四边形，且，所以是菱形，.‎ 因为，所以平面.‎ 又平面，所以平面平面.‎ ‎（2）取的中点，连接，因为是菱形，，‎ 所以是正三角形，所以，且.‎ 令，则.‎ 所以以为原点，以所在直线为轴，所在直线为轴，过点且平行于的直线为轴，建立如图所示的空间直角坐标系.‎ 则，，，，，，‎ ‎，.‎ 设平面的一个法向量为，则，‎ 所以，得，令，则，所以.‎ 由（1）知平面，所以是平面的一个法向量，‎ 所以.‎ 所以二面角的余弦值为.‎ ‎5．【辽宁省葫芦岛市普通高中2019届高三第二次模拟考试】如图，在多面体中，平面平面.四边形为正方形，四边形为梯形，且，是边长为1的等边三角形，M为线段中点，.‎ ‎(1)求证：； ‎ ‎(2)求直线与平面所成角的正弦值；‎ ‎(3)线段上是否存在点N，使得直线平面？若存在，求的值；若不存在，请说明理由.‎ ‎【答案】（1）见解析（2）（3）线段BD上存在点N,使得直线平面AFN，且 ‎，详见解析.‎ ‎【解析】‎ ‎(1)证明：因为为正方形，‎ 所以．‎ 又因为平面平面，‎ 且平面平面，‎ 所以平面．‎ 所以． ‎ ‎(2)取AD中点O,EF中点K，连接OB，OK.于是在△ABD中，，在正方ADEF中，又平面平面，故平面，进而，‎ 即两两垂直． ‎ 分别以为x轴，y轴,z轴 建立空间直角坐标系（如图）．‎ 于是，，,,,‎ 所以 设平面的一个法向量为，‎ 则 即 ‎ 令，则，则．‎ 设直线与平面所成角为， ‎ ‎(3) 要使直线平面，只需，‎ 设,则,‎ ‎,‎ ‎，所以,‎ 又 ，由得 解得 所以线段BD上存在点N,使得直线平面AFN，且．‎ ‎6．【山东省安丘市、诸城市、五莲县、兰山区2019届高三5月校级联合考试】如图所示的多面体是由一个直平行六面体被平面所截后得到的，其中，，.‎ ‎（1）求证：平面平面；‎ ‎（2）求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ ‎（1）证明：在中，因为，.‎ 由余弦定理得，，‎ 解得，‎ ‎∴，‎ ‎∴， ‎ 在直平行六面体中，平面，平面，‎ ‎∴‎ 又，‎ ‎∴平面，‎ ‎∴平面平面. ‎ ‎（2）解：如图以为原点建立空间直角坐标系，‎ 因为，，‎ 所以，，，，‎ ‎，，.‎ 设平面的法向量，‎ ‎， ‎ 令，得，，‎ ‎∴. ‎ 设直线和平面的夹角为，‎ 所以，‎ 所以直线与平面所成角的正弦值为.‎ ‎7．【西藏拉萨市2019届高三第三次模拟考试】如图，等边三角形所在平面与梯形所在平面互相垂直，且有，，.‎ ‎（1）证明：平面平面；‎ ‎（2）求二面角的余弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ ‎（1）证明：取中点，连接，‎ 则四边形为菱形，即有，‎ 所以.‎ 又平面，‎ 平面平面，‎ 平面平面，‎ ‎∴平面，‎ 又平面，‎ ‎∴平面平面.‎ ‎（2）由（1）可得，‎ 取中点，连接，则，，‎ 又平面，‎ 平面平面，‎ 平面平面，‎ ‎∴平面.‎ 以为原点建系如图，则 ‎，，，，‎ ‎，，，‎ 设平面的法向量为，则 ‎，取，得.‎ 设平面的法向量为，则，取，，‎ ‎.‎ ‎∴二面角的余弦值为.‎ ‎8．【内蒙古呼伦贝尔市2019届高三模拟统一考试（一)】如图，在直三棱柱中，、、、分别是、、、中点.且，.‎ ‎（1）求证：平面；‎ ‎（2）求二面角的余弦值.‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎（1）∵，，∴.‎ ‎∵是的中点，∴，‎ ‎∵为直三棱柱，，为，中点，‎ ‎∴平面，∴，∴平面.‎ ‎（2）由（1）知建系如图，且，，，，‎ ‎∴，，.‎ 设平面的法向量为，由，得.‎ 取，同理得平面的法向量.‎ ‎∴，而二面角为钝二面角，‎ ‎∴二面角的余弦值为.‎ ‎9．【广东省肇庆市2019届高中毕业班第三次统一检测】如图，在三棱柱中，侧面是菱形，，是棱的中点，，在线段上，且.‎ ‎（1）证明：面；‎ ‎（2）若，面面，求二面角的余弦值．‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ 解：（1）连接交于点，连接．‎ 因为，所以，又因为，所以，所以，‎ 又面，面，所以面.‎ ‎（2）过作于，因为，所以是线段的中点．‎ 因为面面，面面，所以面．连接，‎ 因为是等边三角形，是线段的中点，所以.‎ 如图以为原点，，，分别为轴，轴，轴的正方向建立空间直角坐标，‎ 不妨设，则，，，，，‎ 由，得，的中点，，.‎ 设面的一个法向量为，则，即，‎ 得方程的一组解为，即.‎ 面的一个法向量为，则，‎ 所以二面角的余弦值为.‎ ‎10．【广东省潮州市2019届高三第二次模拟考试】如图，菱形与正三角形的边长均为2，它们所在平面互相垂直，平面，平面．‎ ‎（1）求证：平面平面；‎ ‎（2）若，求二面角的大小．‎ ‎【答案】(1)见证明；(2) ‎ ‎【解析】‎ ‎（1）∵菱形，∴，‎ ‎∵平面，∴，‎ ‎∵，∴平面，‎ ‎∵平面，∴平面平面．‎ ‎（2）设，以为原点，为轴，为轴，‎ 过作平面的垂线为轴，建立空间直角坐标系，‎ 则，，，‎ ‎，，‎ 设平面的法向量，‎ 则，取，得，‎ 平面的法向量，‎ 设二面角的大小为，‎ 则，‎ ‎∴．‎ ‎∴二面角的大小为．‎ ‎11．【山东省栖霞市2019届高三高考模拟卷】如图，在三棱锥中，‎ ‎，侧面底面，，为线段上一点，且满足.‎ ‎（1）若为的中点，求证：；‎ ‎（2）当最小时，求二面角的余弦值.‎ ‎【答案】(1)见证明；(2) ‎ ‎【解析】‎ ‎（1）在，因为,，‎ 为的中点，所以， ‎ 因为面面，面面，所以面，‎ 又面， ‎ ‎（2）以为坐标原点，分别以射线和垂直于面向上的方向为轴，建立空间直角坐标系，‎ 设，则有，因为侧面底面，，‎ 所以， ‎ 所以，‎ 当时，最小，‎ 此时，， ‎ 设为平面的一个法向量，则有，‎ 所以，令，则， ‎ 而平面的一个法向量为，‎ 所以，‎ 故二面角的余弦值为.‎ ‎12．【河南省百校联盟2019届高三考前仿真试卷】如图，在几何体中，四边形为矩形，平面平面，平面，，为棱的中点.‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）求直线与平面所成角的正弦值.‎ ‎【答案】（Ⅰ）证明见解析；（Ⅱ）.‎ ‎【解析】‎ ‎（Ⅰ）因为平面，‎ 所以，‎ 又，‎ 所以平面，‎ 又因为，‎ 所以平面，平面，所以，‎ 因为平面平面，‎ 平面平面，‎ ‎，‎ 所以平面，‎ 经计算可得，‎ 从而，‎ 所以在中，，‎ 又平面，‎ 所以平面.‎ ‎（Ⅱ）如图，以点为原点建立空间直角坐标系，依题意得，‎ ‎.‎ ‎∵，‎ 设平面的一个法向量 则 即消去得，‎ 不妨设，可得，‎ 又，‎ 设直线与平面所成角为，‎ 于是，‎ 故直线与平面所成角的正弦值为.‎ ‎13．【江西省上饶市横峰中学2019届高三考前模拟考试】如图，在三棱锥中，，，为线段上一点，且，平面，与平面所成的角为.‎ ‎（1）求证:平面平面；‎ ‎（2）求二面角的平面角的余弦值。‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ ‎(1)因为，，‎ 所以 所以是直角三角形，；‎ 在中，由，，‎ 不妨设，由得，，，，‎ 在中，由余弦定理得,‎ 故,‎ 所以，所以；‎ 因为平面，平面，‎ 所以，又，‎ 所以平面，又平面，‎ 所以平面平面；‎ ‎(2)因为平面，所以与平面所成的角为，即，‎ 可得为等腰直角三角形，，‎ 由(1)得，以为坐标原点，分别以所在直线为轴，建立如图所示的空间直角坐标系，则，，，，‎ 则为平面的一个法向量。‎ 设为平面的一个法向量，‎ 因为，，‎ 则由得 令，则，，‎ 则为平面的一个法向量，‎ 故 故二面角的平面角的余弦值为.‎ ‎14．【安徽省合肥市2019届高三第三次教学质量检测】已知：在四棱锥中，，，是的中点，是等边三角形，平面平面.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎【答案】（Ⅰ）见证明；（Ⅱ）‎ ‎【解析】‎ 解：（Ⅰ）取的中点为，连结，，，设交于，连结.‎ ‎，‎ 四边形与四边形均为菱形 ‎， ‎ 为等边三角形，为中点 平面平面且平面平面.‎ 平面且 平面 平面 ‎，分别为， 的中点 ‎ 又 ‎ 平面 平面 ‎（Ⅱ）取的中点为，以为空间坐标原点，分别以，，的方向为轴、轴、轴的正方向，建立如图所示的空间直角坐标系.‎ 设，则，，，，.‎ ‎,.‎ 设平面的一法向量.‎ 由 .令，则.‎ 由（Ⅰ）可知，平面的一个法向量.‎ 二面角的平面角的余弦值.‎ ‎15．【湖北部分重点中学2020届高三年级新起点考试】如图四棱锥中，底面是正方形，，且，为中点.‎ ‎（1）求证：平面；‎ ‎（2）求二面角的正弦值.‎ ‎【答案】（1）证明见解析；（2）.‎ ‎【解析】‎ ‎（1）证明：∵底面为正方形，‎ ‎∴，‎ 又，‎ ‎∴平面，‎ ‎∴.‎ 同理，‎ ‎∴平面 .‎ ‎（2）建立如图的空间直角坐标系，不妨设正方形的边长为2‎ 则，设为平面的一个法向量，‎ 又， ‎ ‎，令，得.‎ 同理是平面的一个法向量， ‎ 则.‎ ‎∴二面角的正弦值为.‎ ‎16．【江西省鹰潭市2019届高三第一次模拟】如图，在四棱锥中，平面，，，，，是的中点．‎ ‎ ‎ ‎（1）求和平面所成的角的大小．‎ ‎（2）求二面角的正弦值．‎ ‎【答案】（1）（2）‎ ‎【解析】‎ 解：（1）在四棱锥中，∵平面，平面，‎ ‎∴．又，，∴平面．‎ 故在平面内的射影为，从而为和平面所成的角．‎ 在中，，故．‎ 所以和平面所成的角的大小为．‎ ‎（2）在四棱锥中，∵平面，平面，∴．‎ 由条件，，∴平面．‎ 又∵平面，∴．由，，可得．‎ ‎∵是的中点，∴．又∵，∴平面．‎ 过点作，垂足为，连接，如图所示．‎ ‎∵平面，在平面内的射影是，‎ ‎∴．∴是二面角的平面角．‎ 由已知∵，∴设，‎ 则，，，．‎ 中，．‎ 在中，∵，∴，得．‎ 在中，．‎ 所以二面角的正弦值为．‎ ‎17．【山东省实验中学等四校2019届高三联合考试】如图在直角中，为直角，，，分别为，的中点，将沿折起，使点到达点的位置，连接，，为的中点．‎ ‎（Ⅰ）证明：面；‎ ‎（Ⅱ）若，求二面角的余弦值．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎【解析】‎ 证明：（Ⅰ ）取中点，连结、，‎ ‎∵ ，，‎ ‎∴ 四边形是平行四边形，‎ ‎∵ ，，，‎ ‎∴ ，‎ ‎∴ ，∴，‎ 在中，，‎ 又∵ 为的中点，∴，‎ 又∵ ，∴．‎ 解：（Ⅱ）∵，，，‎ ‎∴ ，‎ 以为原点，、、所在直线分别为，，轴，建立空间直角坐标系，‎ 设，则，，，，‎ ‎∴ ，，，‎ 设面的法向量，‎ 则，取，得，‎ 同理，得平面的法向量，‎ 设二面角的平面角为，‎ 则，‎ ‎∴ 二面角的余弦值为．‎ ‎18．【北京市房山区2019年第二次高考模拟检测高三】已知四棱锥，底面为菱形，,为上的点，过的平面分别交，于点，，且平面．‎ ‎（1）证明：；‎ ‎（2）当为的中点，，与平面所成的角为，求与平面所成角的正弦值．‎ ‎【答案】(1)见证明(2) ‎ ‎【解析】‎ ‎（1）‎ 连结、且，连结．‎ 因为，为菱形，所以，，‎ 因为，，所以，，‎ 因为，且、平面，‎ 所以，平面，‎ 因为，平面，所以，，‎ 因为，平面，‎ 且平面平面，‎ 所以，， ‎ 所以，．‎ ‎（2）‎ 由（1）知且，‎ 因为，且为的中点，‎ 所以，，所以，平面,‎ 所以与平面所成的角为，所以，‎ 所以，，，因为，，所以，.‎ 以，，分别为，，轴，如图所示建立空间直角坐标系 记，所以，，，，，，，，‎ 所以， ，，‎ 记平面的法向量为，所以，即，‎ 令，解得，，所以，，‎ 记与平面所成角为，所以，.‎ 所以，与平面所成角的正弦值为.‎ ‎19．【北京市房山区2019年第二次高考模拟检测高三】已知正方形和矩形所在的平面互相垂直，，点在线段上.‎ ‎（Ⅰ）若为的中点，求证：平面；‎ ‎（Ⅱ）求二面角的余弦值；‎ ‎（Ⅲ）证明：存在点，使得平面，并求的值.‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）；（Ⅲ）详见解析.‎ ‎【解析】‎ ‎（Ⅰ）设，连结，‎ 因为正方形，所以为中点 又矩形,为的中点 所以且 所以为平行四边形 所以 又平面，平面 所以平面 ‎（Ⅱ）以为原点，分别以为轴建立坐标系 则 设平面的法向量为，‎ 由得 则 易知平面的法向量 由图可知二面角为锐角 所以二面角的余弦值为 ‎（Ⅲ）设，则 若平面，则，即 所以解得所以 所以 ‎20．【甘肃省兰州市第一中学2019届高三6月最后高考冲刺模拟】如图，在直三棱柱中，平面侧面，且，‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）若直线与平面所成角的大小为，求锐二面角的大小．‎ ‎【答案】（Ⅰ）详见解析；（Ⅱ）.‎ ‎【解析】‎ ‎（Ⅰ）如图，取的中点，连接.‎ 因为，所以.‎ 由平面侧面，且平面侧面，‎ 得平面.‎ 又平面，所以，‎ 因为三棱柱是直三棱柱，则底面，所以 ‎ 又，从而侧面，‎ 又侧面，故． ‎ ‎(Ⅱ)由（1）知且底面，所以以点为原点，以所在直线分别为， ，轴建立空间直角坐标系.‎ 设，则，，，，，，，.‎ 设平面的一个法向量，由，，得.‎ 令，得，则.‎ 设直线与平面所成的角为，则，‎ 所以，‎ 解得， 即.‎ 又设平面的一个法向量为，同理可得.‎ 设锐二面角的大小为，则，‎ 由，得.‎ ‎∴锐二面角的大小为.‎ 能力提升训练 1．【北京市通州区2019届高三4月第一次模拟】如图1，菱形中，，， 于．将沿翻折到，使，如图2．‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求直线A′E与平面A′BC所成角的正弦值；‎ ‎（Ⅲ）设为线段上一点，若平面，求的值．‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）；（Ⅲ）1‎ ‎【解析】‎ ‎（Ⅰ）在菱形中，因为，所以，．‎ 所以．因为，，平面，平面，‎ 所以平面．因为平面，‎ 所以平面⊥平面．‎ ‎（Ⅱ）由（Ⅰ）知，，，如图建立空间直角坐标系，‎ 则 ，，,, ，‎ 所以，,．‎ 设平面的法向量，由 得所以令，则.所以．‎ 所以，又 ,，‎ 所以.‎ 所以直线与平面所成角的正弦值为．‎ ‎（Ⅲ）由（Ⅱ）可知，,‎ 设，则．‎ 因为 平面，所以，即．‎ 所以，即．所以．‎ ‎ 2．【辽宁省丹东市2019届高三总复习质量测试】如图，四棱锥中，平面，，，，，，是中点，是线段上的点.‎ ‎（1）若是中点，求证：平面；‎ ‎（2）设与平面所成角为，求最大值.‎ ‎【答案】（1）见证明；（2）‎ ‎【解析】‎ 解法1：（1）以为坐标原点，射线为轴的正半轴，建立如图所示的直角坐标系，设.‎ 则，，，，，所以，，.‎ 因为平面，所以，又，所以平面，平面一个法向量为.‎ 因为，平面，所以平面.‎ ‎（2），设，则，.‎ 平面的一个法向量为，所以.‎ 因为，所以当，即时，取得最大值.‎ 解法2：‎ ‎（1）取中点为，连结，，则，因为平面，所以平面，同理平面.所以平面平面，因此平面.‎ ‎（2）以为坐标原点，射线为轴的正半轴，建立如图所示的直角坐标系，设，‎ 则，，，，，所以，，.‎ 设，则，.‎ 平面的一个法向量为，所以.‎ 因为，所以当，即时，取得最大值.‎ 解法3：‎ ‎（1）同解法2.‎ ‎（2）因为，所以.‎ 因为平面，所以，.所以平面，则.‎ 设，则，，.‎ 的最小值为到距离等于，所以的最大值. ‎ ‎3．【河南省郑州市2019届高三第三次质量检测】如图，，，，，分别为，边的中点，以为折痕把折起，使点到达点的位置，且..‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）设为线段上动点，求直线与平面所成角的正弦值的最大值.‎ ‎【答案】（Ⅰ）见解析；‎ ‎（Ⅱ）.‎ ‎【解析】‎ ‎（Ⅰ）E,F分别为AB ,AC边的中点,所以 因为 ‎ 又因为 ，所以平面．‎ ‎（Ⅱ）取BE的中点O,连接PO, ‎ 由（1）知平面,EF平面BCFE，,‎ 所以平面PBE平面BCFE 因为PB=BE=PE,所以PO,‎ 又因为PO平面PBE,平面PBE平面BCFE=BE 所以PO . ‎ 过O作OM//BC交CF于M,分别以OB，OM，OP所在直线为 x,y,z轴建立空间直角坐标系,如图所示.‎ ‎ ‎ N为线段PF上一动点设,由,‎ 得 设平面PCF的法向量为 则 即取 ‎ 设直线BN与平面PCF所成角 ‎ 直线BN与平面PCF所成角的正弦值的最大值为 4．【安徽省江淮十校2019届高三年级5月考前最后一卷】在三棱柱中平面平面，，是棱的中点.‎ ‎（1）求证：平面平面；‎ ‎（2）若，求二面角的余弦值.‎ ‎【答案】(1)见解析；(2) .‎ ‎【解析】‎ ‎（1）取的中点,连接与交于点，连接，,‎ 则 为的中点， ,且，所以是平行四边形.‎ 又是棱的中点，所以 . ‎ 侧面底面，，且 ，，‎ 所以平面 ，得平面，又平面，‎ 所以平面平面.‎ ‎（2）连接，因为，所以是等边三角形，设.‎ 故 面 ，由已知可得 .以 分别为轴建立空间直角坐标系.‎ 则 ， ，‎ 设平面的法向量为 则，‎ 所以 ，取 ，所以 ‎ 设平面的法向量为 ‎ , ‎ 则，所以，取 ，‎ 故 ，因为二面角为锐角，所以其余弦值为. ‎ ‎ 5．【山西省2019届高三高考考前适应性训练（三)】在三棱柱中，，侧面底面，D是棱的中点.‎ ‎（1）求证：平面平面；‎ ‎（2）若，求二面角的余弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ 解：（1）取的中点，连接与交于点，连接.‎ 则为的中点，‎ 因为三棱柱，‎ 所以，且，‎ 所以四边形是平行四边形.‎ 又是棱的中点，所以.‎ 因为侧面底面，且，‎ 所以平面 所以平面 又平面，‎ 所以平面平面 ‎（2）连接，因为，所以是等边三角形，故底面。‎ 设，可得，‎ 分别以分别为轴正方向建立空间直角坐标系，‎ 则 设平面的一个法向量为 则 所以，取 所以 又平面的一个法向量为 故 因为二面角为钝角，所以其余弦值为. 6．【江西省名校（临川一中、南昌二中)2019届高三5月联合考试】已知空间几何体中，与均为边长为的等边三角形，为腰长为的等腰三角形，平面平面，平面平面.‎ ‎（1）试在平面内作一条直线，使直线上任意一点与的连线均与平面平行，并给出详细证明；‎ ‎（2）求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ 如图所示:取BC和BD的中点H、G，连接HG.HG为所求直线.‎ 所以,‎ 因为平面平面，,‎ 所以，‎ 取CD中点O,连接EO,‎ 因为平面平面，‎ 所以，‎ 所以AH||EO,又平面CDE,平面CDE,‎ 所以.‎ 因为,‎ 所以,‎ 因为,‎ 则，‎ 所以直线HG上任意一点与的连线均与平面平行.‎ ‎(2)以CD中点O为坐标原点，OD所在直线为x轴，OB所在直线为Y轴，OE所在直线为Z轴,建立空间直角坐标系.,‎ 设 所以.‎ 所以直线与平面所成角的正弦值为.‎ ‎ 7．【北京市昌平区2019届高三5月二模】如图，在四棱锥中，底面为矩形，平面平面,,，，为中点．‎ ‎（Ⅰ）求证：∥平面； ‎ ‎（Ⅱ）求二面角的余弦值；‎ ‎（Ⅲ）在棱上是否存在点，使得？若存在，求的值；若不存在，说明理由．‎ ‎【答案】（I）见解析； （II）； （Ⅲ）答案见解析 .‎ ‎【解析】‎ ‎（I）设交于点，连结.‎ 因为底面是矩形,所以为中点 .‎ 又因为为中点 , 所以∥.‎ 因为平面平面,所以∥平面. ‎ ‎（II）取的中点，连结，.‎ 因为底面为矩形,所以.‎ 因为，,‎ 所以∥，所以.‎ 又因为平面PCD⊥平面ABCD,平面平面PCD∩平面ABCD=CD.‎ 所以PO⊥平面ABCD，‎ 如图，建立空间直角坐标系,则，‎ 设平面的法向量为， ‎ 所以 令，则，所以.‎ 平面的法向量为，则.‎ 如图可知二面角为钝角，所以二面角的余弦值为.‎ ‎（Ⅲ）在棱上存在点, 使.‎ 设,则.　‎ 因为,所以.‎ ‎.‎ 因为,所以.‎ 所以，解得.‎ 所以在棱上存在点,使，且. 8．【北京市朝阳区2019届高三第二次（5月)综合练习】在三棱柱中，底面是正三角形，侧棱底面．D，E分别是边BC，AC的中点，线段与交于点G，且，．‎ ‎（1）求证：∥平面；‎ ‎（2）求证：⊥平面；‎ ‎（3）求二面角的余弦值．‎ ‎【答案】（1）见解析；（2）见解析；（3）.‎ ‎【解析】‎ ‎（1）证明：因为E为AC中点，G为B‎1C中点．所以EG∥AB1．‎ 又因为EG⊄平面AB1D，AB1⊂平面AB1D，‎ 所以EG∥平面AB1D． ‎ ‎（2） 证明：取B‎1C1的中点D1，连接DD1．‎ 显然DA，DC，DD1两两互相垂直，如图，建立空间直角坐标系D-xyz，‎ 则D（0，0，0），，B（0，-2，0），，，，C ‎（0，2，0）．‎ 所以，，．‎ 又因为，，‎ 所以BC1⊥DA，BC1⊥DB1．‎ 又因为DA∩DB1=D，所以BC1⊥平面AB1D． ‎ ‎（3）解：显然平面B1CB的一个法向量为=（1，0，0）．‎ 设平面AB‎1C的一个法向量为：=（x，y，z），‎ 又，，‎ 由得 设x=1，则，，则．‎ 所以．‎ 设二面角A-B‎1C-B的平面角为θ，由图可知此二面角为锐二面角，‎ 所以． 9．【重庆南开中学2019届高三第四次教学检测】在直角梯形中，，，，，分别为，的中点（如图1）．沿将四边形折起，使得（如图2）．‎ ‎ ‎ ‎（1）求证：平面平面；‎ ‎（2）若，求二面角的余弦值．‎ ‎【答案】(1)见证明；(2) ‎ ‎【解析】‎ ‎（1）由题设条件，，则，又且 则平面，又平面 故平面平面 ‎（2）如图，建立空间角坐标系，则， ，‎ 设，则有，，‎ 由知 解得 ‎ 从而，，， ‎ 平面的法向量为 ‎ 设平面的法向量为 ‎ 由得取y=,得 则二面角的余弦值为 10．【山东省泰安市教科研中心2019届高三考前密卷】如图，在直三棱柱ABC﹣A1B‎1C1（侧棱垂直于底面的棱柱）中，CA⊥CB，CA＝CB＝CC1＝2，动点D在线段AB上．‎ ‎（1）求证：当点D为AB的中点时，平面B1CD⊥上平面ABB‎1A1；‎ ‎（2）当AB＝3AD时，求平面B1CD与平面BB‎1C1C所成的锐二面角的余弦值．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎（1）∵在等腰Rt△ABC中，D为斜边AB的中点，∴CD⊥AB，‎ 又∵在直三棱柱ABC﹣A1B‎1C1中，B1B⊥平面ABC，CD⊂平面ABC，‎ ‎∴B1B⊥CD，∵AB∩B1B＝B，∴CD⊥平面ABB‎1A1，‎ 又CD⊂平面B1CD，∴平面B1CD⊥上平面ABB‎1A1．‎ ‎（2）如图，∵CA，CB，CC1两两垂直，‎ ‎∴以C为原点，CA，CB，CC1所在直线分别为x，y，z轴，建立空间直角坐标系，‎ 则C（0，0，0），A（2，0，0），B（0，2，0），B1（0，2，2），D，‎ ‎（0，2，2），，‎ 设平面B1CD的法向量＝（x，y，z），则，令z＝1，得，‎ 平面BB‎1C1C的法向量＝（2，0，0），‎ 设平面B1CD与平面BB‎1C1C所成的锐二面角的平面角为θ，‎ 则cosθ＝ ，‎ ‎∴平面B1CD与平面BB‎1C1C所成的锐二面角的余弦值为．‎