高中数学第二讲参数方程二圆锥曲线的参数方程课堂探究学案新人教A版选修4-41 3页

二 圆锥曲线的参数方程 课堂探究 探究一 椭圆的参数方程的应用 在求解一些最值问题时，可以用参数方程来表示曲线上点的坐标，利用正弦、余弦函数 的有界性来解决问题，简化运算过程．另外，利用椭圆的参数方程可以解决一些与椭圆有关 的特殊动点的轨迹问题． 【例题 1】在椭圆x2 25 ＋y2 16 ＝1 中有内接矩形，问内接矩形的最大面积是多少？ 解：椭圆的参数方程为 x＝5cos t， y＝4sin t (t 为参数)． 设第一象限内椭圆上一点 M(x，y)，由椭圆的对称性，知内接矩形面积为 S＝4xy＝4×5cos t×4sin t＝40sin 2t. 当 t＝π 4 时，面积 S 取得最大值 40，此时 x＝5cosπ 4 ＝5 2 2 ，y＝4sinπ 4 ＝2 2. 因此，矩形在第一象限的顶点为 5 2 2 ，2 2 ，此时内接矩形的面积最大，且为 40. 探究二 双曲线的参数方程的应用 1．利用双曲线的参数方程可进行三角代换，从而将有关问题转化为三角函数问题求解． 2．直线与双曲线位置关系的综合题，可考虑利用双曲线的参数方程设元，再探求解题 方法． 【例题 2】如图，设 P 为等轴双曲线 x2－y2＝1 上的一点，F1，F2 是两个焦点，证明： |PF1|·|PF2|＝|OP|2. 思路分析：设 P 1 cos φ ，tan φ ，证明等式两边等于同一个式子即可． 证明：设 P 1 cos φ ，tan φ ， ∵F1(－ 2，0)，F2( 2，0)， ∴|PF1|＝ 1 cos φ ＋ 2 2＋tan2φ ＝ 2 cos2φ ＋ 2 2 cos φ ＋1， |PF2|＝ 1 cos φ － 2 2＋tan2φ ＝ 2 cos2φ － 2 2 cos φ ＋1. ∴|PF1|·|PF2| ＝ 2 cos2φ ＋1 2－ 8 cos2φ ＝ 2 cos2φ －1. ∵|OP|2＝ 1 cos2φ ＋tan2φ＝ 2 cos2φ －1， ∴|PF1|·|PF2|＝|OP|2. 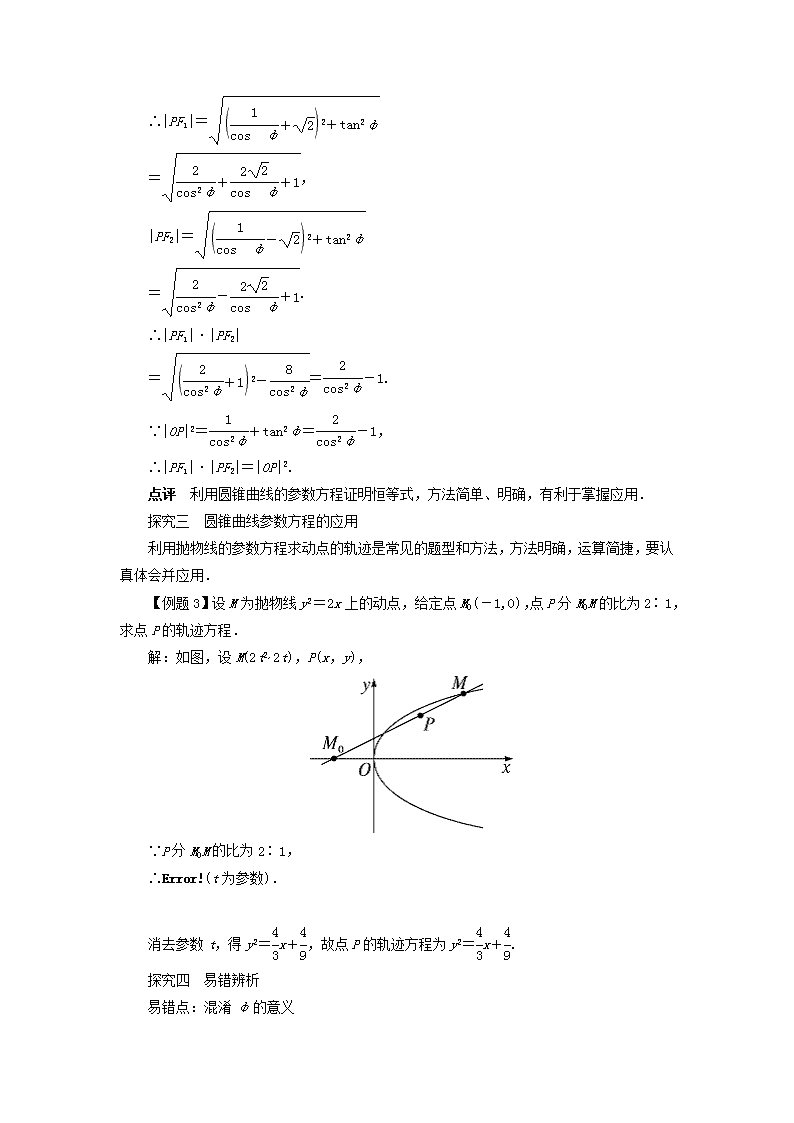点评 利用圆锥曲线的参数方程证明恒等式，方法简单、明确，有利于掌握应用． 探究三 圆锥曲线参数方程的应用 利用抛物线的参数方程求动点的轨迹是常见的题型和方法，方法明确，运算简捷，要认 真体会并应用． 【例题 3】设 M 为抛物线 y2＝2x 上的动点，给定点 M0(－1,0)，点 P 分 M0M 的比为 2∶1， 求点 P 的轨迹方程． 解：如图，设 M(2t2,2t)，P(x，y)， ∵P 分 M0M 的比为 2∶1， ∴ x＝－1＋2×2t2 1＋2 ＝－1＋4t2 3 ， y＝0＋2×2t 1＋2 ＝4t 3 (t 为参数)． 消去参数 t，得 y2＝4 3 x＋4 9 ，故点 P 的轨迹方程为 y2＝4 3 x＋4 9 . 探究四 易错辨析 易错点：混淆φ的意义 【例题 4】已知 P 为椭圆x2 16 ＋y2 12 ＝1 上一点，且∠POx＝π 3 ，求点 P 的坐标． 错解：设点 P 的坐标为(x，y)，如图所示，由椭圆的参数方程得 x＝4cosπ 3 ， y＝2 3sinπ 3 ， 即 P 的坐标为(2,3)． 错因分析：椭圆 x＝acos φ， y＝bsin φ (φ为参数)和圆 x＝rcos φ， y＝rsin φ (φ为参数)中，参 数φ的意义是不同的．在圆的方程中，φ是圆周上的动点 M(x，y)所对应的角∠xOM，而椭 圆方程中的φ，其意义却不是这样，上述解答把椭圆方程中φ的意义错混为圆的方程中φ的 意义，从而导致了解答的错误． 正解：设|OP|＝t，点 P 的坐标为 tcosπ 3 ，tsinπ 3 ，代入椭圆方程得 1 2 t 2 16 ＋ 3 2 t 2 12 ＝1， 即 t＝8 5 5 ，所以点 P 的坐标为 4 5 5 ，4 15 5 .