- 68.09 KB
- 2021-06-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
16.5二项式定理(1)
教学目标 初步掌握二项式定理及相关概念、公式。
教学重点与难点
二项式定理。 二项式定理的理解。
教学方法 温故知新,启发式讲授法,讲练结合法。
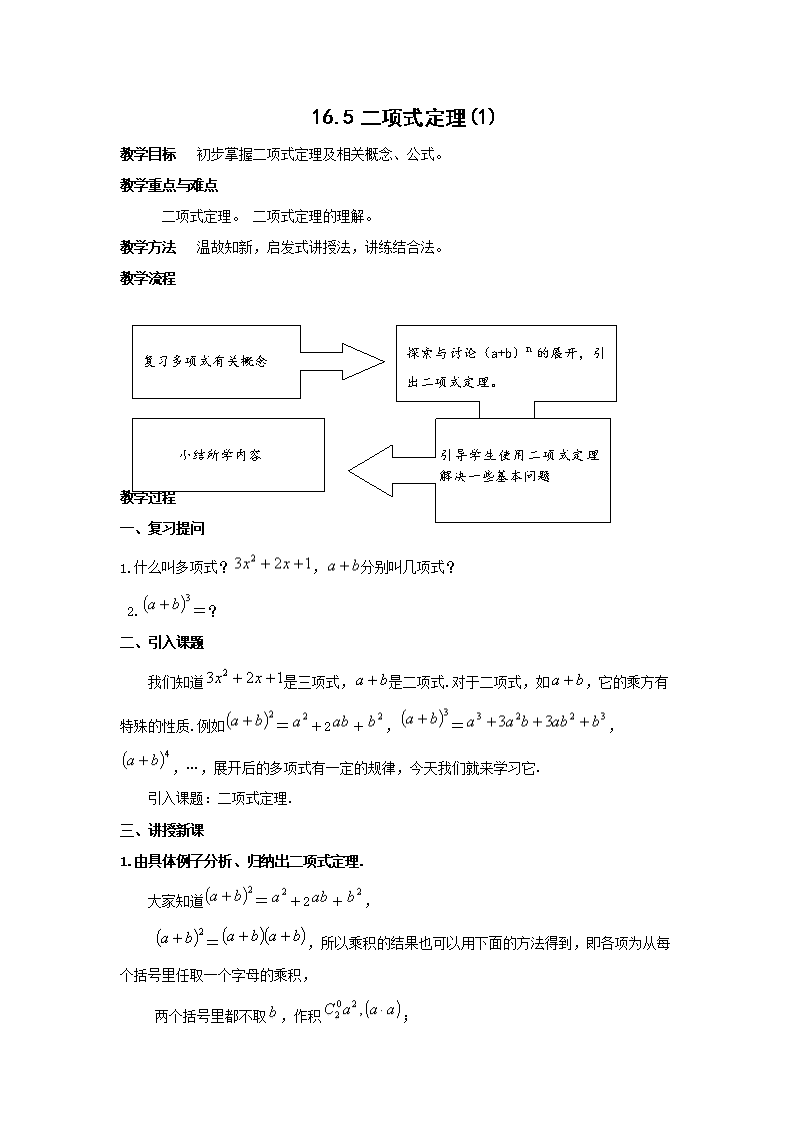
教学流程
探索与讨论(a+b)n的展开,引出二项式定理。
复习多项式有关概念
引导学生使用二项式定理解决一些基本问题
小结所学内容
教学过程
一、复习提问
1.什么叫多项式?,分别叫几项式?
2.=?
二、引入课题
我们知道是三项式,是二项式.对于二项式,如,它的乘方有特殊的性质.例如=+2+,=,,…,展开后的多项式有一定的规律,今天我们就来学习它.
引入课题:二项式定理.
三、讲授新课
1.由具体例子分析、归纳出二项式定理.
大家知道=+2+,
=,所以乘积的结果也可以用下面的方法得到,即各项为从每个括号里任取一个字母的乘积,
两个括号里都不取,作积;
在两个括号里有一个取,作积;
两个括号里都取,作积.
因此,.
再看= (),它的等号右边的积的展开式的每一项,是从每一个括号里任取一个字母的乘积,因而各项都是3次式,即展开式应有下面形式的各项: ,,,.在上面3个括号中:每个都不取的情况有1种,记为种,所以的系数是;恰有1个取的情况有种,所以的系数是;恰有2个取的情况有种,所以的系数是;3个都取的情况有1种,记为种,所以的系数是.
因此,
.
同样,,
一般地,对于任意正整数,上面的关系式也是成立的,即
这个公式所表示的定理叫做二项式定理,右边的多项式叫做的二项展开式,它一共有项,其中各项的系数叫做二项式系数.式子中的叫做二项展开式的通项,用表示,即通项为展开式的第项:
.
在二项式定理中,如果设=1,=,则得到公式(公式可以直接利用):
2.例题
例1 求的二项展开式.
分析:这里,直接代公式.
解:
例2 求的二项展开式的第6项.
解:
.
例3 求的二项展开式中的系数.
分析:用设未知数列方程的思想.
解:设第项含,则有
根据题意,得
,
解得=3. 因此,的系数是.
例4 求的展开式的第4项的系数.
分析:的展开式第4项的二项式系数是,这里是求第4项的系数,而不是二项式第4项的系数,不能弄混.
解:
所以展开式第4项的系数是280.
例5 计算的近似值(精确到0.001).
解: = =1-5×0.003+10×-…
根据题中精确度的要求,从第3项以后各项都可勿略不计,所以
≈1-5×0.003=0.985.
四、课堂小结
(1)二项式定理:
.
(2)二项展开式的通项(注意:它是第项).
(3)二项式系数: 等组合数.
二项展开式某一项的系数是指该项的数字因数或相当数字因数.
相关文档
- 高中数学第二讲参数方程二圆锥曲线2021-06-153页
- 【数学】2019届一轮复习北师大版正2021-06-1512页
- 高中数学分章节训练试题:17等差数列2021-06-154页
- 高中数学一轮复习文数通用版:选修4-2021-06-1543页
- 2020年高中数学新教材同步必修第一2021-06-1528页
- 2012高中数学 1_4_1、2课时同步练2021-06-153页
- 人教A高中数学必修三程序框图与算2021-06-156页
- 浙江省2021届高考数学一轮复习第六2021-06-1533页
- 2019-2020学年高中数学第二章参数2021-06-1525页
- 高中数学人教a版必修二 章末综合测2021-06-159页