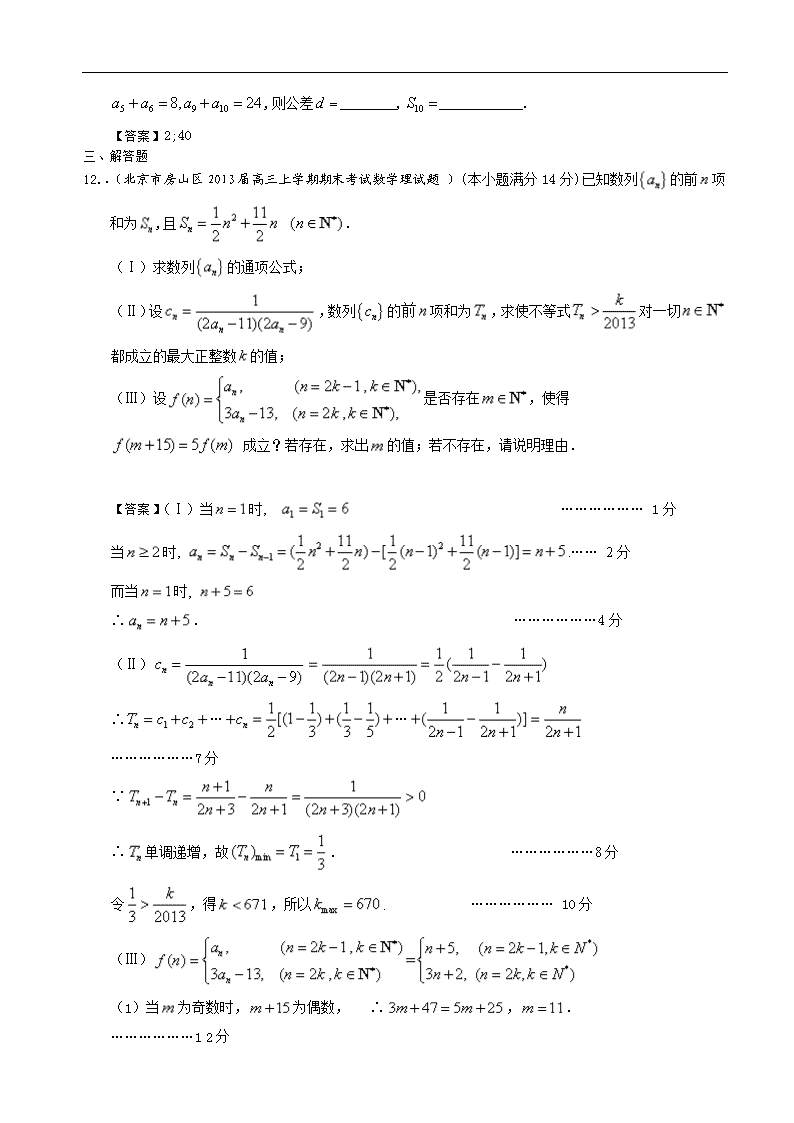2014届高三理科数学一轮复习试题选编12：等差数列（教师版） 7页

‎2014届高三理科数学一轮复习试题选编12：等差数列 一、选择题 ．（北京市东城区2013届高三上学期期末考试数学理科试题）已知为等差数列，其前项和为，若，，则公差等于 （　　）‎ A． B． C． D．‎ ‎【答案】C 解：因为，，所以，解得，所使用，解得，选 C．‎ ．（2013届北京市高考压轴卷理科数学）为等差数列,为其前项和, 则 （　　）‎ A． B． C． D．‎ ‎【答案】A ‎ ‎【解析】设公差为,则由得,即,解得,所以,所以.所以,选A． ‎ ．（北京市海淀区北师特学校2013届高三第四次月考理科数学）已知正项数列中，，，，则等于 （　　）‎ A．16 B．‎8 ‎C． D．4‎ ‎【答案】D ‎【解析】由可知数列是等差数列，且以为首项，公差，所以数列的通项公式为，所以，即。选 D．‎ ．（北京市昌平区2013届高三上学期期末考试数学理试题 ）设是公差不为0的等差数列的前项和，且成等比数列，则等于 （　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【答案】C 解：因为成等比数列，所以，即，即，所以，选 C．‎ ．（北京市东城区普通高中示范校2013届高三12月综合练习(一)数学理试题）在等差数列中,,且,则的最大值是 （　　）‎ A． B． C． D．‎ ‎【答案】C【解析】在等差数列中,,得,即,由,所以,即,当且仅当时取等号,所以的最大值为9,选 C． ‎ 二、填空题 ．（2013北京西城高三二模数学理科）在等差数列中,,,则______;设,则数列的前项和______. ‎ ‎【答案】 ,; ‎ ．（2013届北京海滨一模理科）等差数列中,, 则 ‎【答案】14 ‎ ．（2012北京理）已知等差数列为其前n项和.若,,则=_______.‎ ‎【答案】【解析】因为,‎ 所以,.‎ ‎【答案】,‎ ．（2013届北京西城区一模理科）设等差数列的公差不为，其前项和是．若，，则______．‎ ‎【答案】； ‎ ．（北京市石景山区2013届高三一模数学理试题）在等差数列{an}中,al=-2013,其前n项和为Sn,若=2,则的值等于___________.‎ ‎【答案】 ‎ ．（北京市朝阳区2013届高三上学期期中考试数学（理）试题）设是等差数列的前项和.若 ‎,则公差________,____________.‎ ‎【答案】2;40 ‎ 三、解答题 ．（北京市房山区2013届高三上学期期末考试数学理试题 ）(本小题满分14分)已知数列的前项和为,且 .‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设，数列的前项和为，求使不等式对一切都成立的最大正整数的值；‎ ‎（Ⅲ）设是否存在，使得 ‎ 成立？若存在，求出的值；若不存在，请说明理由．‎ ‎【答案】（Ⅰ）当时, ……………… 1分 当时, .…… 2分 而当时, ‎ ‎∴． ………………4分 ‎（Ⅱ） ‎ ‎∴……‎ ‎………………7分 ‎∵‎ ‎∴单调递增，故． ………………8分 令，得，所以. ……………… 10分 ‎（Ⅲ）‎ ‎（1）当为奇数时，为偶数， ∴，．‎ ‎………………1 2分 ‎（2）当为偶数时，为奇数， ∴，（舍去）．‎ 综上，存在唯一正整数，使得成立．‎ ‎……………………1 4分 ．（北京市海淀区2013届高三上学期期中练习数学（理）试题）已知等差数列的前项和为,且,.‎ ‎(Ⅰ)求数列的通项公式;‎ ‎(Ⅱ)求使不等式成立的的最小值.‎ ‎【答案】解:(I)设的公差为, ‎ 依题意,有 ‎ 联立得 ‎ 解得 ‎ 所以 ‎ ‎(II)因为,所以 ‎ 令,即 ‎ 解得或 ‎ 又,所以 ‎ 所以的最小值为 ‎ ．（北京市海淀区北师特学校2013届高三第四次月考理科数学）数列{}中，，，且满足 ‎(1)求数列的通项公式；‎ ‎(2)设，求．‎ ‎【答案】解：(1)∴‎ ‎∴为常数列，∴{an}是以为首项的等差数列，‎ 设，,∴，∴．‎ ‎(2)∵，令，得．‎ 当时，；当时，；当时，．‎ ‎∴当时，‎ ‎，．‎ 当时，．‎ ‎∴‎ ．（北京四中2013届高三上学期期中测验数学(理)试题）设等差数列的首项及公差d都为整数,前n项和为Sn.‎ ‎(1)若,求数列的通项公式;‎ ‎(2)若 求所有可能的数列的通项公式.‎ ‎【答案】解: ‎ ‎(Ⅰ)由 ‎ 又 ‎ 故解得 ‎ 因此,的通项公式是1,2,3,, ‎ ‎(Ⅱ)由 得 ‎ 即 ‎ 由①+②得-7d<11,即 ‎ 由①+③得, 即, ‎ 于是 又,故. ‎ 将4代入①②得 ‎ 又,故 ‎ 所以,所有可能的数列的通项公式是 ‎ ‎1,2,3,. ‎ ．（北京市东城区普通高中示范校2013届高三3月联考综合练习（二）数学（理）试题 ）已知数集具有性质：对，与两数中至少有一个属于．‎ ‎(1) 分别判断数集与数集是否具有性质，说明理由；‎ ‎(2) 求证：；‎ ‎(3) 已知数集具有性质．证明：数列是等差数列．‎ ‎【答案】解：由于和都不属于集合，所以该集合不具有性质；由于、、、、、、、、、都属于集合，所以该数集具有性质． …………………………………………4分 (1) 具有性质，所以与中至少有一个属于 由，有，故 ‎，故 ‎，故 由具有性质知，‎ 又，‎ ‎，，…，，‎ 从而 故 ……………………8分 由(2)可知，‎ ‎…………………………①‎ 由知，，，…，，均不属于 由具有性质，，，…，，均属于 ‎，，，…，‎ 即…………………………②‎ 由①②可知 故构成等差数列． …………………………………13分