2020高考数学二轮复习练习：第一部分 小题分类练 小题分类练（四） 图表信息类含解析 9页

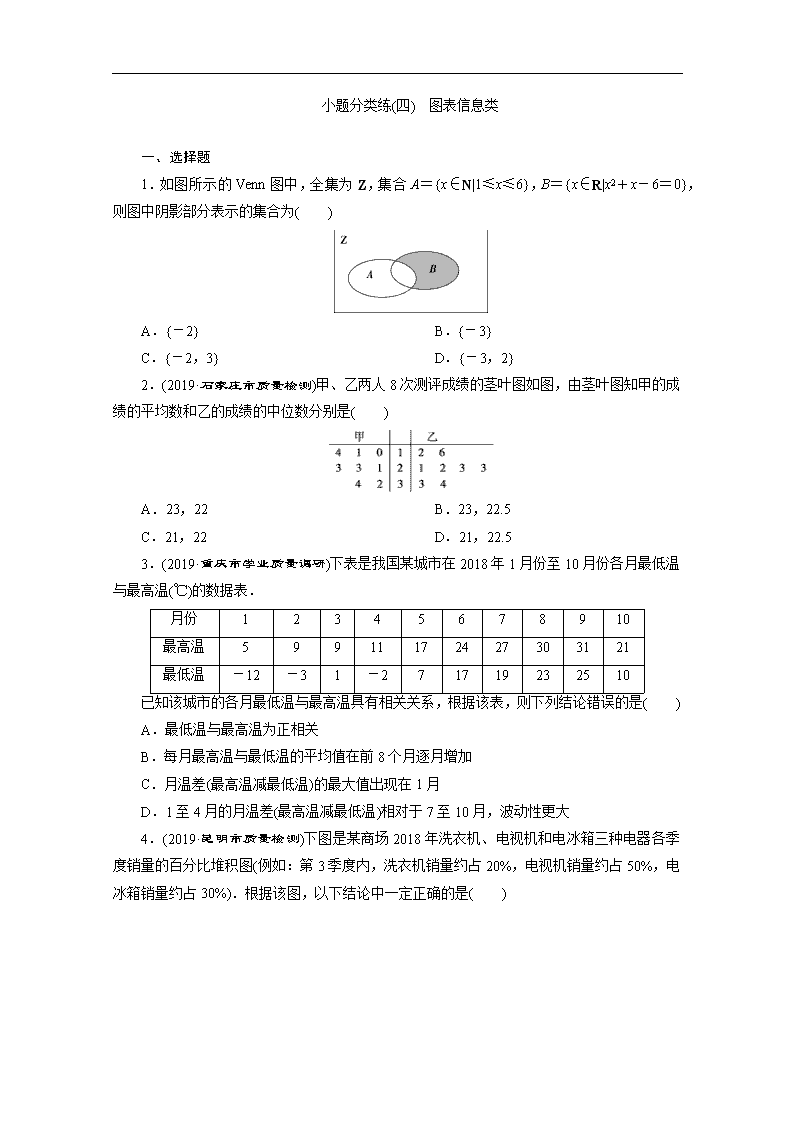
小题分类练(四)　图表信息类 一、选择题 ‎1．如图所示的Venn图中，全集为Z，集合A＝{x∈N|1≤x≤6}，B＝{x∈R|x2＋x－6＝0}，则图中阴影部分表示的集合为(　　)‎ A．{－2} B．{－3}‎ C．{－2，3} D．{－3，2}‎ ‎2．(2019·石家庄市质量检测)甲、乙两人8次测评成绩的茎叶图如图，由茎叶图知甲的成绩的平均数和乙的成绩的中位数分别是(　　)‎ A．23，22 B．23，22.5 ‎ C．21，22 D．21，22.5‎ ‎3．(2019·重庆市学业质量调研)下表是我国某城市在2018年1月份至10月份各月最低温与最高温(℃)的数据表．‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 最高温 ‎5‎ ‎9‎ ‎9‎ ‎11‎ ‎17‎ ‎24‎ ‎27‎ ‎30‎ ‎31‎ ‎21‎ 最低温 ‎－12‎ ‎－3‎ ‎1‎ ‎－2‎ ‎7‎ ‎17‎ ‎19‎ ‎23‎ ‎25‎ ‎10‎ 已知该城市的各月最低温与最高温具有相关关系，根据该表，则下列结论错误的是(　　)‎ A．最低温与最高温为正相关 B．每月最高温与最低温的平均值在前8个月逐月增加 C．月温差(最高温减最低温)的最大值出现在1月 D．1至4月的月温差(最高温减最低温)相对于7至10月，波动性更大 ‎4．(2019·昆明市质量检测)下图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如：第3季度内，洗衣机销量约占20%，电视机销量约占50%，电冰箱销量约占30%)．根据该图，以下结论中一定正确的是(　　)‎ A．电视机销量最大的是第4季度 B．电冰箱销量最小的是第4季度 C．电视机的全年销量最大 D．电冰箱的全年销量最大 ‎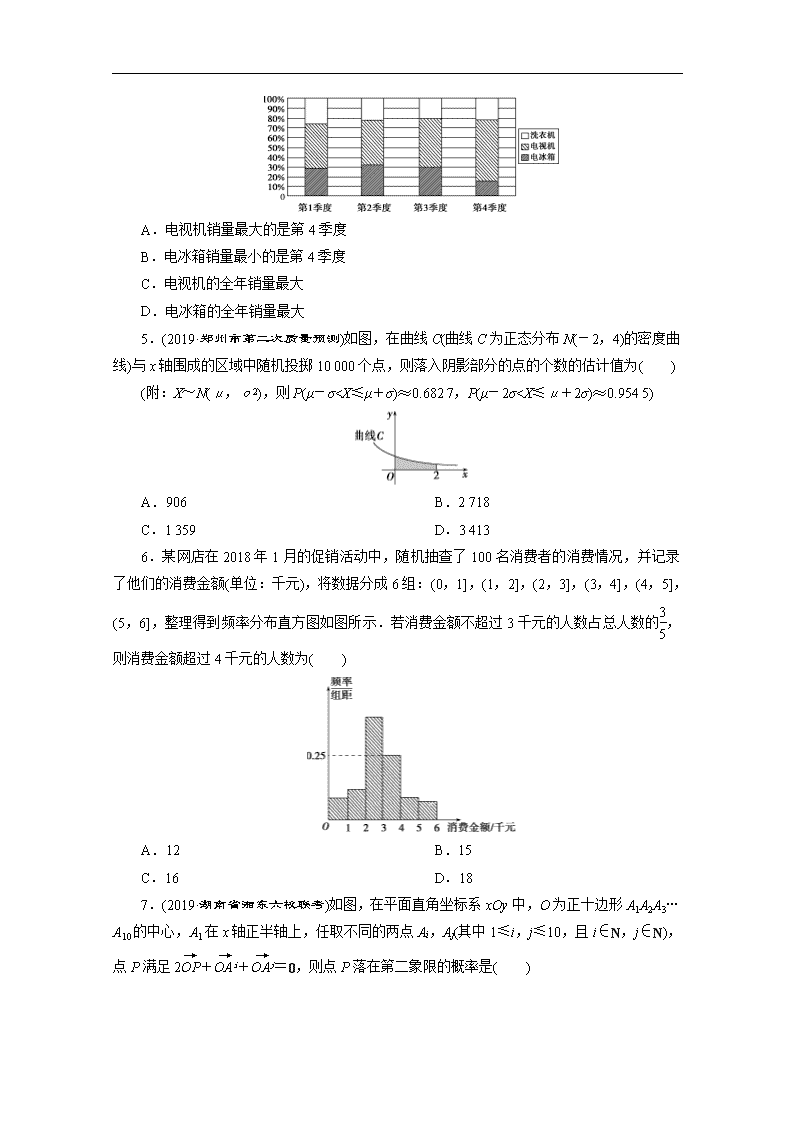5．(2019·郑州市第二次质量预测)如图，在曲线C(曲线C为正态分布N(－2，4)的密度曲线)与x轴围成的区域中随机投掷10 000个点，则落入阴影部分的点的个数的估计值为(　　)‎ ‎(附：X～N(μ，σ2)，则P(μ－σ0，|φ|<)的部分图象如图所示，点A(0，)，B(，0)，则函数f(x)图象的一条对称轴为(　　)‎ A．x＝－ B．x＝－ C．x＝ D．x＝ ‎9．如图，△AOD是一直角边长为1的等腰直角三角形，平面图形OBD是四分之一圆面，点P在线段AB上，PQ⊥AB，且PQ交AD或交弧DB于点Q，设AP＝x(0＜x＜2)，图中阴影部分表示的平面图形APQ(或APQD)的面积为y，则函数y＝f(x)的大致图象是(　　)‎ ‎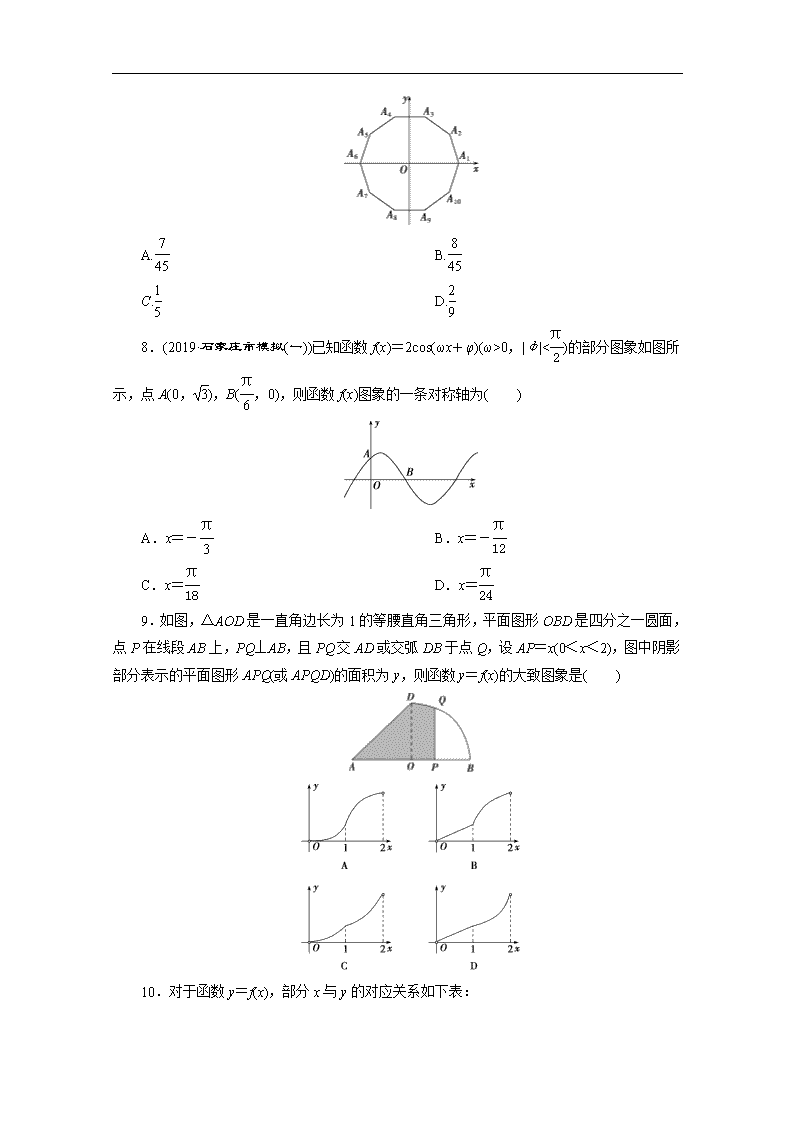10．对于函数y＝f(x)，部分x与y的对应关系如下表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ y ‎3‎ ‎7‎ ‎5‎ ‎9‎ ‎6‎ ‎1‎ ‎8‎ ‎2‎ ‎4‎ 数列{xn}满足：x1＝1，且对于任意n∈N*，点(xn，xn＋1)都在函数y＝f(x)的图象上，则x1＋x2＋…＋x2 018＝(　　)‎ A．7 564 B．7 565 ‎ C．7 566 D．7 569‎ ‎11．(多选)已知定义在R上的函数f(x)，其导函数f′(x)的大致图象如图所示，则下列叙述不正确的是(　　)‎ A．f(a)＞f(e)＞f(d)‎ B．函数f(x)在[a，b]上递增，在[b，d]上递减 C．函数f(x)的极值点为c，e D．函数f(x)的极大值为f(b)‎ ‎12．(多选)某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量(单位：厘米)，图1为选取的15名志愿者身高与臂展的折线图，图2为身高与臂展所对应的散点图，并求得其回归方程为＝1.16x－30.75，以下结论正确的为(　　)‎ 图1‎ 图2‎ A．15名志愿者身高的极差小于臂展的极差 B．15名志愿者身高和臂展成正相关关系 C．可估计身高为190厘米的人臂展大约为189.65厘米 D．身高相差10厘米的两人臂展都相差11.6厘米 ‎13．(多选)如图，一张A4纸的长、宽分别为2a，2a，A，B，C，D分别是其四条边的中点．现将其沿图中虚线折起，使得P1，P2，P3，P4四点重合为一点P，从而得到一个多面体．下列关于该多面体的命题，正确的是(　　)‎ A．该多面体是三棱锥 B．平面BAD⊥平面BCD C．平面BAC⊥平面ACD D．该多面体外接球的表面积为5πa2‎ 二、填空题 ‎14．已知某区中小学学生人数如图所示．为了解该区学生参加某项社会实践活动的意向，拟采用分层抽样的方法来进行调查．若高中需抽取20名学生，则小学与初中共需抽取的学生人数为________．‎ ‎15．某市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛(河南初赛)，他们取得的成绩(满分140分)的茎叶图如图所示，其中甲班学生成绩的中位数是81，乙班学生成绩的平均数是86.若正实数a，b满足a，G，b成等差数列且x，G，y成等比数列，则＋的最小值为________．‎ ‎16．已知某次考试之后，班主任从全班同学中随机抽取一个容量为8的样本，他们的数学、物理成绩(单位：分)对应如下表：‎ 学生编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 数学成绩 ‎60‎ ‎65‎ ‎70‎ ‎75‎ ‎80‎ ‎85‎ ‎90‎ ‎95‎ 物理成绩 ‎72‎ ‎77‎ ‎80‎ ‎84‎ ‎88‎ ‎90‎ ‎93‎ ‎95‎ 给出散点图如下：‎ 根据以上信息，判断下列结论：‎ ‎①根据散点图，可以判断数学成绩与物理成绩具有线性相关关系；‎ ‎②根据散点图，可以判断数学成绩与物理成绩具有一次函数关系；‎ ‎③从全班随机抽取甲、乙两名同学，若甲同学数学成绩为80分，乙同学数学成绩为60分，则甲同学的物理成绩一定比乙同学的物理成绩高．‎ 其中正确的个数为________．‎ ‎17．某食品的保鲜时间t(单位：小时)与储藏温度x(恒温，单位：℃)满足函数关系t(x)＝且该食品在4 ℃的保鲜时间是16小时．‎ ‎①该食品在8 ℃的保鲜时间是________小时；‎ ‎②已知甲在某日上午10时购买了该食品，并将其遗放在室外，且此日的室外温度随时间变化如图所示，那么到了此日13时，甲所购买的食品________保鲜时间(填“过了”或“没过”)．‎ ‎ ‎ 小题分类练(四)　图表信息类 ‎1．解析：选B.由x2＋x－6＝0得x＝－3或x＝2，所以B＝{－3，2}，A＝{1，2，3，4，‎ ‎5，6}，所以(∁ZA)∩B＝{－3}，故选B.‎ ‎2．解析：选D.由茎叶图可得甲的成绩的平均数为 ＝21.将乙的成绩按从小到大的顺序排列，中间的两个成绩分别是22，23，所以乙的成绩的中位数为＝22.5.‎ ‎3．解析：选B.根据题意，依次分析选项，A中，由该城市的各月最低温与最高温具有相关关系及数据分析可得最低温与最高温为正相关，故A正确；B中，由表中数据，每月最高温与最低温的平均值依次为－3.5、3、5、4.5、12、20.5、23、26.5、28、15.5，在前8个月不是逐月增加，故B错误；C中，由表中数据，月温差依次为17、12、8、13、10、7、8、7、6、11，月温差的最大值出现在1月，故C正确；D中，分析可得1至4月的月温差相对于7至10月，波动性更大，故D正确．故选B.‎ ‎4．解析：选C.对于A，对比四个季度中，第4季度所销售的电视机所占百分比最大，但由于销售总量未知，所以销量不一定最大．对于B，理由同A.在四个季度中，电视机在每个季度销量所占百分比都最大，即在每个季度销量都是最多的，所以全年销量最大的是电视机，C正确，D错误．‎ ‎5．解析：选C.因为x～N(－2，4)，所以正态曲线关于直线x＝－2对称，且μ＝－2，σ＝2.因为P(μ－σ0，所以φ<0，所以φ＝－，所以f(x)＝2cos(ωx－)．因为f(x)＝2cos(ωx－)的图象过点B(，0)‎ ‎，所以cos＝0，所以＝mπ＋(m∈Z)，所以ω＝6m＋4(m∈Z)，因为ω>0，>，所以0<ω<6，所以ω＝4，所以f(x)＝2cos(4x－)．因为x＝时，f(x)＝2，所以x＝为函数f(x)图象的一条对称轴，故选D.‎ ‎9．解析：选A.观察可知阴影部分的面积y的变化情况为：①当0＜x≤1时，y随x的增大而增大，而且增加的速度越来越快；②当1＜x＜2时，y随x的增大而增大，而且增加的速度越来越慢．分析四个选项中的图象，只有选项A符合条件，故选A.‎ ‎10．解析：选A.因为数列{xn}满足x1＝1，且对任意n∈N*，点(xn，xn＋1)都在函数y＝f(x)的图象上，所以xn＋1＝f(xn)，所以由图表可得x2＝f(x1)＝3，x3＝f(x2)＝5，x4＝f(x3)＝6，x5＝f(x4)＝1，…，所以数列{xn}是周期为4的周期数列，所以x1＋x2＋…＋x2 018＝504(x1＋x2＋x3＋x4)＋x1＋x2＝504×15＋1＋3＝7 564.故选A.‎ ‎11．解析：选ABD.由图可知，当x∈(－∞，c)时，f′(x)＞0，当x∈(c，e)时，f′(x)＜0，当x∈(e，＋∞)时，f′(x)＞0，所以f(x)在(－∞，c)上递增，在(c，e)上递减，在(e，＋∞)上递增，所以f(d)＞f(e)，故A错误；函数f(x)在[a，b]上递增，在[b，c]上递增，在[c，d]上递减，故B错误；函数f(x)的极值点为c，e，故C正确；函数f(x)的极大值为f(c)，故D错误．‎ ‎12．解析：选ABC.对于A，根据折线图可知，身高极差小于20，臂展极差大于20，故A正确；‎ 对于B，很明显根据散点图以及回归方程得到，身高矮展臂就会短一些，身高高一些，展臂就会长一些，故B正确；‎ 对于C，身高为190厘米，代入回归方程可得展臂等于189.65厘米，但不是准确值，故C正确；‎ 对于D，身高相差10厘米的两个展臂的估计值相差11.6厘米，但不是准确值，回归方程上的点并不都是准确的样本点，故D错误．‎ ‎13．解析：选ABCD.由题意得该多面体是一个三棱锥，故A正确；因为AP⊥BP，AP⊥CP，BP∩CP＝P，所以AP⊥平面BCD，又因为AP⊂平面BAD，所以平面BAD⊥平面BCD，故B正确；同理可证平面BAC⊥平面ACD，故C正确；通过构造长方体可得该多面体的外接球半径R＝a，所以该多面体外接球的表面积为5πa2，故D正确．综上，正确命题为ABCD.‎ ‎14．解析：设小学与初中共需抽取的学生人数为x，依题意可得＝，解得x＝85.‎ 答案：85‎ ‎15．解析：由甲班学生成绩的中位数是81，‎ 可知81为甲班7名学生的成绩按从小到大的顺序排列的第4个数，故x＝1.由乙班学生成绩的平均数为86，可得(－10)＋(－6)＋(－4)＋(y－6)＋5＋7＋10＝0，解得y＝4.由x，G，y成等比数列，可得G2＝xy＝4，可得G＝2，由正实数a，b满足a，G，b成等差数列，可得a＋b＝2G＝4，所以＋＝×＝≥×(5＋4)＝(当且仅当b＝2a时取等号)．故＋的最小值为.‎ 答案： ‎16．解析：由散点图知，各点都分布在一条直线附近，故可以判断数学成绩与物理成绩具有线性相关关系，但不能判断数学成绩与物理成绩具有一次函数关系，故①正确，②错误；若甲同学数学成绩为80分，乙同学数学成绩为60分，则甲同学的物理成绩可能比乙同学的物理成绩高，故③错误．综上，正确的个数为1.‎ 答案：1‎ ‎17．解析：①因为食品在4 ℃的保鲜时间是16小时，所以24k＋6＝16，解得k＝－.‎ 所以t(8)＝2－4＋6＝4；‎ ‎②由图象可知在11时之前，温度已经超过了10 ℃，此时该食品的保鲜期少于21＝2小时，而食品在11时之前已放了一段时间，所以到13时，该食品已过保鲜期．‎ 答案：①4　②过了