2009年江苏省高考数学试卷【word版本、可编辑、附详细答案和解释】 6页

‎2009年江苏省高考数学试卷 一、填空题（共13小题，每小题5分，满分65分）‎ ‎1. 若复数z‎1‎‎=4+29i，z‎2‎‎=6+9i，其中i是虚数单位，则复数‎(z‎1‎-z‎2‎)i的实部为________．‎ ‎2. 已知向量a‎→‎和向量b‎→‎的夹角为‎30‎‎0‎，‎|a‎→‎|=2，|b‎→‎|=‎‎3‎，则向量a‎→‎和向量b‎→‎的数量积a‎→‎‎⋅b‎→‎=‎________．‎ ‎3. 函数f(x)=x‎3‎-15x‎2‎-33x+6‎的单调减区间为________．‎ ‎4. 函数y=Asin(ωx+φ)(A，ω，φ为常数，A>0‎，ω>0)‎在闭区间‎[-π, 0]‎的图象如图所示，则ω=‎________．‎ ‎5. 现有‎5‎根竹竿，它们的长度（单位：m）分别为‎2.5‎，‎2.6‎，‎2.7‎，‎2.8‎，‎2.9‎，若从中一次随机抽取‎2‎根竹竿，则它们的长度恰好相差‎0.3m的概率为________．‎ ‎6. 某校甲、乙两个班级各有‎5‎名编号为‎1‎，‎2‎，‎3‎，‎4‎，‎5‎的学生进行投篮练习，每人投‎10‎次，投中的次数如表：‎ 学生 ‎1‎号 ‎2‎号 ‎3‎号 ‎4‎号 ‎5‎号 甲班 ‎6‎ ‎7‎ ‎7‎ ‎8‎ ‎7‎ 乙班 ‎6‎ ‎7‎ ‎6‎ ‎7‎ ‎9‎ 则以上两组数据的方差中较小的一个为S‎2‎‎=‎________．‎ ‎7. 如图是一个算法的流程图，最后输出的W=‎________．‎ ‎8. 在平面直角坐标系xOy中，点P在曲线C:y=x‎3‎-10x+3‎上，且在第二象限内，已知曲线C在点P处的切线斜率为‎2‎，则点P的坐标为________．‎ ‎9. 已知a=‎‎5‎‎-1‎‎2‎，函数f(x)=‎logax，若正实数m，n满足f(m)>f(n)‎，则m，n的大小关系为________．‎ ‎10. 已知集合A={x|log‎2‎x≤2}‎，B=(-∞, a)‎，若A⊆B则实数a的取值范围是‎(c, +∞)‎，其中c=‎________．‎ ‎11. 设α和β为不重合的两个平面，给出下列命题：‎ ‎（1）若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；‎ ‎（2）若α外一条直线l与α内的一条直线平行，则l和α平行；‎ ‎（3）设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；‎ ‎（4）直线l与α垂直的充分必要条件是l与α内的两条直线垂直．‎ 上面命题，真命题的序号是________‎ ‎12. 如图，在平面直角坐标系xoy中，A‎1‎，A‎2‎，B‎1‎，B‎2‎为椭圆x‎2‎a‎2‎‎+y‎2‎b‎2‎=1(a>b>0)‎的四个顶点，F为其右焦点，直线A‎1‎B‎2‎与直线B‎1‎F相交于点T，线段OT与椭圆的交点M恰为线段OT 第9页 共12页 ◎ 第10页 共12页 的中点，则该椭圆的离心率为________．‎ ‎13. 设‎{an}‎是公比为q的等比数列，‎|q|>1‎，令bn‎=an+1(n=1, 2‎,…‎)‎，若数列‎{bn}‎有连续四项在集合‎{-53, -23, 19, 37, 82}‎中，则‎6q=‎________．‎ 二、解答题（共7小题，满分95分）‎ ‎14. 在平面上，若两个正三角形的边长的比为‎1:2‎，则它们的面积比为‎1:4‎，类似地，在空间内，若两个正四面体的棱长的比为‎1:2‎，则它们的体积比为________．‎ ‎15. 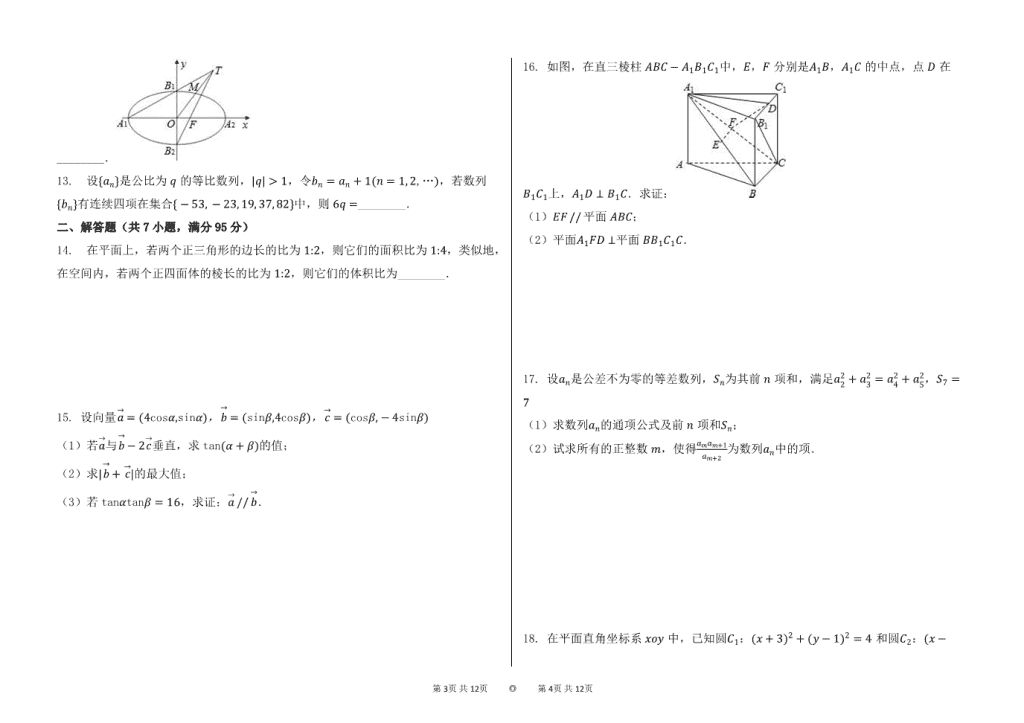设向量a‎→‎‎=(4cosα,sinα)，b‎→‎=(sinβ,4cosβ)，c‎→‎=(cosβ,-4sinβ)‎ ‎（1）若a‎→‎与b‎→‎‎-2‎c‎→‎垂直，求tan(α+β)‎的值；‎ ‎（2）求‎|b‎→‎+c‎→‎|‎的最大值；‎ ‎（3）若tanαtanβ=16‎，求证：a‎→‎‎ // ‎b‎→‎．‎ ‎16. 如图，在直三棱柱ABC-‎A‎1‎B‎1‎C‎1‎中，E，F分别是A‎1‎B，A‎1‎C的中点，点D在B‎1‎C‎1‎上，A‎1‎D⊥B‎1‎C．求证：‎ ‎（1）EF // ‎平面ABC；‎ ‎（2）平面A‎1‎FD⊥‎平面BB‎1‎C‎1‎C．‎ ‎17. 设an是公差不为零的等差数列，Sn为其前n项和，满足a‎2‎‎2‎‎+a‎3‎‎2‎=a‎4‎‎2‎+‎a‎5‎‎2‎，‎S‎7‎‎=7‎ ‎（1）求数列an的通项公式及前n项和Sn；‎ ‎（2）试求所有的正整数m，使得amam+1‎am+2‎为数列an中的项．‎ 第9页 共12页 ◎ 第10页 共12页 ‎18. 在平面直角坐标系xoy中，已知圆C‎1‎：‎(x+3‎)‎‎2‎+(y-1‎)‎‎2‎=4‎和圆C‎2‎：‎‎(x-4‎)‎‎2‎+(y-5‎)‎‎2‎=4‎ ‎（1）若直线l过点A(4, 0)‎，且被圆C‎1‎截得的弦长为‎2‎‎3‎，求直线l的方程；‎ ‎（2）设P(a, b)‎为平面上的点，满足：存在过点P的两条互相垂的直线l‎1‎与l‎2‎，l‎1‎的斜率为‎2‎，它们分别与圆C‎1‎和圆C‎2‎相交，且直线l‎1‎被圆C‎1‎截得的弦长与直线l‎2‎被圆C‎2‎截得的弦长相等，试求满足条件的a，b的关系式．‎ ‎19. 照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为 m元，则他的满意度为mm+a；如果他买进该产品的单价为n元，则他的满意度为an+a．如果一个人对两种交易（卖出或买进）的满意度分别为h‎1‎和h‎2‎，则他对这两种交易的综合满意度为h‎1‎h‎2‎．‎ 现假设甲生产A、B两种产品的单件成本分别为‎12‎元和‎5‎元，乙生产A、B两种产品的单件成本分别为‎3‎元和‎20‎元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙．‎ ‎（1）求h甲和h乙关于mA、mB的表达式；当mA‎=‎‎3‎‎5‎mB时，求证：h甲＝h乙；‎ ‎（2）设mA‎=‎‎3‎‎5‎mB，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？‎ ‎（3）记（2）中最大的综合满意度为h‎0‎，试问能否适当选取mA、mB的值，使得h甲‎≥‎h‎0‎和h乙‎≥‎h‎0‎ 同时成立，但等号不同时成立？试说明理由．‎ ‎20. 设a为实数，函数f(x)=2x‎2‎+(x-a)|x-a|‎．‎ ‎(1)‎若f(0)≥1‎，求a的取值范围；‎ ‎(2)‎求f(x)‎的最小值；‎ ‎(3)‎设函数h(x)=f(x)‎，x∈(a, +∞)‎，求不等式h(x)≥1‎的解集．‎ 第9页 共12页 ◎ 第10页 共12页 参考答案与试题解析 ‎2009年江苏省高考数学试卷 一、填空题（共13小题，每小题5分，满分65分）‎ ‎1.‎‎-20‎ ‎2.‎‎3‎ ‎3.‎‎(-1, 11)‎ ‎4.‎‎3‎ ‎5.‎‎0.2‎ ‎6.‎‎0.4‎ ‎7.‎‎22‎ ‎8.‎‎(-2, 15)‎ ‎9.‎m0‎），当mA‎=‎‎3‎‎5‎mB时，‎ h甲‎＝h乙‎=‎20x‎(x+5)(x+20)‎=‎20‎x+‎100‎x+25‎≤‎‎2‎‎3‎；‎ 当且仅当x=‎‎100‎x，即x＝‎10‎时，上式“＝”成立，即mB＝‎10‎，mA‎=‎3‎‎5‎×10‎＝‎6‎时，‎ 甲、乙两人的综合满意度均最大，最大综合满意度为‎2‎‎3‎；‎ 任取mA＝‎5‎，mB＝‎10‎，则h甲‎≈0.686‎，h乙‎≈0.645‎．‎ 不能由（2）知h‎0‎‎=‎2‎‎3‎≈0.667‎．因为h甲h乙‎≤‎‎4‎‎9‎ 因此，不能取到mA，mB的值，使得h甲‎≥‎h‎0‎和h乙‎≥‎h‎0‎同时成立，但等号不同时成立．‎ ‎20.解：‎(1)‎若f(0)≥1‎，‎ 则‎-a⋅|a|≥1⇒a<0‎a‎2‎‎≥1‎⇒a≤-1‎；‎ ‎(2)‎当x≥a时，f(x)=3x‎2‎-2ax+‎a‎2‎，‎ ‎∴ ‎f(x‎)‎min=f(a)，a≥0‎f(a‎3‎)，a<0‎=‎‎2a‎2‎，a≥0，‎‎2‎‎3‎a‎2‎‎，a<0，‎ 如图所示：‎ 当x≤a时，f(x)=x‎2‎+2ax-‎a‎2‎，‎ ‎∴ ‎f(x‎)‎min=f(-a),a≥0‎f(a),a<0‎=‎‎-2a‎2‎，a≥0，‎‎2a‎2‎，a<0，‎ 综上所述：‎f(x‎)‎min=‎‎-2a‎2‎，a≥0，‎‎2‎‎3‎a‎2‎‎，a<0.‎ ‎(3)x∈(a, +∞)‎时，h(x)≥1‎，‎ 第9页 共12页 ◎ 第10页 共12页 得‎3x‎2‎-2ax+a‎2‎-1≥0‎，‎ Δ=4a‎2‎-12(a‎2‎-1)=12-8‎a‎2‎‎.‎ 当a≤-‎‎6‎‎2‎或a≥‎‎6‎‎2‎时，‎ Δ≤0‎‎，‎ 当‎-‎6‎‎2‎0‎‎.‎ 得：‎‎(x-a-‎‎3-2‎a‎2‎‎3‎)(x-a+‎‎3-2‎a‎2‎‎3‎)≥0,‎x>a,‎ 即x≤a-‎‎3-2‎a‎2‎‎3‎或x≥a+‎‎3-2‎a‎2‎‎3‎，‎x>a，‎ 进而分两类讨论：‎ 当‎-‎6‎‎2‎