新教材数学人教B版必修第二册课件：6-2-3 向量的数乘运算 39页

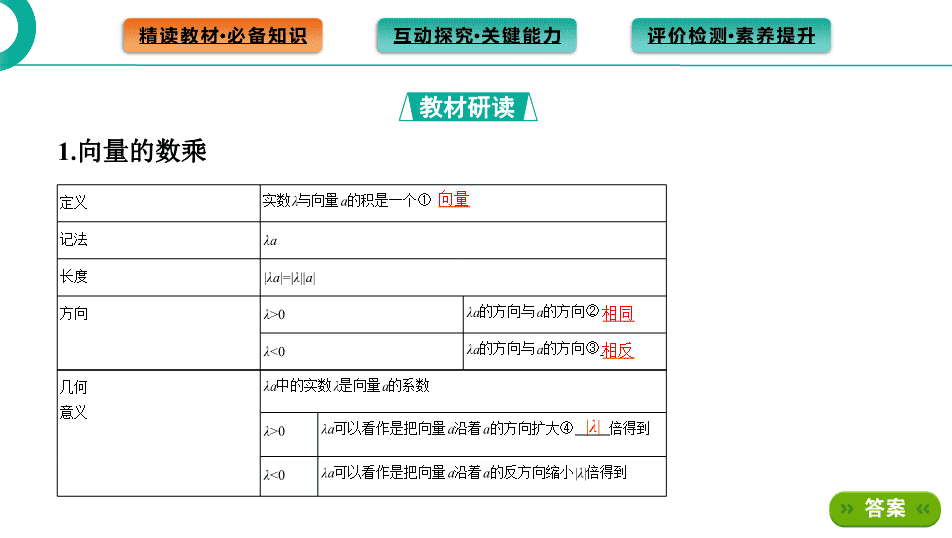
精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 第六章　平面向量及其应用 §6.2　平面向量的运算 6.2.3　向量的数乘运算 第 一 篇 教 材 过 关 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 一只兔子第1秒钟向东跑了2米,第2、3秒钟又向东各跑了2米. 问题1:兔子3秒的位移一共是多少? 情景导学 精读教材·必备知识 答案　设兔子第1秒的位移是向量a,则3秒的位移是向量3a. 问题2:若兔子向西跑3秒,则向量是多少? 答案　-3a(用a表示向东跑1秒). 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.向量的数乘 教材研读 定义 实数λ与向量a的积是一个① 记法 λa 长度 |λa|=|λ||a| 方向 λ>0 λa的方向与a的方向② λ<0 λa的方向与a的方向③ 向量 相同 相反 几何 意义 λa中的实数λ是向量a的系数 λ>0 λa可以看作是把向量a沿着a的方向扩大④ 倍得到 λ<0 λa可以看作是把向量a沿着a的反方向缩小|λ|倍得到 |λ| 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 特别提醒 当λ=0时,λa=0.当λ≠0时,若a=0,也有λa=0. 思考1:实数与向量能否进行加减运算? 提示　不能. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.向量的数乘运算的运算律 设λ,μ为实数,那么 (1)λ(μa)=(λμ)a; (2)(λ+μ)a=⑤ ; (3)λ(a+b)=λa+λb. 思考2:向量数乘运算律与实数乘法运算律有什么关系? λa+μa 提示　两种运算律类似,(2)(3)式是向量因式不同的分配律. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.向量的线性运算 (1)向量的加、减、数乘运算统称为向量的线性运算,向量线性运算的结果仍 是⑥ . (2)对于任意向量a,b以及任意实数λ、μ1、μ2,恒有λ(μ1a±μ2b)=λμ1a±λμ2b. 思考3:向量的线性运算法则与实数的运算法则有什么关系? 向量 提示　在形式上类似. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.共线向量定理 向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使⑦ . 思考4:λ与向量a,b的方向有什么关系? b=λa 提示　若λ>0,则a与b同向;若λ<0,则a与b反向. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究一　向量的线性运算 互动探究·关键能力 例1　(1)化简下列各式: ①3(6a+b)-9  ; ②   -2  ; ③2(5a-4b+c)-3(a-3b+c)-7a. (2)已知向量a,b,m,n满足a=3m+2n,b=m-3n,试用向量a,b表示向量m,n. 1 3 a b     1 2 13 2 - 2 a b a b        1 3 2 8 a b     精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)①原式=18a+3b-9a-3b=9a. ②原式=   -a- b=a+ b-a- b=0. ③原式=10a-8b+2c-3a+9b-3c-7a=b-c. (2)a=3m+2n①,b=m-3n②, 则①×3+②×2得3a+2b=11m, 即m= a+ b. ①-②×3得a-3b=11n, 1 2 32 2 a b     3 4 3 4 3 4 3 11 2 11 即n= a- b. 1 11 3 11 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 向量的线性运算的技巧 向量的线性运算类似于代数多项式的运算. (1)实数运算中去括号、移项、合并同类项、提取公因式等方法在向量线性 运算中也可以使用. (2)这里的“同类项”“公因式”指向量,实数看作是向量的系数. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 1-1　化简下列各式: (1)2(3a-2b)+3(a+5b)-5(4b-a); (2) [2(2a+8b)-4(4a-2b)]; (3)(m+n)(a-b)-(m-n)(a+b). 1 6 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)原式=6a-4b+3a+15b-20b+5a=14a-9b. (2)原式= ×(4a+16b-16a+8b)= ×(-12a+24b)=-2a+4b. (3)原式=m(a-b)+n(a-b)-m(a+b)+n(a+b) =(m+n-m+n)a+(-m-n-m+n)b =2na-2mb. 1 6 1 6 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究二　共线向量定理及其应用 例2　设两个非零向量a与b不共线. (1)若  =a+b,  =2a+8b,  =3(a-b),求证:A、B、D三点共线; (2)试确定实数k,使ka+b与a+kb共线. AB  BC  CD  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)证明:∵  =a+b,  =2a+8b,   =3(a-b), ∴  =  +  =2a+8b+3(a-b)=2a+8b+3a-3b=5(a+b)=5  . ∴  、  共线, 又∵  与  有公共点B,∴A、B、D三点共线. (2)∵ka+b与a+kb共线,∴存在实数λ,使ka+b=λ(a+kb), AB  BC  CD  BD  BC  CD  AB  AB  BD  AB  BD  即ka+b=λa+λkb,∴(k-λ)a=(λk-1)b. ∵a、b是不共线的两个非零向量, ∴k-λ=λk-1=0,∴k2-1=0,∴k=±1. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 用向量法证明三点共线的关键与步骤 (1)关键:能否找到一个实数λ,使得b=λa(a、b为这三点构成的任意两个向量). (2)步骤:先证明向量共线,然后指出两向量有公共点,从而证得三点共线. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 2-1　如图,在平行四边形ABCD中,点M是AB的中点,点N在线段BD上,且有BN=  BD,求证:M,N,C三点共线.   1 3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 证明　设  =a,  =b,则  =  +  =   +   =   + (  -  )= a+ (b -a)= a+ b,  =  +  =   +  = a+b=3×  =3  ,∴  ,  共线, AB  BC  MN  MB  BN  1 2 AB  1 3 BD  1 2 AB  1 3 AD  AB  1 2 1 3 1 6 1 3 MC  MB  BC  1 2 AB  BC  1 2 1 1 6 3 a b     MN  MC  MN  又  与  有公共点M,∴M,N,C三点共线. MC  MN  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究三　向量线性运算的应用 例3 (易错题)已知点E,F分别为四边形ABCD的对角线AC,BD的中点,设  =a,   =b,试用a,b表示  .   BC  DA  EF  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　如图所示,取AB的中点P,连接EP,FP.   在△ABC中,EP是中位线, 所以  =   = a. 在△ABD中,FP是中位线, PE  1 2 BC  1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 所以  =   =-   =- b. 在△EFP中,  =  +  =-  +  =- ·a- b =- (a+b). PF  1 2 AD  1 2 DA  1 2 EF  EP  PF  PE  PF  1 2 1 2 1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 易错点拨 在根据平面几何图形进行化简、证明时,要准确应用平面几何图形的性质.应 根据题意判断所给图形是不是特殊图形,不能盲目运用特殊图形的性质进行 求解. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 3-1　已知四边形ABCD是一个梯形,AB∥CD,且AB=2CD,M,N分别是DC,AB的 中点,已知  =a,  =b,试用a,b表示  和  .   AB  AD  BC  MN  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　解法一:如图,连接CN,   易知AN DC, 所以四边形ANCD是平行四边形.   =-  =-b,又因为  +  +  =0, 所以  =-  -  =b- a, CN  AD  CN  NB  BC  BC  CN  NB  1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升   =  -  =  +   =-b+ a. 解法二:因为  +  +  +  =0, 所以a+  +  +(-b)=0, 所以  =b- a, 又因为在四边形ADMN中有   +  +  +  =0, 所以b+ a+  +  =0, MN  CN  CM  CN  1 2 AN  1 4 AB  BC  CD  DA  BC  1- 2 a      BC  1 2 AD  DM  MN  NA  1 4 MN  1- 2 a      所以  = a-b.MN  1 4 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3-2　设O为△ABC内任意一点,且满足  +2  +3  =0,若D,E分别是BC,CA的 中点. (1)求证:D,E,O三点共线; (2)求  的值. OA  OB  OC  ABC AOC S S   精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)证明:如图,  +  = 2  ,  +  =2  , ∴  +2  +3  =(  +  )+2(  +  )=2(2  +  )=0, ∴2  +  =0,∴  与  共线, 又  与  有公共点O, ∴D,E,O三点共线.   OB  OC  OD  OA  OC  OE  OA  OB  OC  OA  OC  OB  OC  OD  OE  OD  OE  OD  OE  OD  OE  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 (2)由(1)知2|  |=|  |, ∴S△AOC=2S△COE=2× S△CDE=2× × ×S△ABC= S△ABC, ∴  =3. OD  OE  2 3 2 3 1 4 1 3 ABC AOC S S   精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.已知非零向量a,b满足a=4b,则  (　　) A.|a|=|b| B.4|a|=|b| C.a,b的方向相同 D.a,b的方向相反 课堂检测 评价检测·素养提升 解析　∵a=4b,4>0,∴|a|=4|b|. ∵4b与b的方向相同,∴a与b的方向相同. C 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.(多选题)下列向量中,a,b一定共线的是  (　 　) A.a=2e,b=-2e B.a=e1-e2,b=-2e1+2e2 C.a=4e1- e2,b=e1- e2 2 5 1 10 D.a=e1+e2,b=2e1-2e2 解析 A中,b=-a,则a,b共线;B中,b=-2a,则a,b共线;C中,a=4b,则a,b共线; D中,a,b不共线. ABC 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.已知向量a=e1+λe2,b=2e1,λ∈R,且λ≠0,若a∥b,则  (　 　) A.e1=0　　B.e2=0 C.e1∥e2　　D.e1∥e2或e1=0或e2=0 D 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.已知x,y是实数,向量a,b不共线,若(x+y-1)a+(x-y)b=0,则x=　　　 , y=　　 . 解析　由已知得  解得x=y= . -1 0, - 0, x y x y     1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 5.已知两个非零向量e1、e2不共线,若  =2e1+3e2,  =6e1+23e2,  =4e1-8e2.求 证:A、B、D三点共线. AB  BC  CD  证明　∵  =  +  +  AD  AB  BC  CD  =2e1+3e2+6e1+23e2+4e1-8e2 =12e1+18e2=6(2e1+3e2)=6  , ∴  ,  共线. 又∵  和  有公共点A, ∴A、B、D三点共线. AB  AD  AB  AD  AB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 数学运算——在几何图形中进行向量线性运算 如图所示,已知▱ ABCD的边BC,CD上的中点分别为K,L,且  =e1,  =e2,试用e1, e2表示  ,  .   审:几何图形中用已知向量表示待求向量,可考虑用三角形法则或共线定理. AK  AL  BC  CD  素养演练 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 联:结合图形特征,把待求向量放在三角形中,进行加减运算. 解:解法一:设  =a,则  =①　　 　 ,BC  BK    =  +  =e1- a,  = e1- a. AB  AK  KB  1 2 DL  1 2 1 4 又  =  =a,由  +  =  ,得a+ e1- a=e2, 解得a=②　　　　　 　　　　 . AD  BC  AD  DL  AL  1 2 1 4 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 由  =-  ,  =e1- a,得   =③　　　 . 解法二:设  =m,  =n,则  = m,  =- n. 由  +  =  ,  +  =  , 得④　　　　　 　 , CD  AB  AB  1 2 CD  BC  CD  BK  1 2 DL  1 2 AB  BK  AK  AD  DL  AL  得m= (2e2-e1),n=⑤　　　　 　　 , 2 3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 即  = e2- e1,  =- e1+ e2. 解法三:如图所示,BC的延长线与AL的延长线交于点E,则△DLA≌ △CLE.   从而  =2  ,  =  =  ,  =   , BC  4 3 2 3 CD  4 3 2 3 AE  AL  CE  AD  BC  KE  3 2 BC  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 由  =  -  ,得   =2e2-e1, 即  =⑥　　　　　　　 . 同理可得  =⑦　　　　　　 　 . 思:解决此类问题的一般思路是将所表示向量置于某一个三角形内,用加减法 进行运算,然后逐步用已知向量表示待求向量,过程中体现数学运算核心素养. KE  AE  AK  3 2 BC  BC  CD  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 针对训练 　如图所示,四边形OADB是以向量  =a,  =b为邻边的平行四边形,又BM=  BC,CN= CD,试用a,b表示  、  、  .   OA  OB  1 3 1 3 OM  ON  MN  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析   =   =   = (  -  )= (a-b)= a- b, ∴  =  +  =b+ a- b= a+ b. ∵  =   =   , ∴  =  +  =   +   =   = (  +  )= a+ b,   =  -  = a+ b- a- b= a- b. BM  1 3 BC  1 6 BA  1 6 OA  OB  1 6 1 6 1 6 OM  OB  BM  1 6 1 6 1 6 5 6 CN  1 3 CD  1 6 OD  ON  OC  CN  1 2 OD  1 6 OD  2 3 OD  2 3 OA  OB  2 3 2 3 MN  ON  OM  2 3 2 3 1 6 5 6 1 2 1 6