2019-2020学年高中数学课时作业12圆的参数方程北师大版选修4-4 6页

课时作业(十二)‎ ‎1．参数方程(θ为参数)表示的图形是(　　)‎ A．圆心为(－3，3)，半径为9的圆 B．圆心为(－3，3)，半径为3的圆 C．圆心为(3，－3)，半径为9的圆 D．圆心为(3，－3)，半径为3的圆 答案　D 解析　由圆的参数方程可知选D.‎ ‎2．已知圆O的参数方程是(θ为参数，0≤θ<2π)，如果圆上的点A的坐标是(，－)，则点A所对应的参数是________．‎ 答案　π 解析　把点A的坐标(，－)代入参数方程，得解得θ＝π.‎ ‎3．参数方程(θ为参数，0≤θ<2π)表示的曲线是________．‎ 答案　以原点为圆心，半径为5的圆 解析　把参数方程化为则此方程表示圆心为原点，半径为5的圆．‎ ‎4．直线3x＋4y－5＝0与圆(θ为参数，0≤θ<2π)的位置关系是________．‎ 答案　相交 解析　由圆的参数方程，知圆的圆心为原点，半径为，圆心到直线3x＋4y－5＝0的距离d＝＝1<.‎ ‎5．已知圆C的参数方程为(θ为参数)，则点P(4，4)与圆C上的点的最远距离是________．‎ 答案　6‎ 解析　由圆的参数方程，知圆C的圆心为(1，0)，半径为1，则点P与圆心的距离为d＝＝5，则点P(4，4)与圆C上的点的最远距离为5＋1＝6.‎ 6‎ ‎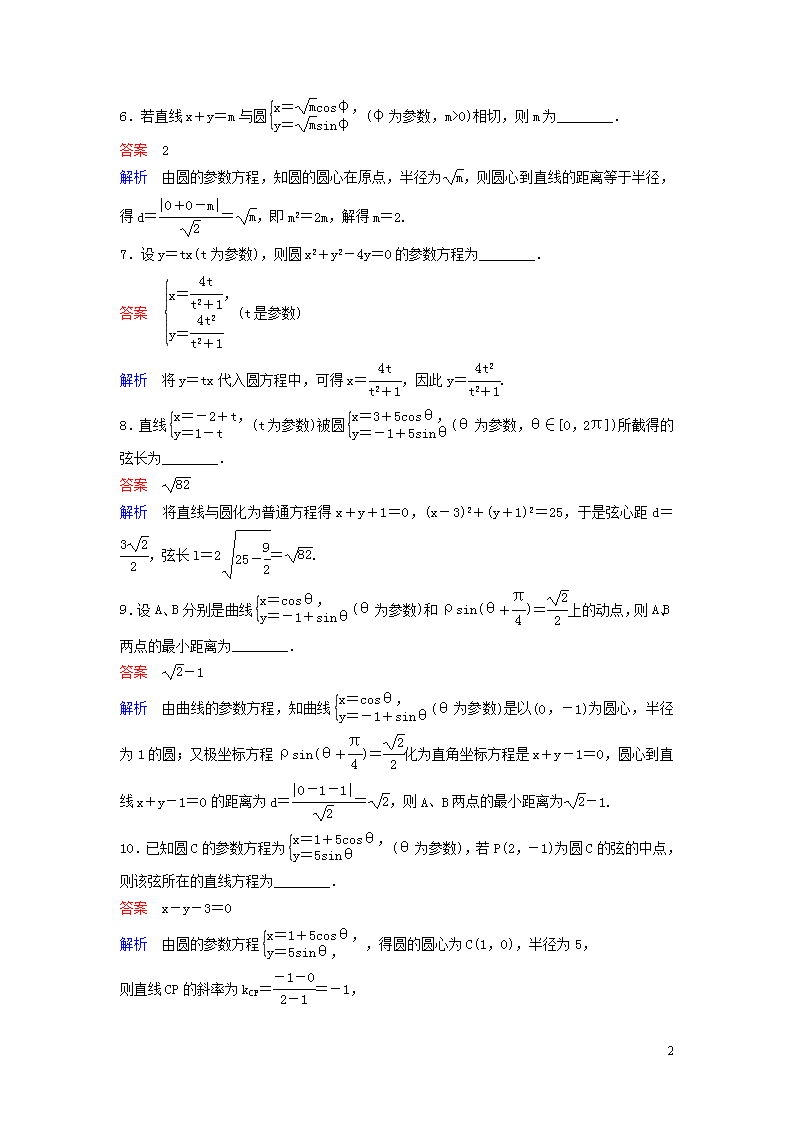6．若直线x＋y＝m与圆(φ为参数，m>0)相切，则m为________．‎ 答案　2‎ 解析　由圆的参数方程，知圆的圆心在原点，半径为，则圆心到直线的距离等于半径，得d＝＝，即m2＝2m，解得m＝2.‎ ‎7．设y＝tx(t为参数)，则圆x2＋y2－4y＝0的参数方程为________．‎ 答案　(t是参数)‎ 解析　将y＝tx代入圆方程中，可得x＝，因此y＝.‎ ‎8．直线(t为参数)被圆(θ为参数，θ∈[0，2π])所截得的弦长为________．‎ 答案　 解析　将直线与圆化为普通方程得x＋y＋1＝0，(x－3)2＋(y＋1)2＝25，于是弦心距d＝，弦长l＝2＝.‎ ‎9．设A、B分别是曲线(θ为参数)和ρsin(θ＋)＝上的动点，则A、B两点的最小距离为________．‎ 答案　－1‎ 解析　由曲线的参数方程，知曲线(θ为参数)是以(0，－1)为圆心，半径为1的圆；又极坐标方程ρsin(θ＋)＝化为直角坐标方程是x＋y－1＝0，圆心到直线x＋y－1＝0的距离为d＝＝，则A、B两点的最小距离为－1.‎ ‎10．已知圆C的参数方程为(θ为参数)，若P(2，－1)为圆C的弦的中点，则该弦所在的直线方程为________．‎ 答案　x－y－3＝0‎ 解析　由圆的参数方程，得圆的圆心为C(1，0)，半径为5，‎ 则直线CP的斜率为kCP＝＝－1，‎ 由弦与CP垂直，得弦所在的直线的斜率为1，‎ 6‎ ‎∴弦所在的直线方程为y－(－1)＝1·(x－2)，即x－y－3＝0.‎ ‎11．在直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线C1：(θ为参数)和曲线C2：ρ＝1上，则|AB|的最小值为________．‎ 答案　3‎ 解析　曲线C1是圆心为(3，4)，半径为1的圆，曲线C2是圆心为(0，0)，半径为1的圆．‎ 所以两圆心之间的距离为 d＝＝5>1＋1，‎ 所以两圆相离，‎ 因为A∈C1，B∈C2，‎ 所以|AB|min＝5－2＝3.‎ ‎12．P(x，y)是曲线(α为参数)上任意一点，则P到直线x－y＋4＝0的距离的最小值是________．‎ 答案　－1＋3 解析　由P在曲线上可得P的坐标为(2＋cosα，sinα)．‎ 由点到直线的距离公式得d＝＝，当cos(α＋)＝－1时，d最小，dmin＝＝－1＋3.‎ ‎13．设方程(θ为参数)表示的曲线为C.‎ ‎(1)求曲线C上的动点到原点O的距离的最小值；‎ ‎(2)点P为曲线C上的动点，当|OP|最小时(O为坐标原点)，求点P的坐标．‎ 解析　(1)设曲线C上任意一点P的坐标为(1＋cosθ，＋sinθ)(0≤θ<2π)，‎ ‎∴|OP|＝＝.‎ ‎∴当θ＝时，|OP|取最小值1.‎ ‎(2)由(1)知当θ＝时，|OP|取最小值，此时1＋cosθ＝1＋cos＝，＋sinθ＝＋sin＝，‎ ‎∴P(，)．‎ 6‎ ‎14．在平面直角坐标系xOy中，曲线C1的参数方程为(θ为参数，且0≤θ≤2π)，点M是曲线C1上的动点．‎ ‎(1)求线段OM的中点P的轨迹的直角坐标方程；‎ ‎(2)以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，若直线l的极坐标方程为ρcosθ－ρsinθ＋1＝0(ρ>0)，求点P到直线l距离的最大值．‎ 解析　(1)曲线C1上的动点M的坐标为(4cosθ，4sinθ)，坐标原点O(0，0)，设P的坐标为(x，y)，则由中点坐标公式，得x＝(0＋4cosθ)＝2cosθ，y＝(0＋4sinθ)＝2sinθ，所以点P的坐标为(2cosθ，2sinθ)．‎ 因此点P的轨迹的参数方程为(θ为参数，且0≤θ≤2π)，消去参数θ得点P的轨迹的直角坐标方程为x2＋y2＝4.‎ ‎(2)由直角坐标与极坐标关系得直线l的直角坐标方程为x－y＋1＝0.‎ 又由(1)知点P的轨迹为圆心在原点半径为2的圆，因为原点(0，0)到直线x－y＋1＝0的距离为＝＝，‎ 所以点P到直线l距离的最大值为2＋.‎ ‎15．在直角坐标系xOy中，圆C的参数方程为(θ为参数)．‎ ‎(1)以原点为极点，x轴正半轴为极轴建立极坐标系，求圆C的极坐标方程；‎ ‎(2)已知A(－2，0)，B(0，2)，圆C上任意一点M(x，y)，求△ABM面积的最大值．‎ 解析　(1)圆C的参数方程为(θ为参数)，‎ ‎∴普通方程为(x－3)2＋(y＋4)2＝4，‎ ‎∴圆C的极坐标方程为ρ2－6ρcosθ＋8ρsinθ＋21＝0.‎ ‎(2)点M(x，y)到直线AB：x－y＋2＝0的距离 d＝，‎ ‎△ABM的面积S＝×|AB|×d＝|2cosθ－2sinθ＋9|＝|2sin(－θ)＋9|，‎ ‎∴△ABM面积的最大值为9＋2.‎ ‎1．直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建极坐标系，设点A，B分别在曲线C1：(θ为参数)和曲线C2：ρ＝2sinθ上，‎ 6‎ 则|AB|的最小值为________．‎ 答案　－2‎ 解析　两个方程分别表示圆：(x－3)2＋y2＝1与x2＋(y－1)2＝1，其圆心距为，两圆相离，故其最短距离为－2.‎ ‎2．已知直线l的参数方程为(t为参数)，圆M的参数方程为(θ为参数)，则直线l被圆M截得的线段的长为________．‎ 答案　2‎ 解析　把圆M的参数方程化为普通方程是x2＋y2＝2；‎ 设t′＝5t，得直线l参数方程的标准形式为 (t′为参数)．‎ 代入圆M的方程x2＋y2＝2，得 ‎(2－t′)2＋(－1＋t′)2＝2，即t′2－4t′＋3＝0，‎ 设直线与圆M的交点A、B对应的参数为t′1，t′2，则 t′1＋t′2＝4，t′1t′2＝3，‎ ‎∴|AB|＝＝2.‎ ‎3．若圆C与直线x－y＝0和直线(t为参数)都相切，且直线x＋y＝0过圆心，则圆C的标准方程为________．‎ 答案　(x－1)2＋(y＋1)2＝2‎ 解析　把直线参数方程消去参数t，得x－y＝4，与直线x－y＝0平行，两直线的距离为d＝＝2.‎ ‎∵圆C与这两直线都相切，∴圆C的半径为.‎ 又直线x＋y＝0过圆心，则圆心坐标满足 ‎∴圆心坐标为(1，－1)，圆C的标准方程为(x－1)2＋(y＋1)2＝2.‎ ‎4．已知直线l的极坐标方程是ρcosθ＋ρsinθ－1＝0.以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，曲线C的参数方程为(θ为参数)．在曲线C上求一点，使它到直线l的距离最小，并求出该点坐标和最小距离．‎ 解析　把直线l的极坐标方程化为直角坐标方程是x＋y－1＝0，由已知曲线C的参数方程，可设曲线C上任意一点的坐标为P(－1＋cosθ，sinθ)，则P到直线l的距离为d＝‎ 6‎ ＝|sin(θ＋)－|，‎ ‎∴当θ＋＝＋2kπ(k∈Z)，即θ＝＋2kπ(k∈Z)时，d有最小值－1，此时，点P的坐标为(－1＋，)．‎ 故在曲线C上点P(－1＋，)到直线l的距离最小，最小距离是－1.‎ 6‎