2020_2021学年新教材高中数学第五章三角函数5 38页

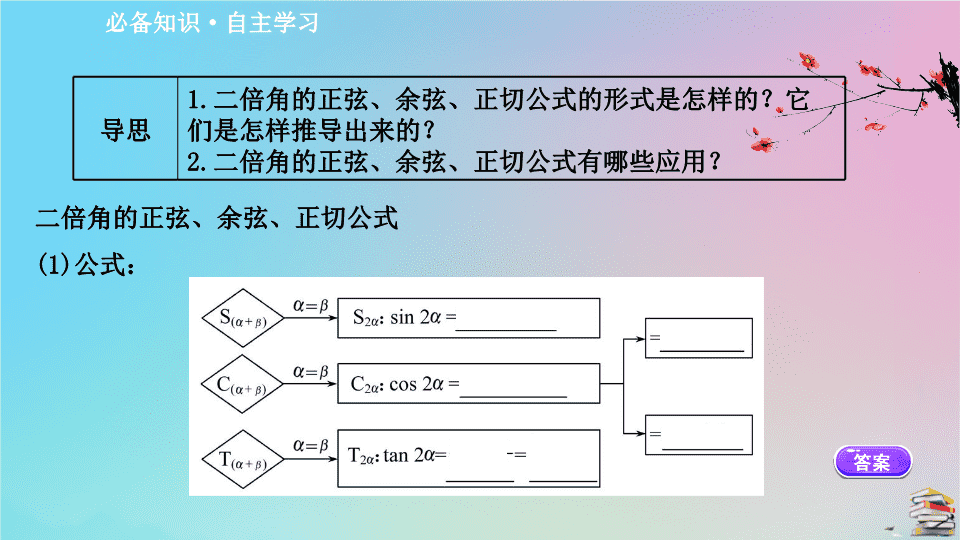
第 4 课时　二倍角的正弦、 余弦、正切公式 必备知识 · 自主学习 二倍角的正弦、余弦、正切公式 (1) 公式： 导思 1. 二倍角的正弦、余弦、正切公式的形式是怎样的？它们是怎样推导出来的？ 2. 二倍角的正弦、余弦、正切公式有哪些应用？ (2) 本质：两角和的正弦、余弦、正切公式，当两角相等时的特殊形式 . (3) 应用：①化简；②求值；③证明 . 【 思考 】 (1) 所谓的“二倍角”公式，一定是角 α 与 2α 之间的转化关系吗？为什么？ 提示： 不一定 . 对于 “ 二倍角 ” 应该广义的理解，如： 8α 是 4α 的二倍角， 3α 是 α 的二倍角， α 是 的二倍角， 是 的二倍角， … ，这里蕴含着换 元思想 . 这就是说 “ 倍 ” 是相对而言的，是描述两个数量之间关系的 . (2) 公式中的角 α 是任意角吗？ 提示： 对于公式 S 2α 、 C 2α 中的角 α 是任意角，但是 T 2α 中的角 α 要保证 tan 2α ， tan α 有意义且分母 1-tan 2 α≠0. 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 二倍角的正切公式的适用范围不是任意角 . ( 　　 ) (2) 对于任意的角 α ，都有 sin 2α=2sin α 成立 . ( 　　 ) (3) 存在角 α ， cos 2α=2cos α 成立 . ( 　　 ) (4)cos 3αsin 3α= sin 6α 对任意的角 α 都成立 . ( 　　 ) 提示： (1)√. 二倍角的正切公式，要求 α≠ +kπ(k∈Z) 且 α≠± +kπ(k∈Z) ，故此说法正确 . (2)×. 当 α= 时， sin 2α=sin = ，而 2sin α=2× =1. (3)√. 由 cos 2α=2cos α=2cos 2 α-1 ，得 cos α= 时， cos 2α= 2cos α 成立 . (4)√. 由二倍角的正弦公式可得 . 2.sin 2 -cos 2 = ( 　　 ) 　　　　　　　　　　　　　　　　　　 【 解析 】 选 D.sin 2 -cos 2 = 3.( 教材二次开发：例题改编 ) 已知 cos α=- ， α∈ ，则 sin 2α= _______ ， cos 2α=_______ ， tan 2α=_______.  【 解析 】 因为 cos α=- ， α∈ ，所以 sin α=- ，所以 sin 2α=2sin αcos α= ， cos 2α=2cos 2 α-1= ， tan 2α= 答案： 　 　 关键能力 · 合作学习 类型一　给角求值问题 ( 数学运算 ) 【 题组训练 】 1. 下列各式中，值为 的是 ( 　　 ) A.2sin 15°cos 15° B.cos 2 15°-sin 2 15° C.2sin 2 15° D.sin 2 15°+cos 2 15° 【 解析 】 1. 选 B.cos 2 15°-sin 2 15°=cos 30°= . 2. 选 B. 原式 = 答案： 1 【 解题策略 】 利用二倍角公式解决给角求值问题的策略 (1) 注意观察式子的结构特点及角之间是否存在特殊的倍数关系，灵活正用或逆用二倍角公式 . (2) 结合诱导公式恰当变化函数名称，灵活处理系数，构造二倍角公式的形式 . 【 补偿训练 】 求下列各式的值： (1) (2)1-2sin 2 750° ； (3) 【 解析 】 (1) 原式 = (2) 原式 =cos(2×750°)=cos 1 500° =cos(4×360°+60°) =cos 60°= . (3) 原式 =tan(2×150°)=tan 300° =tan(360°-60°)=-tan 60°=- . 类型二　条件求值问题 ( 数学运算 ) 【 典例 】 已知 求 cos 的值 . 四步 内容 理解 题意 条件： 结论：求 cos 的值 思路 探求 观察条件中角 的二倍角为 ，而需要求出 sin 2α ， cos 2α 可得结论，故考虑利用二倍角公式及诱导公式解答问题 . 四步 内容 书写 表达 四步 内容 书写 表达 解题注意： ①利用三角函数值的正负、大小缩小角的范围； ②③利用诱导公式变形为已知角的二倍角 . 题后 反思 诱导公式与二倍角公式的灵活运用是解题关键 . 【 解题策略 】 解决条件求值问题的方法 (1) 将已知式或未知式化简，使关系明朗化； (2) 寻找角之间的关系，特别是已知角与要求的角之间的二倍关系，如果二倍关系中含有已知角和某些特殊角，则利用诱导公式转化后整体代入 . 【 跟踪训练 】 已知 tan α+ = ， α∈ ，求 cos 2α 和 sin 的值 . 【 解析 】 【 补偿训练 】 已知 α∈ ，且 sin 2α= 求 α. 【 解析 】 因为 sin 2α=-cos 类型三　化简、证明问题 ( 逻辑推理 ) 　角度 1 　化简问题  【 典例 】 化简： (1) (2) 【 思路导引 】 结合题目特点，利用二倍角的正弦、余弦公式化简 . 【 解析 】 (1) 【 变式探究 】 本例 (2) 若改为： ，试化简 . 【 解析 】 原式 = 　角度 2 　证明问题  【 典例 】 证明： sin 3α=3sin α-4sin 3 α ， cos 3α=4cos 3 α-3cos α. 【 思路导引 】 从等式的左边入手，因为 3α=2α+α ，利用和角公式及二倍角公式展开 . 【 证明 】 sin 3α=sin(2α+α)=sin 2αcos α+cos 2αsin α =2sin αcos 2 α+( 1 － 2sin 2 α )sin α =2sin α( 1 － 2sin 2 α )+( 1 － 2sin 2 α )sin α =3sin α-4sin 3 α ， cos 3α=cos(2α+α)=cos 2αcos α-sin 2αsin α =(2cos 2 α － 1)cos α -2sin 2 α cos α =(2cos 2 α － 1)cos α -2(1 － cos 2 α)cos α =4cos 3 α -3cos α ， 所以 sin 3 α =3sin α -4sin 3 α ， cos 3 α =4cos 3 α -3cos α . 【 解题策略 】 1. 化简三角函数式的常用方法 (1) 切化弦； (2) 异名化同名； (3) 异角化同角； (4) 高次降低次 . 2. 化简三角函数式的常用技巧 (1) 特殊角的三角函数与特殊值的互化； (2) 对于分式形式，应分别对分子、分母进行变形处理，有公因式的提取公因式后进行约分； (3) 对于二次根式，注意倍角公式的逆用； (4) 利用角与角之间的隐含关系，如互余、互补等 . 【 题组训练 】 1.cos 4 -sin 4 的化简结果为 ( 　　 ) 　　　　　　　　　　　　　　　　　　 A.cos B.cos α C.cos 2α D.cos 4α 【 解析 】 选 B.cos 4 -sin 4 = =cos α. 2. 化简 ·cos 28° 的结果为 ( 　　 ) A. B.sin 28° C.2sin 28° D.sin 14°cos 28° 【 解析 】 选 A. · cos 28°= × · cos 28°= tan 28° · cos 28°= . 3. 求证： cos 2 θ(1-tan 2 θ)=cos 2θ. 【 证明 】 方法一：左边 =cos 2 θ =cos 2 θ-sin 2 θ=cos 2θ= 右边，得证 . 方法二：右边 =cos 2θ=cos 2 θ-sin 2 θ =cos 2 θ =cos 2 θ(1-tan 2 θ)= 左边，得证 . 【 补偿训练 】 化简： 　　 ，其中 θ∈(0 ， π). 【 解析 】 原式 = ① 当 θ∈ 时， ∈ ， cos ≥sin ， 此时原式 =sin +cos -cos +sin =2sin . ② 当 θ∈ 时， ∈ ， cos