高中数学第1章三角函数1_3_3函数y=Asinωxφ的图象优化训练苏教版必修4 7页

1.3.3 函数 y=Asin(ωx+φ)的图象 5 分钟训练（预习类训练，可用于课前） 1.函数 y=sin（-3x+ 4  ）的图象作适当变动就可以得到 y=sin（-3x）的图象，这种变动可 以是( ) A.沿 x 轴方向向右平移 4  个单位 B.沿 x 轴方向向左平移 4  个单位 C.沿 x 轴方向向右平移 12  个单位 D.沿 x 轴方向向左平移 12  个单位 思路解析：方法一（直接法）：由函数 y=sin（-3x+ 4  ）=sin［-3（x- 12  ）］的图象变换到 函数 y=sin（-3x）=sin［-3（x）］的图象，按照“左加右减”的原则，只需沿 x 轴方向向 左平移 12  个单位即可. 方法二（逆变换）：由函数 y=sin（-3x）=sin［-3（x）］的图象得到函数 y=sin（-3x+ 4  ） =sin［-3（x- 12  ）］的图象，需将原图沿 x 轴方向向右平移 12  个单位.所以反过来说，此问 题的答案应该是 D. 答案：D 2.如图 1-3-4 是周期为 2π的三角函数 y=f（x）的图象，那么 f（x）可以写成( ) 图 1-3-4 A.sin（1+x） B.sin（-1-x） C.sin（x-1） D.sin（1-x） 思路解析：“排除法”.根据所给图象经过点（1，0），排除选项 A、B，又当 x=0 时，y＞0， 所以排除 C 项，选 D 项. “直接法”.下图可以看作是由 y=sin（-x）=-sinx 的图象向右平移 1 个单位得到，所以所 求解析式为 y=sin［-（x-1）］=sin（1-x）.选 D 项. 答案：D 3.为了得到函数 y=sin（2x- 6  ）的图象，可以将函数 y=cos2x 的图象( ) A.向右平移 6  个单位长度 B.向右平移 3  个单位长度 C.向左平移 6  个单位长度 D.向左平移 3  个单位长度 思路解析：y=cos2x=sin（2x+ 2  ）=sin［2（x+ 3  ）- 6  ］. 答案：B 10 分钟训练（强化类训练，可用于课中） 1.(2004 辽宁)已知函数 f(x)=sin(πx- 2  )-1，则下列命题正确的是( ) A.f(x)是周期为 1 的奇函数 B.f(x)是周期为 2 的偶函数 C.f(x)是周期为 1 的非奇非偶函数 D.f(x)是周期为 2 的非奇非偶函数 思路解析：f(x)=sin(πx- 2  )-1=-cosπx-1,所以 T=2,且 f(x)=f(-x). 答案：D 2.(2004 全国卷Ⅱ)为了得到函数 y=sin(2x- 6  )的图象，可以将函数 y=cos2x 的图象 ( ) A.向右平移 6  个单位长度 B.向右平移 3  个单位长度 C.向左平移 6  个单位长度 D.向左平移 3  个单位长度 思路解析：∵y=sin(2x- 6  ) =cos[ 2  -(2x- 6  )] =cos( 3 2 -2x)=cos(2x- 3 2 ) =cos[2(x- 3  )], ∴将函数 y=cos2x 的图象向右平移 3  个单位长度. 答案：B 3.函数 y=3sin( 2 1 x+ 3  )的周期、振幅依次是( ) A．4π,3 B.4π,-3 C.π,3 D.π,-3 思路解析：考查 y=Asin(ωx+φ)(A>0,ω>0)的振幅和最小正周期的概念，以及最小正周期 的计算公式. 由 y=3sin( 2 1 x+ 3  )得振幅 A=3,周期 T=4π. 答案：A 4.已知函数 y=3sin（ 2 1 x- 4  ）. （1）用“五点法”作函数的图象； （2）说出此图象是由 y=sinx 的图象经过怎样的变化得到的； （3）求此函数的周期、振幅、初相. 思路解析：对于 y=Asin（ωx+φ）+h，应明确 A、ω决定“形变”，φ、h 决定“位变”，A 影响值域，ω影响周期，A、ω、φ影响单调性.当选用“先伸缩，后平移”的变化顺序时， 一定要注意针对 x 的变化，向左或向右平移 ||  个单位. 解：（1） （2）“先平移，后伸缩”. 先把 y=sinx 的图象上所有的点向右平移 4  个单位，得到 y=sin（x- 4  ）的图象；再把 y=sin （x- 4  ）图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），得到 y=sin（ 2 1 x- 4  ） 的图象；最后将 y=sin（ 2 1 x- 4  ）的图象上所有点的纵坐标伸长到原来的 3 倍（横坐标不 变），就得到 y=3sin（ 2 1 x- 4  ）的图象. (3)略. 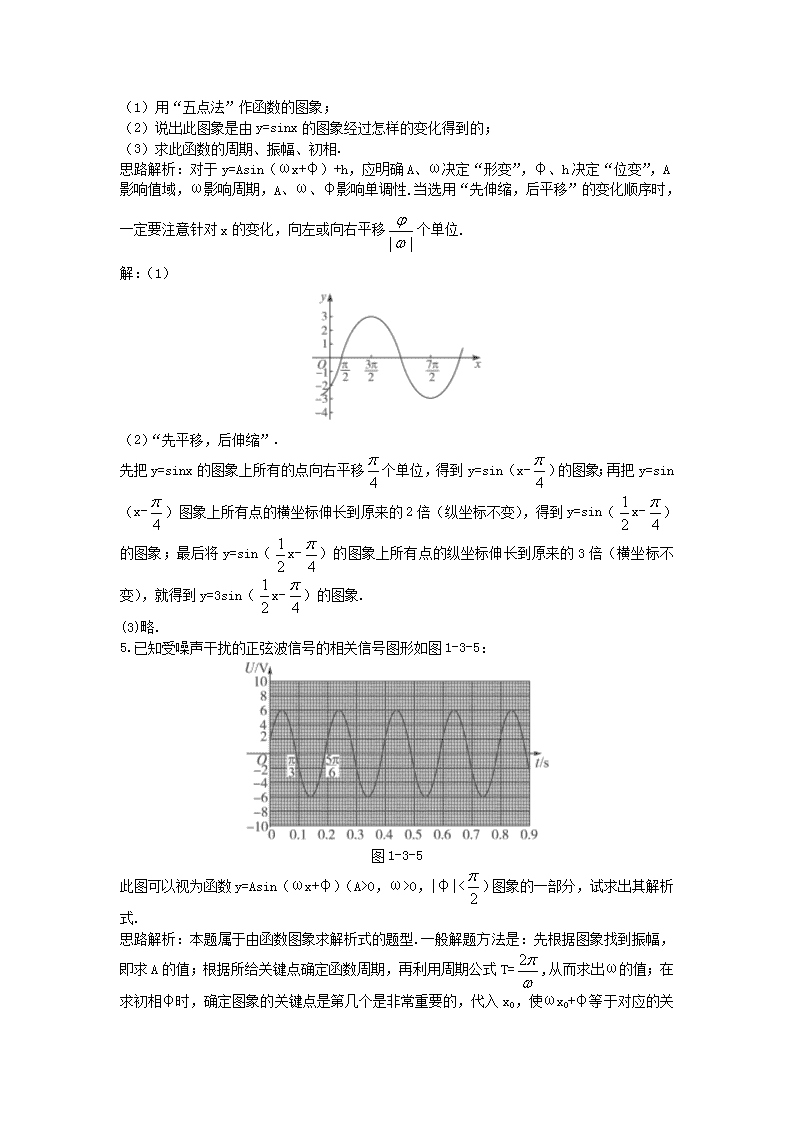5.已知受噪声干扰的正弦波信号的相关信号图形如图 1-3-5： 图 1-3-5 此图可以视为函数 y=Asin（ωx+φ）（A>0，ω>0，|φ|< 2  ）图象的一部分，试求出其解析 式. 思路解析：本题属于由函数图象求解析式的题型.一般解题方法是：先根据图象找到振幅， 即求 A 的值；根据所给关键点确定函数周期，再利用周期公式 T=  2 ,从而求出ω的值；在 求初相φ时，确定图象的关键点是第几个是非常重要的，代入 x0，使ωx0+φ等于对应的关 键点横坐标的值，如第一关键点对应 0，第二关键点对应 2  …… 解：已知信号最大、最小的波动幅度为 6 和-6，所以 A=6.又根据图象上相邻两点的坐标为 3  和 6 5 ，间距相当于 y=Asin（ωx+φ）的图象的半个周期，∴T=2（ 6 5 - 3  ）=π.∵T=  2 ， ∴T=  2 =π.解得ω=2.观察图象，点（ 3  ，0）是五个关键点中的第三个点，∴ 3  ×2+φ= π.解得φ= 3  .综上所述，y=6sin（2x+ 3  ）. 6.已知函数 y=Asin（ωx+φ）（A>0，ω>0，|φ|< 2  ）在一个周期内的简图（如图 1-3-6）. 求其相应的函数表达式，并说明它是由 y=sinx 经过怎样的变换得到的. 图 1-3-6 思路解析：应求出 A、ω、φ，观察图象易知振幅 A=2；周期 T= 12 11 -（- 12  ）=π=  2 ， 从而求得ω；对于φ，只需将点（- 12  ，0）代入解析式即可通过解方程获得.给出正弦函数 在一个周期内的图象，求它的解析式，常采用待定系数法.求解的一般步骤是： （1）设函数的解析式为 y=Asin（ωx+φ）+k； （2）观察图象的最高点与最低点，设其纵坐标分别为 M、m，则 A= 2 mM  ，k= 2 mM  ； （3）由始点与终点的横坐标 x0、x1，求周期即 T=x1-x0； （4）依公式ω= T 2 ，求出ω； （5）通过图象的平移或“五点法”作图的过程求φ. 解：因为 T= 12 11 -（- 12  ）=π=  2 ，所以ω=2.又易知 A=2，所以 y=2sin（2x+φ）.将点 （- 12  ，0）代入上式得 0=2sin［2×（- 12  ）+φ］，即 sin（φ- 6  ）=0.由|φ|< 2  得φ= 6  ， 所以 y=2sin（2x+ 6  ）. 它的图象可由 y=sinx 的图象作如下变换得到： y=sinx y=sin （ x+ 6  ） y=sin （ 2x+ 6  ） y=2sin（2x+ 6  ）. 志鸿教育乐园 耳误 一小伙子骑自行车为了装酷，把双后脱离了车把，路过岔路口时被交警看见。交警想让 这个小伙子双手掌握好方向，就冲他喊了一声：“手掌好！” 小伙子开始一愣，随后就扬了扬他的左手，对交警说：“同志们辛苦了！” 30 分钟训练（巩固类训练，可用于课后） 1.函数 y=sin(x+φ)(0≤φ≤π)是 R 上的偶函数，则φ等于( ) A.0 B. 4  C. 2  D.π 思路解析：把函数图象向左平移 2  个单位即可. 答案：C 2.(2005 天津)要得到 y= 2 cosx 的图象，只需将函数 y=2sin( 2 x+ 4  )的图象上所有点 的( ) A.横坐标缩短到原来的 2 1 倍（纵坐标不变）,再向左平行移动π个单位长度 B.横坐标缩短到原来的 2 1 倍（纵坐标不变），再向右平行移动π个单位长度 C.横坐标伸长到原来的 2 倍（纵坐标不变），再向左平行移动 4  个单位长度 D.横坐标伸长到原来的 2 倍（纵坐标不变），再向右平行移动 4  个单位长度 思路解析：y=cosx 的周期是 y= 2 sin(2x+ 4  )的周期的 2 倍，从周期的变化上知道横坐标 应该伸长.排除 A、B. y= 2 sin(2x+ 4  )的横坐标伸长 2 倍后变成了 y1= 2 sin(x+ 4  )，将 y= 2 cosx 化成正弦 形式为 y2= 2 sin(x+ 2  )，根据口诀“左加右减”得 y2 由 y1 向左移动 4  个单位得到的. 答案：C 3.(2005 福建)函数 y=sin(ωx+φ) (x∈R，ω>0，0≤φ<2π)的部分图象如图 1-3-7，则 ( ) 图 1-3-7 A.ω= 2  ,φ= 4  B.ω= 3  ,φ= 6  C.ω= 4  ,φ= 4  D.ω= 4  ,φ= 4 5 思路解析：由图易知 4 T ＝2，∴T=8. 而 T＝  2 =8，∴ω= 4  .排除 A、B. ∴函数 y=sin(ωx+φ)显然φ＝ 4  满足 sin( 4  ×1+ 4  )=1. 而φ＝ 4 5 ，则 sin( 4  ×1+ 4 5 )＝-1.排除 D. 答案：C 4.(2005 上海)函数 f(x)=sinx+2|sinx|,x∈［0,2π］的图象与直线 y=k 有且仅有两个不 同的交点，则 k 的取值范围是_______________. 思路解析：对于带有绝对值的函数，首先应该分区间分别写出解析式.画出图象，可以看出 有不同个交点时 k 的范围.f(x)=      ].2,[,sin ],,0[,sin3   xx xx 从图象可以看出直线 y=k 有且仅有两个不同的交点时 1