南通市2019届高三第三次调研测试数学 9页

南通市2019届高三第三次调研测试数学 结束 Y 输出y N ‎（第3题）‎ 开始 输入x y←3- x x≤1‎ y←3+x ‎1． 已知集合，，则 ▲ ．‎ ‎2． 已知复数（i是虚数单位）是纯虚数，则实数的值为 ▲ ．‎ ‎3． 右图是一个算法流程图．若输出的值为4，则输入x的值为 ▲ ．‎ ‎4． 已知一组数据6，6，9，，的平均数是，且，则该组数据的方差为 ▲ ．‎ ‎5． 一只口袋装有形状、大小都相同的4只小球，其中有3只白球，1只红球．从中1次随机摸出2只球，则2只球都是白球的概率为 ▲ ．‎ ‎6． 已知函数 则不等式的解集为 ▲ ．‎ ‎7． 已知是等比数列，前项和为．若，，则的值为 ▲ ．‎ ‎8． 在平面直角坐标系中，双曲线（）的右准线与两条渐近线分别交于A，B两点．若△AOB的面积为，则该双曲线的离心率为 ▲ ．‎ ‎9． 已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB=3 cm，BC=1 cm，CD=2 cm．将此直角梯形绕AB边所在的直线旋转一周，由此形成的几何体的体积为 ▲ cm3．‎ A B C D E F ‎（第11题）‎ A B C ‎6‎ ‎2‎ ‎3.5‎ ‎（第12题）‎ ‎10．在平面直角坐标系中，若曲线与在上交点的横坐标为，则的值为 ▲ ． ‎ ‎11．如图，正六边形中，若（），则的值为 ▲ ． ‎ ‎12．如图，有一壁画，最高点处离地面6 m，最低点处离地面3.5 m．若从离地高2 m的处观赏它，则离墙 ▲ m时，视角最大．‎ ‎13．已知函数，．若对任意，总存在，使得 9‎ 成立，则实数的值为 ▲ ．‎ ‎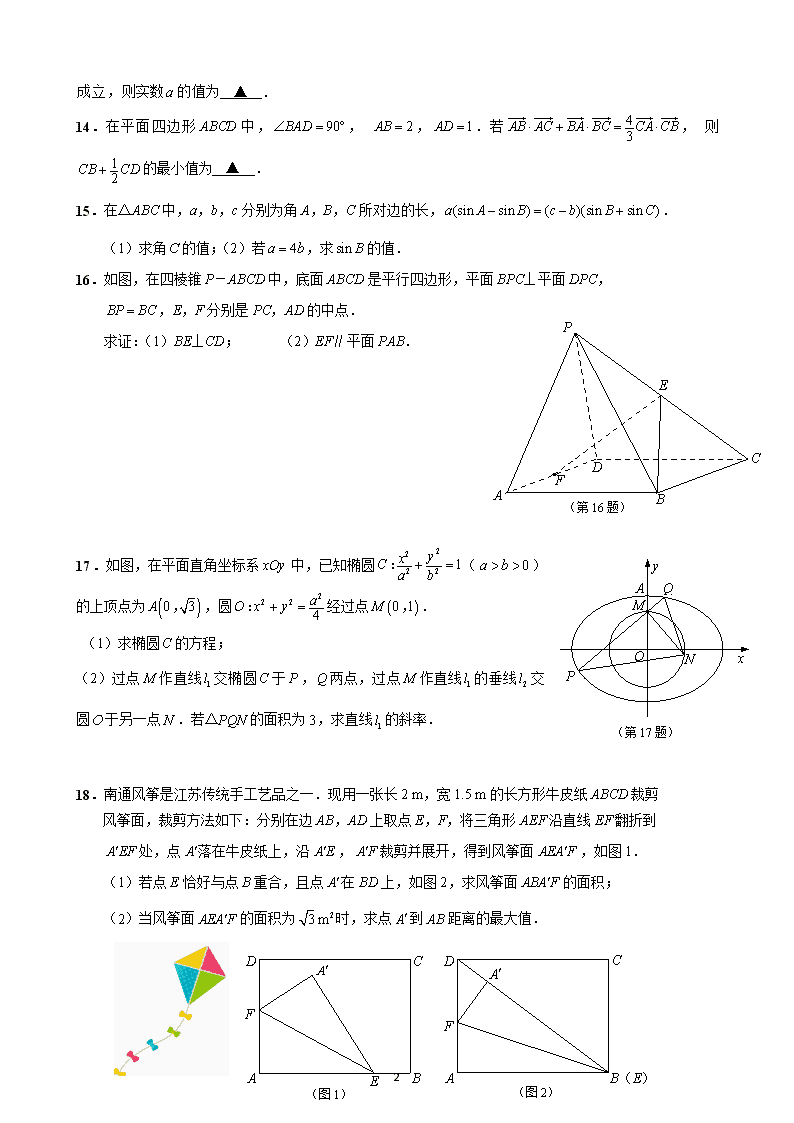14．在平面四边形ABCD中，， ，．若， 则的最小值为 ▲ ．‎ ‎15．在△ABC中，a，b，c分别为角A，B，C所对边的长，．‎ ‎（1）求角的值；（2）若，求的值．‎ A B C D P E F ‎（第16题）‎ ‎16．如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，平面BPC⊥平面DPC，‎ ‎，E，F分别是PC，AD的中点．‎ 求证：（1）BE⊥CD； （2）EF∥平面PAB．‎ x O A ‎（第17题）‎ y M N P Q ‎17．如图，在平面直角坐标系xOy中，已知椭圆（）的上顶点为，圆经过点．‎ ‎ （1）求椭圆的方程；‎ ‎（2）过点作直线交椭圆于，两点，过点作直线的垂线交圆于另一点．若△PQN的面积为3，求直线的斜率． ‎ ‎18．南通风筝是江苏传统手工艺品之一．现用一张长2 m，宽1.5 m的长方形牛皮纸ABCD裁剪 风筝面，裁剪方法如下：分别在边AB，AD上取点E，F，将三角形AEF沿直线EF翻折到 处，点落在牛皮纸上，沿，裁剪并展开，得到风筝面，如图1．‎ ‎（1）若点E恰好与点B重合，且点在BD上，如图2，求风筝面的面积；‎ ‎（2）当风筝面的面积为时，求点到AB距离的最大值．‎ ‎（图1）‎ A B C D F E ‎（图2）‎ A B（E）‎ C D F 9‎ ‎19．已知数列满足（），（）．‎ ‎（1）若，证明：是等比数列；‎ ‎（2）若存在，使得，，成等差数列．‎ ‎ ① 求数列的通项公式；‎ ‎ ② 证明：．‎ ‎20．已知函数（），是自然对数的底数．‎ ‎（1）当时，求的单调增区间；‎ ‎（2）若对任意的，（），求的最大值；‎ ‎（3）若的极大值为，求不等式的解集．‎ 9‎ ‎21．A．[选修4-2：矩阵与变换]‎ 已知，矩阵的逆矩阵．若曲线C在矩阵对应的变换作用下得到曲线，求曲线C的方程．‎ B．[选修4-4：坐标系与参数方程]‎ 在直角坐标平面内，以原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知点，‎ 的极坐标分别为，，曲线的方程为（）．‎ ‎（1）求直线的直角坐标方程；‎ ‎（2）若直线和曲线有且只有一个公共点，求的值．‎ C．[选修4-5：不等式选讲]‎ 已知，若关于的方程有实根，求的取值范围．‎ ‎22．现有一款智能学习APP，学习内容包含文章学习和视频学习两类，且这两类学习互不影响．‎ 已知该APP积分规则如下：每阅读一篇文章积1分，每日上限积5分；观看视频累计3分钟 积2分，每日上限积6分．经过抽样统计发现，文章学习积分的概率分布表如表1所示，视频 文章学习积分 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 概率 视频学习积分 ‎2‎ ‎4‎ ‎6‎ 概率 表1‎ 表2‎ 学习积分的概率分布表如表2所示．‎ ‎（1）现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；‎ ‎（2）现随机抽取3人了解学习情况，设积分不低于9分的人数为，求的概率分布及 数学期望．‎ ‎23．设，．‎ ‎（1）求的值；（2）化简．‎ 9‎ 南通市2019届高三第三次调研测参考答案 ‎1、 2、 3、 4、 5、 6、 ‎ ‎7、14 8、2 9、 10、 11、 12、 13、 14、‎ 15、 ‎（1）．（2）． ‎ ‎16、略 ‎17、（1）椭圆的方程为． （2）若的斜率为0，则，， 所以△PQN的面积为，不合题意，所以直线的斜率不为0． 设直线的方程为， 由消，得， 设，， 则，‎ 9‎ ‎， 所以． ‎ ‎ 直线的方程为，即，所以． 所以△PQN的面积，解得，即直线的斜率为． ‎ ‎18、（1）方法一：建立直角坐标系四边形的面积为．‎ 方法二：设，则．在直角△ABD中，， 所以，‎ A B C D F E x y 解得或（舍去）．所以． 所以△ABF的面积为，所以四边形的面积为．‎ ‎ （2）方法一：建立如图所示的直角坐标系． 设，，，则直线的方程为，因为点A，关于直线对称，所以解得． 因为四边形的面积为，所以， 所以． 因为，，以． 设，． ， 令，得或（舍去）． 列表如下：‎ ‎0‎ 单调递减 极小值 单调递增 ‎ ‎ ‎ 当时，取得极小值，即最小值， 所以的最大值为，此时点在CD上，，． 答：点到AB距离的最大值为． ‎ A B C D F E T 方法二：设，，则．因为四边形的面积为，所以，即，所以．过点作 9‎ AB的垂线，垂足为T，则 ．因为，，所以． （下同方法一）‎ ‎19、（1）由，得，得，即 ‎ ‎ 因为，所以，所以（），所以是以为首项，2为公比等比数列． ‎ ‎（2）① 设，由（1）知，， 所以，即，所以．因为，，成等差数列，则， 所以，所以，所以，即． ‎ ‎② 要证，即证，即证．设，则，且，从而只需证，当时，． 设（），则，所以在上单调递增，所以，即，因为，所以，所以，原不等式得证．‎ ‎20、（1）的定义域为． 由， 令，因为，得， 因为，的单调增区间是．‎ ‎（2）当时，，不合题意； 当时，令，得或， 所以在区间和上单调递减． 因为，且在区间上单调递增，所以在处取极小值，即最小值为． 若，，则，即．不妨设，则． 设（），则．当时，；当时，，所以在上单调递增；在上单调递减，所以，即，所以的最大值为． ‎ ‎ （3）由（2）知，当时，无极大值， 当时，在和 9‎ 上单调递增；在上单调递减，所以在处取极大值， 所以，即． 设，即， 当，，所以； 当，， 由（2）知，，又， 所以，且不恒为零， 所以在上单调递增．不等式，即为，所以， 即不等式的解集为． ‎ ‎21A、由题意得，，即， 所以，即矩阵． 设为曲线C上的任意一点，在矩阵对应的变换作用下变为点， 则 ，即 由已知条件可知，满足，整理得：， 所以曲线C的方程为．21B、（1）分别将，转化为直角坐标为，， 所以直线的直角坐标方程为． ‎ ‎ （2）曲线C的方程为（），其直角坐标方程为 又直线AB和曲线C有且只有一个公共点，即直线与圆相切， 所以圆心到直线AB的距离为，即的值为． ‎ ‎21C、因为关于的方程有实根， 所以，即 当时，，得； 当时，14，恒成立，即； 当时，，得， 综上：所求的取值范围为． ‎ ‎22、（1）由题意，获得的积分不低于9分的情形有：‎ 文章 ‎3‎ ‎4‎ ‎5‎ ‎5‎ 视频 ‎6‎ ‎6‎ ‎4‎ ‎6‎ 因为两类学习互不影响，所以概率，所以每日学习积分不低于9分的概率为． ‎ 9‎ ‎（2）随机变量的所有可能取值为0，1，2，3．由（1）每个人积分不低于9分的概率为．‎ ‎；；；．‎ 所以，随机变量的概率分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以．所以，随机变量的数学期望为．‎ ‎23、（1）由，，所以． ‎ ‎（2）设，则 ‎ ① 因为，‎ 所以 ②‎ ‎ ①+②得，，即，所以． ‎ 9‎