2020_2021学年新教材高中数学第六章平面向量及其应用6 42页

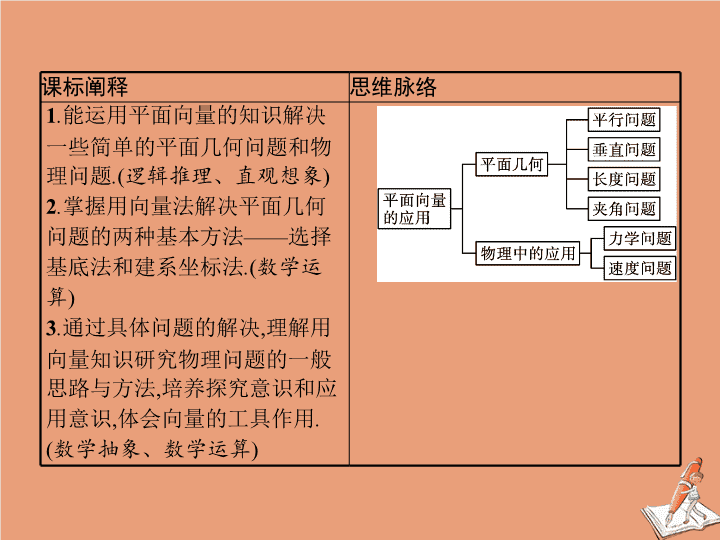
6 . 4 . 1 　 平面几何中的向量方法 6 . 4 . 2 　 向量在物理中的应用举例 课标阐释 思维脉络 1 . 能运用平面向量的知识解决一些简单的平面几何问题和物理问题 . ( 逻辑推理、直观想象 ) 2 . 掌握用向量法解决平面几何问题的两种基本方法 —— 选择基底法和建系坐标法 . ( 数学运算 ) 3 . 通过具体问题的解决 , 理解用向量知识研究物理问题的一般思路与方法 , 培养探究意识和应用意识 , 体会向量的工具作用 . ( 数学抽象、数学运算 ) 激趣诱思 知识点拨 英国科学家赫胥黎应邀到都柏林演讲 , 由于时间紧迫 , 他一跳上出租车 , 就急着说 :“ 快 ! 快 ! 来不及了 !” 司机遵照指示 , 猛开了好几分钟 , 赫胥黎才发现不太对劲 , 问道 :“ 我没有说要去哪里吗 ?” 司机回答 :“ 没有啊 ! 你只叫我快开啊 !” 赫胥黎于是说 :“ 对不起 , 请掉头 , 我要去都柏林 . ” 由此可见 , 速度不仅有大小 , 而且有方向 . 在我们的生活中 , 有太多的事物不仅与表示它的量的大小有关 , 而且也与方向有关 . 激趣诱思 知识点拨 知识点一、向量在平面几何中的应用 1 . 由于向量的线性运算和数量积运算具有鲜明的几何背景 , 平面几何图形的许多性质 , 如全等、相似、长度、夹角等都可以由向量的 线性运算 及 数量积 表示出来 , 因此平面几何中的许多问题都可用向量运算的方法加以解决 . 2 . 用向量方法解决平面几何问题的 “ 三步曲 ”, 即 (1) 建立平面几何与向量的联系 , 用 向量 表示问题中涉及的几何元素 , 将平面几何问题转化为 向量 问题 ; (2) 通过 向量 运算 , 研究几何元素之间的关系 , 如距离、夹角等问题 ; (3) 把 运算结果 “ 翻译 ” 成几何关系 . 3 . 平行四边形两条对角线长的平方和等于两条邻边长的平方和的两倍 . 这一结论 , 可以用向量表示为 : ( a + b ) 2 + ( a - b ) 2 = 2( a 2 + b 2 ) . 激趣诱思 知识点拨 微练习 (1) 已知 A (1,2), B (2,3), C ( - 2,5), 则 △ ABC 的形状是 ( 　　 ) A. 直角三角形 　　　　 B. 锐角三角形 C. 钝角三角形 D . 等边三角形 (2) 在平面直角坐标系 xOy 中 , 已知点 A ( - 1, - 2), B (2,3), C ( - 2, - 1), 以线段 AB , AC 为邻边的平行四边形的两条对角线的长分别是 　　　　　 , 　　　　　 .  激趣诱思 知识点拨 激趣诱思 知识点拨 知识 点二、向量在物理中的应用 1 . 物理学中的许多量 , 如力、速度、加速度、位移都是 向量 . 2 . 物理学中的力、速度、加速度、位移的合成与分解就是向量的加减法 . 3 . 利用向量方法解决物理问题的基本步骤 : (1) 问题转化 , 即把物理问题转化为数学问题 ; (2) 建立模型 , 即建立以向量为载体的数学模型 ; (3) 求解参数 , 即求向量的模、夹角、数量积等 ; (4) 回答问题 , 即把所得的数学结论回归到物理问题 . 激趣诱思 知识点拨 微练习 (1) 已知三个力 F 1 = ( - 2, - 1), F 2 = ( - 3,2), F 3 = (4, - 3) 同时作用于某物体上一点 , 为使物体保持平衡 , 现加上一个力 F 4 , 则 F 4 等于 ( 　　 ) A.( - 1, - 2) 　　　 B.(1, - 2) 　　　 C.( - 1,2) 　　　 D.(1,2) (2) 已知速度 v 1 , v 2 的大小分别为 | v 1 |= 10 m/s, | v 2 |= 12 m/s, 且 v 1 与 v 2 的夹角为 60°, 则 v 1 与 v 2 的合速度 v 的大小是 ( 　　 ) A.2 m/s B.10 m/s C.12 m/s D.2 m/s 激趣诱思 知识点拨 解析 : (1) 由已知 F 1 + F 2 + F 3 + F 4 = 0 , 故 F 4 =- ( F 1 + F 2 + F 3 ) =- [( - 2, - 1) + ( - 3,2) + (4, - 3)] =- ( - 1, - 2) = (1,2) . (2) ∵ | v | 2 =| v 1 + v 2 | 2 =| v 1 | 2 + 2 v 1 · v 2 +| v 2 | 2 = 100 + 2 × 10 × 12cos 60° + 144 = 364, ∴ | v |= 2 (m/s ) . 答案 : (1)D 　 (2)D 探究一 探究二 素养形成 当堂检测 向量在平面几何中的应用 角度 1 　 平行或共线问题 探究一 探究二 素养形成 当堂检测 反思感悟 证明 A , B , C 三点共线的步骤 (1) 证明其中两点组成的向量与另外两点组成的向量共线 . (2) 说明两向量有公共点 . (3) 下结论 , 即 A , B , C 三点共线 . 探究一 探究二 素养形成 当堂检测 变式训练 1 如图 , 已知 AD , BE , CF 是 △ ABC 的三条高 , 且交于点 O , DG ⊥ BE 于 G , DH ⊥ CF 于 H. 求证 : HG ∥ EF. 探究一 探究二 素养形成 当堂检测 角度 2 　 垂直问题 例 2 如图 , 在正方形 ABCD 中 , P 是对角线 BD 上的一点 , 四边形 PECF 是矩形 , 用向量证明 : PA ⊥ EF. 探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 ( 方法二 ) 以 D 为原点 , DC , DA 所在直线分别为 x 轴、 y 轴 , 建立如图所示的平面直角坐标系 . 设正方形边长为 a , 由于 P 是对角线 BD 上的一点 , 设 DP= λ DB= λ a (0 < λ < 1 ), 则 A (0, a ), P ( λ a , λ a ), E ( a , λ a ), F ( λ a ,0 ), 探究一 探究二 素养形成 当堂检测 反思感悟 向量法证明平面几何中 AB ⊥ CD 的 方法 探究一 探究二 素养形成 当堂检测 变式训练 2 如图所示 , 在正方形 ABCD 中 , E , F 分别是 AB , BC 的中点 , 求证 : AF ⊥ DE. 探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 角度 3 　 长度问题 例 3 如图 , 在平行四边形 ABCD 中 , 已知 AD= 1, AB= 2, 对角线 BD= 2, 求对角线 AC 的长 . 分析 本题是求线段长度的问题 , 可以转化为求向量的模来解决 . 探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 变式训练 3 已知 △ ABC , ∠ BAC= 60°, AB= 2, AC= 3, 则 BC 的长为 ( 　　 ) 答案 : B 探究一 探究二 素养形成 当堂检测 角度 4 　 夹角问题 例 4 已知矩形 ABCD , AB = , AD= 1, E 为 DC 上靠近 D 的三等分点 , 求 ∠ EAC 的大小 . 分析 可建立平面直角坐标系 , 通过坐标运算运用夹角公式求解 . 探究一 探究二 素养形成 当堂检测 反思感悟 平面几何中夹角问题的求解策略 利用平面向量解决几何中的夹角问题时 , 本质是将平面图形中的角视为两个向量的夹角 , 借助夹角公式进行求解 , 这类问题也有两种方向 , 一是利用基底法 , 二是利用坐标运算 . 在求解过程中 , 务必注意向量的方向 . 探究一 探究二 素养形成 当堂检测 延伸探究 本例中 , 条件不变 , 试问 : 在 BC 上是否存在点 M , 使得 ∠ EAM= 45°? 若存在 , 求出点 M 的位置 ; 若不存在 , 说明理由 . 探究一 探究二 素养形成 当堂检测 向量在物理中的应用 角度 1 　 用向量解决力学问题 例 5 如图所示 , 在细绳 O 处用水平力 F 2 缓慢拉起所受重力为 G 的物体 , 绳子与铅垂方向的夹角为 θ , 绳子所受到的拉力为 F 1 . (1) 求 | F 1 | , | F 2 | 随 θ 角的变化而变化的情况 ; (2) 当 | F 1 | ≤2 | G | 时 , 求 θ 角的取值范围 . 探究一 探究二 素养形成 当堂检测 反思感悟 力的合成与分解的向量解法 运用向量解决力的合成与分解时 , 实质就是向量的线性运算 , 因此可借助向量运算的平行四边形法则或三角形法则进行求解 . 探究一 探究二 素养形成 当堂检测 变式训练 4 一个物体受到平面上的三个力 F 1 , F 2 , F 3 的作用处于平衡状态 , 已知 F 1 , F 2 成 60° 角 , 且 | F 1 |= 3 N, | F 2 |= 4 N, 则 F 1 与 F 3 夹角的余弦值是 　 .  探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 角度 2 　 用向量解决速度问题 例 6 在风速 为 km/h 的西风中 , 飞机以 150 km/h 的航速向西北方向飞行 , 求没有风时飞机的航速和航向 . 分析 解本题首先根据题意作图 , 再把物理问题转化为向量的有关运算求解 . 探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 反思感悟 速度问题的向量解法 运用向量解决物理中的速度问题时 , 一般涉及速度的合成与分解 , 因此应充分利用三角形法则与平行四边形法则将物理问题转化为数学中的向量问题 , 正确地作出图形解决问题 . 探究一 探究二 素养形成 当堂检测 变式训练 5 一船以 8 km/h 的速度向东航行 , 船上的人测得风自北方来 ; 若船速加倍 , 则测得风自东北方向来 , 求风速的大小及方向 . 解 : 分别取正东、正北方向上的单位向量 i , j 为基底 , 设风速为 x i +y j . 依题意第一次船速为 8 i , 第二次船速为 16 i . 探究一 探究二 素养形成 当堂检测 物理学中力的向量解法 典例 (1) 一物体在力 F 1 = (3, - 4), F 2 = (2, - 5), F 3 = (3,1) 的共同作用下从点 A (1,1) 移动到点 B (0,5) . 在这个过程中三个力的合力所做的功等于 　　　　　 .  (2) 设作用于同一点的三个力 F 1 , F 2 , F 3 处于平衡状态 , 若 | F 1 |= 1, | F 2 |= 2, 且 F 1 与 F 2 的夹角 为 π , 如图所示 . ① 求 F 3 的大小 ; ② 求 F 2 与 F 3 的夹角 . 探究一 探究二 素养形成 当堂检测 (1) 解析 : 因为 F 1 = (3, - 4), F 2 = (2, - 5), F 3 = (3,1), 所以合力 F = F 1 + F 2 + F 3 = (8, - 8 ), = ( - 1,4), 则 F · =- 1 × 8 - 8 × 4 =- 40, 即三个力的合力所做的功为 - 40 . 答案 : - 40 探究一 探究二 素养形成 当堂检测 探究一 探究二 素养形成 当堂检测 方法点睛向量在物理中的应用 (1) 求力向量 , 速度向量常用的方法 : 一般是向量几何化 , 借助于向量求和的平行四边形法则求解 . (2) 用向量方法解决物理问题的步骤 : ① 把物理问题中的相关量用向量表示 ; ② 转化为向量问题的模型 , 通过向量运算使问题解决 ; ③ 结果还原为物理问题 . 探究一 探究二 素养形成 当堂检测 答案 : D 探究一 探究二 素养形成 当堂检测 答案 : ( - 3,1) 或 ( - 1, - 3 ) 探究一 探究二 素养形成 当堂检测 3 . 如图 , 在矩形 ABCD 中 , AB = , BC= 3, BE ⊥ AC , 垂足为 E , 则 ED= 　　　　　 .  探究一 探究二 素养形成 当堂检测 解析 : 如图 , 以 A 为坐标原点 , AD , AB 所在直线分别为 x 轴 , y 轴建立平面直角坐标系 , 探究一 探究二 素养形成 当堂检测 4 . 在平行四边形 ABCD 的对角线 BD 的延长线及反向延长线上 , 取点 F , E , 使 BE=DF ( 如图 ) . 用向量的方法证明四边形 AECF 也是平行四边形 . 探究一 探究二 素养形成 当堂检测 5 . 在长江南岸某渡口处 , 江水以 12 . 5 km/h 的速度向东流 , 渡船在静水中的速度为 25 km/h . 渡船要垂直地渡过长江 , 其航向应如何确定 ?