安徽省太和中学2019-2020学年高二下学期开学考试数学（理）试题 Word版含答案 13页

太和中学2019～2020学年度高二下学期开学考试 数学试题（理科）‎ 考生注意：‎ ‎1．本试卷分选择题和非选择题两部分．满分150分，考试时间120分钟．‎ ‎2．答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚．‎ ‎3．考生作答时，请将答案答在答题卡上．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．‎ ‎4．本卷命题范围：北师大版必修3（30%），选修2-1（5%），选修2-2第一章、选修4-5（15%）．‎ 一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．命题“，”的否定是（ ）‎ A． B．‎ C． D．‎ ‎2．双曲线的渐近线方程为（ ）‎ A． B． C． D．‎ ‎3．已知某团队有老年人28人，中年人56人，青年人84人，若按老年人，中年人，青年人用分层抽样的方法从中抽取一个容量为12的样本，则从中年人中应抽取（ ）‎ A．2人 B．3人 C．5人 D．4人 ‎4．椭圆的焦点在y轴上，长轴长是短轴长的两倍，则m的值为（ ）‎ A． B． C． D．4‎ ‎5．已知拋物线的焦点为F，点 是抛物线C上三个不同的点，若，则有（ ）‎ A． B． C． D．‎ ‎6．在区间上任取一个数x，若x满足的概率为，则实数m的值为（ ）‎ A．5 B．6 C．7 D．8‎ ‎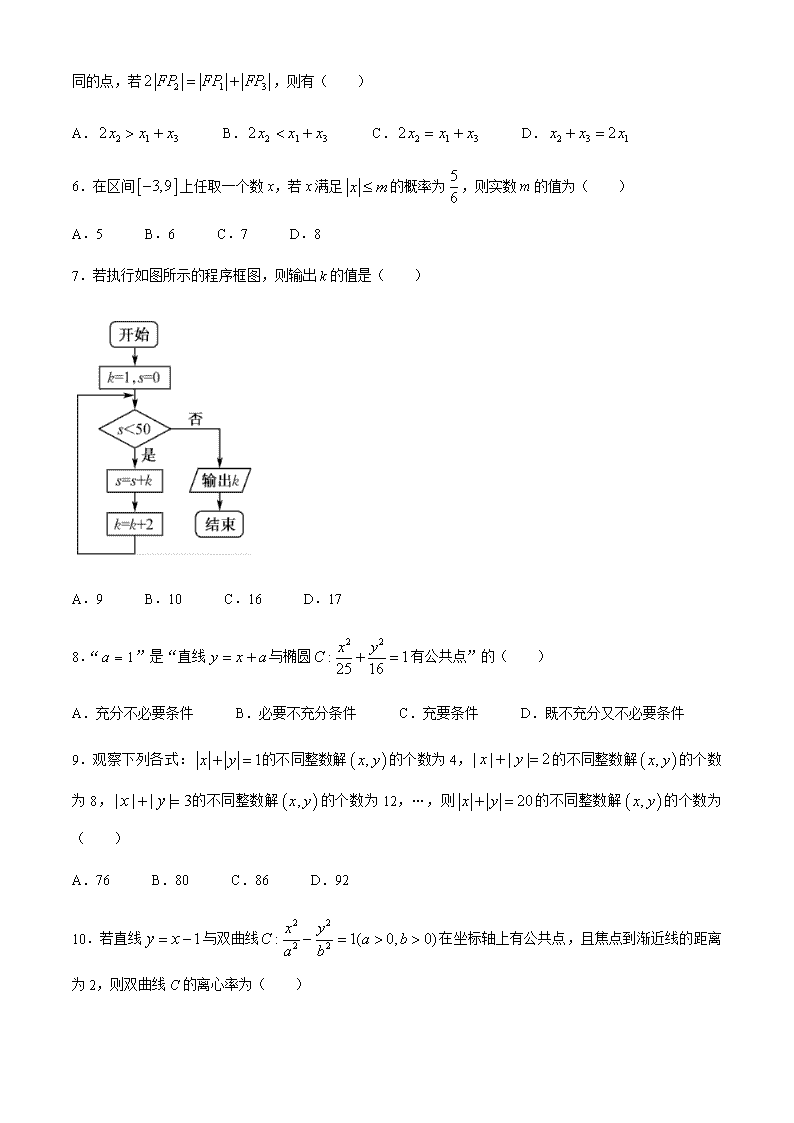7．若执行如图所示的程序框图，则输出k的值是（ ）‎ A．9 B．10 C．16 D．17‎ ‎8．“”是“直线与椭圆有公共点”的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分又不必要条件 ‎9．观察下列各式：的不同整数解的个数为4，的不同整数解的个数为8，的不同整数解的个数为12，…，则的不同整数解的个数为（ ）‎ A．76 B．80 C．86 D．92‎ ‎10．若直线与双曲线在坐标轴上有公共点，且焦点到渐近线的距离为2，则双曲线C的离心率为（ ）‎ A． B． C． D．5‎ ‎11．某学校举办科技节活动，有甲、乙、丙、丁四个团队参加“智能机器人”项目比赛，该项目只设置一个一等奖，在评奖揭晓前，小张、小王、小李、小赵四位同学对这四个参赛团队获奖结果预测如下：‎ 小张说：“甲或乙团队获得一等奖”；‎ 小王说：“丁团队获得一等奖”；‎ 小李说：“乙、丙两个团队均未获得一等奖”；‎ 小赵说：“甲团队获得一等奖”．‎ 若这四位同学中只有两位预测结果是对的，则获得一等奖的团队是（ ）‎ A．甲 B．乙 C．丙 D．丁 ‎12．过抛物线焦点F的直线l与抛物线相交于A，B两点，若以线段为直径的圆与直线相切，则直线l的方程为（ ）‎ A．或 B．或 C．或 D．或 二、填空题：本题共4小题，每小题5分，共20分．‎ ‎13．某电子商务公司对10000名网络购物者2017年度的消费情况进行统计，发现消费金额（单位：万元）都在区间内，其频率分布直方图如下图，则直方图中实数a的值是__________．‎ ‎14．若“”是“”的充分不必要条件，则实数m的取值范围是_________．‎ ‎15．在正方体中，点E是线段的中点，则直线与所成角的余弦值是_______．‎ ‎16．已知直线与椭圆交于A，B两点，若椭圆上存在一点P使得面积最大，则点P的坐标为__________．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分10分）‎ 已知函数．‎ ‎（1）求不等式的解集；‎ ‎（2）若关于x的不等式的解集非空，求m的取值范围．‎ ‎18．（本小题满分12分）‎ 某种设备随着使用年限的增加，每年的维护费相应增加．现对一批该设备进行调査，得到这批设备自购入使用之日起前五年设备每年每台的平均维护费用如下表：‎ 前x（年）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 维护费y（万元）‎ ‎1.1‎ ‎1.5‎ ‎1.8‎ ‎2.2‎ ‎2.4‎ ‎（1）若维护费y（万元）与年份x（年）之间存在线性相关关系，试求y关于x的线性回归方程；‎ ‎（2）据（1）求解估计这批设备自购入使用之日起前8年每台的平均维护费用．‎ 注，‎ ‎，‎ ‎．‎ ‎19．（本小题满分12分）‎ 如图，已知直线l经过抛物线的焦点F，且与抛物线相交于A，B两点．‎ ‎（1）若，求点A的坐标；‎ ‎（2）求线段长度的最小值．‎ ‎20．（本小题满分12分）‎ 某高级中学今年高一年级招收学生720人，学校为使这些学生尽快适应高中学习将这720人分为三个批次进行相关培训，在这三个批次的学生中男、女学生人数如下表：‎ 第一批次 第二批次 第三批次 女 m n ‎72‎ 男 ‎180‎ ‎132‎ k 已知在这720名学生中随机抽取1名，抽到第一批次、第二批次中女学生的概率分别是0.25，0.15．‎ ‎（1）求m，n，k的值；‎ ‎（2）为了检验培训的效果，现从三个批次中按分层抽样的方法抽取6名同学问卷调查，求三个批次被选取的人数分别是多少？‎ ‎（3若从第（2）小问选取的学生中随机选出两名学生进行访谈，求“参加访谈的两名同学至少有一个人来自第一个批次”的概率．‎ ‎21．（本小题满分12分）‎ 如图，在三棱台中，D，E分别是，的中点，平面，是等边三角形，．‎ ‎（1）证明：平面；‎ ‎（2）求二面角的正弦值．‎ ‎22．（本小题满分12分）‎ 已知圆恰好经过椭圆的两个焦点和两个顶点．‎ ‎（1）求椭圆C的方程；‎ ‎（2）经过原点的直线l（不与坐标轴重合）交椭圆C于A，B两点，轴，垂足为M，连接并延长交椭圆C于N，证明：以线段为直径的圆经过点A．‎ 太和中学2019～2020学年度高二下学期开学考试·数学试题（理科）‎ 参考答案、提示及评分细则 ‎1．C 特称命题的否定是全称命题．‎ ‎2．B 根据题意可得，，所以双曲线的渐近线方程为．故选B．‎ ‎3．D 据题设知，从中年人中应抽取4人．故选D．‎ ‎4．A 由题意，且，∴．故选A．‎ ‎5．C ∵，∴，∴．故选C．‎ ‎6．C 区间的长度为12，由得，对应区间长度为，若，概率为，不合题意，所以，所以概率为，所以．故选C．‎ ‎7．D ，，；，，；，，；，，；，，；，，；，，；，，；，，此时，循环结束，输出k的值为17．‎ ‎8．A 由，得直线过点．又点在椭圆内部，故直线与椭圆有公共点，而直线与椭圆有公共点不一定．故选A．‎ ‎9．B 观察可得不同整数解的个数4，8，12，……，可以构成一个首项为4，公差为4的等差数列，通项公式为，则的不同整数解的个数为第20项，∴，故选B．‎ ‎10．A 设双曲线的半焦距为c，由条件知，，焦点到渐近线的距离为，所以．故选A．‎ ‎11．D 若甲获得一等奖，则小张、小李、小赵的预测都正确，与题意不符；若乙获得一等奖，则只有小张的预测正确，与题意不符；若丙获得一等奖，则四人的预测都错误，与题意不符；若丁获得一等奖，则小王、小李的预测正确，小张、小赵的预测错误，符合题意，故选D．‎ ‎12．B 当直线l垂直与x轴时，解得，以为直径的圆为与直线 相离，故直线不满足题意；当直线l的斜率存在时，设，直线l的方程为，则化简得．圆的半径为，圆心到直线的距离为，解得，故直线l的方程为或．故选B．‎ 另解：过A，B分别作准线的垂线．垂足分别为，，则，所以以为直径的圆与直线相切，又以为直径的圆与相切，故圆的直径为17，所以．设直线与抛物线联立得．记，则，∴．又．∴．故选B．‎ ‎13．3.0 据题意，得，解得．‎ ‎14． 设，由题意可得，，即，∴m的取值范围是．‎ ‎15． 以D为原点，，分别为x，y，z轴建立空间直角坐标系，设正方体边长为1，则，‎ ‎．‎ ‎16． 由题意可得弦长为定值，要使面积最大，则只要点P到直线的距离最大，当平行于直线l的直线与椭圆相切时，对应的切点到直线l的距离最大或最小．设直线 ‎，直线与椭圆联立得化简得，则，解得．当时，直线与直线l的距离为．当时，直线与直线l的距离为．∴当时，，解得，代入直线解得，即点P的为坐标．‎ ‎17．解：（1） 1分 当时，无解； 2分 当时，由，得； 3分 当时，恒成立． 4分 所以的解集为． 5分 ‎（2）由有解，得有解， 6分 而， 7分 所以，， 8分 解得． 9分 所以m的取值范围是． 10分 ‎18．解：（1）， 1分 ‎， 2分 ‎， 3分 ‎， 4分 所以， 6分 ‎， 7分 所以所求回归方程为． 8分 ‎（2）据（1）求解知，‎ 所以当时，（万元）．‎ 即据（1）求解估计这批设备自购入使用之日起前8年每年每台平均维护费用为3.45万元． 12分 ‎19．解：（1）由，得，其准线方程为，焦点，设．‎ 由抛物线的定义可知，，从而．代入，解得．‎ ‎∴点A的坐标为或． 6分 ‎（2）当直线l的斜率存在时，‎ 设直线l的方程为．‎ 与抛物线方程联立，得 消去y整理得，．‎ ‎∵直线与抛物线相交于A，B两点，‎ 则，并设其两根为，‎ ‎∴．‎ 由抛物线的定义可知，．当直线l的斜率不存在时，直线l的方程为，与抛物线相交于，此时，‎ ‎∴，即线段长度的最小值为4． 12分 ‎20．解：（1）． 3分 ‎（2）由题意知，第一批次、第二批次、第三批次的人数分别是360，240，120．‎ ‎，‎ 所以第一批次、第二批次、第三批次被抽取的人数分别为3，2，1． 6分 ‎（3）第一批次选取的三个学生设为，第二批次选取的学生为，第三批次选取的学生为C，则这6名学员中随机选出两名学员的所有基本事件为，，，，，，，，，，，，，，共15个， 8分 ‎“两名同学至少有一个来自第一个批次”的事件包括，，，，，，，，，，，共12个， 10分 所以“两名同学至少有一个来自第一个批次”的概率． 12分 ‎21．解：（1）证明：因为，D为棱的中点，‎ 所以，‎ 所以四边形为平行四边形，从而． 1分 又平面平面，‎ 所以平面． 2分 因为是的中位线，所以，‎ 同理可证，平面． 3分 因为，所以平面平面． 4分 又平面，所以平面． 5分 ‎（2）以所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，‎ 设，则，则． 6分 设平面的一个法向量，则 即 取，得． 8分 同理，设平面的一个法向量，‎ 又，‎ 由，得 取，得． 10分 所以，‎ 即二面角的正弦值为． 12分 ‎22．（1）解：由题意可知，，‎ 所以椭圆C的方程为． 3分 ‎（2）证明：设直线l的斜率为，则直线l的方程为，．‎ 直线的斜率为，所以直线的方程为， 5分 联立得， 6分 记B，N的横坐标分别为，由韦达定理知：，‎ 所以，于是， 8分 所以直线的斜率为， 10分 因为，所以，‎ 所以以线段为直径的圆一定经过点A． 12分