高考数学专题复习练习：单元质检五 5页

单元质检五　平面向量、数系的扩充与复数的引入 ‎(时间:45分钟　满分:100分)‎ ‎　单元质检卷第13页　 ‎ 一、选择题(本大题共12小题,每小题6分,共72分)‎ ‎1.(2016河南郑州三模)设复数i-2‎‎1+i=a+bi(a,b∈R),则a+b=(　　)‎ ‎　　　　　　　　　　　　　　　　　　　‎ A.1 B.2 C.-1 D.-2‎ 答案A 解析∵i-2‎‎1+i=-‎1‎‎2‎‎+‎‎3‎‎2‎i=a+bi,‎ ‎∴a=-‎1‎‎2‎,b=‎3‎‎2‎.∴a+b=1,故选A.‎ ‎2.已知O是△ABC所在平面内一点,D为BC边的中点,且2OA‎+OB+‎OC=0,则有(　　)‎ A.AO=2OD B.‎AO‎=‎OD C.AO=3OD D.2‎AO‎=‎OD 答案B 解析由2OA‎+OB+‎OC=0,得OB‎+‎OC=-2OA=2AO,即OB‎+‎OC=2OD=2AO,所以OD‎=‎AO,故选B.‎ ‎3.(2016河南商丘三模)设向量e1,e2是两个互相垂直的单位向量,且a=2e1-e2,b=e2,则|a+2b|=(　　)‎ A.2‎2‎ B.‎5‎ C.2 D.4‎ 答案B 解析∵向量e1,e2是两个互相垂直的单位向量,‎ ‎∴|e1|=1,|e2|=1,e1·e2=0.‎ ‎∵a=2e1-e2,b=e2,∴a+2b=2e1+e2.‎ ‎∴|a+2b|2=4e‎1‎‎2‎+4e1·e2+e‎2‎‎2‎=5.‎ ‎∴|a+2b|=‎5‎.故选B.‎ ‎4.已知菱形ABCD的边长为a,∠ABC=60°,则BD‎·‎CD=(　　)‎ A.-‎3‎‎2‎a2 B.-‎3‎‎4‎a2 C.‎3‎‎4‎a2 D.‎3‎‎2‎a2‎ 答案D 解析如图,设BA=a,BC=b.‎ 则BD‎·‎CD=(BA‎+‎BC)·BA=(a+b)·a=a2+a·b=a2+a·a·cos 60°=a2+‎1‎‎2‎a2=‎3‎‎2‎a2.‎ ‎5.(2016山西太原三模)已知复数z=‎5+3i‎1-i,则下列说法正确的是(　　)‎ A.z的虚部为4i B.z的共轭复数为1-4i C.|z|=5‎ D.z在复平面内对应的点在第二象限 答案B 解析∵z=‎5+3i‎1-i‎=‎(5+3i)(1+i)‎‎(1-i)(1+i)‎=‎‎2+8i‎2‎=1+4i,‎ ‎∴z的共轭复数为1-4i.故选B.‎ ‎6.已知向量OA=(2,2),OB=(4,1),在x轴上存在一点P使AP‎·‎BP有最小值,则P点的坐标是(　　)‎ A.(-3,0) B.(2,0) C.(3,0) D.(4,0)‎ 答案C 解析设P点坐标为(x,0),则AP=(x-2,-2),BP=(x-4,-1).‎ AP‎·‎BP‎=(x-2)(x-4)+(-2)×(-1)=x2-6x+10=(x-3)2+1.‎ 当x=3时,AP‎·‎BP有最小值1.∴点P坐标为(3,0).‎ ‎7.已知向量a=(1,2),b=(1,0),c=(3,4),若λ为实数,(b+λa)⊥c,则λ的值为(　　)‎ A.-‎3‎‎11‎ B.-‎11‎‎3‎ C.‎1‎‎2‎ D.‎‎3‎‎5‎ 答案A 解析b+λa=(1,0)+λ(1,2)=(1+λ,2λ),c=(3,4),‎ 又(b+λa)⊥c,∴(b+λa)·c=0,即(1+λ,2λ)·(3,4)=3+3λ+8λ=0,解得λ=-‎3‎‎11‎,故选A.‎ ‎8.已知点A(-1,1),B(1,2),C(-2,-1),D(3,4),则向量AB在CD方向上的投影为(　　)‎ A.‎3‎‎2‎‎2‎ B.‎3‎‎15‎‎2‎ C.-‎3‎‎2‎‎2‎ D.-‎‎3‎‎15‎‎2‎ 答案A 解析AB=(2,1),CD=(5,5),向量AB在CD上的投影为AB‎·‎CD‎|CD|‎‎=‎15‎‎5‎‎2‎=‎‎3‎‎2‎‎2‎,故选A.‎ ‎9.(2016山东师大附中模拟)设ak=coskπ‎6‎,sinkπ‎6‎+coskπ‎6‎,k∈Z,则a2 015·a2 016=(　　)‎ A.‎3‎ B.‎3‎‎-‎‎1‎‎2‎ ‎ C.2‎3‎-1 D.2〚导学号74920679〛‎ 答案B 解析∵a2 015=‎cos‎2 015π‎6‎,sin‎2 015π‎6‎+cos‎2 015π‎6‎ ‎=cosπ‎6‎,-sinπ‎6‎+cosπ‎6‎‎=‎‎3‎‎2‎‎,‎‎3‎‎-1‎‎2‎,‎ a2 016=‎cos‎2 016π‎6‎,sin‎2 016π‎6‎+cos‎2 016π‎6‎ ‎=(cos 0,sin 0+cos 0)=(1,1),‎ ‎∴a2 015·a2 016=‎3‎‎2‎×1+‎3‎‎-1‎‎2‎×1=‎3‎‎-‎‎1‎‎2‎.故选B.‎ ‎10.已知向量OB=(2,0),向量OC=(2,2),向量CA=(‎2‎cos α,‎2‎sin α),则向量OA与向量OB的夹角的取值范围是(　　)‎ A.‎0,‎π‎4‎ B.π‎4‎‎,‎‎5π‎12‎ ‎ C.‎5π‎12‎‎,‎π‎2‎ D.π‎12‎‎,‎‎5π‎12‎〚导学号74920680〛‎ 答案D 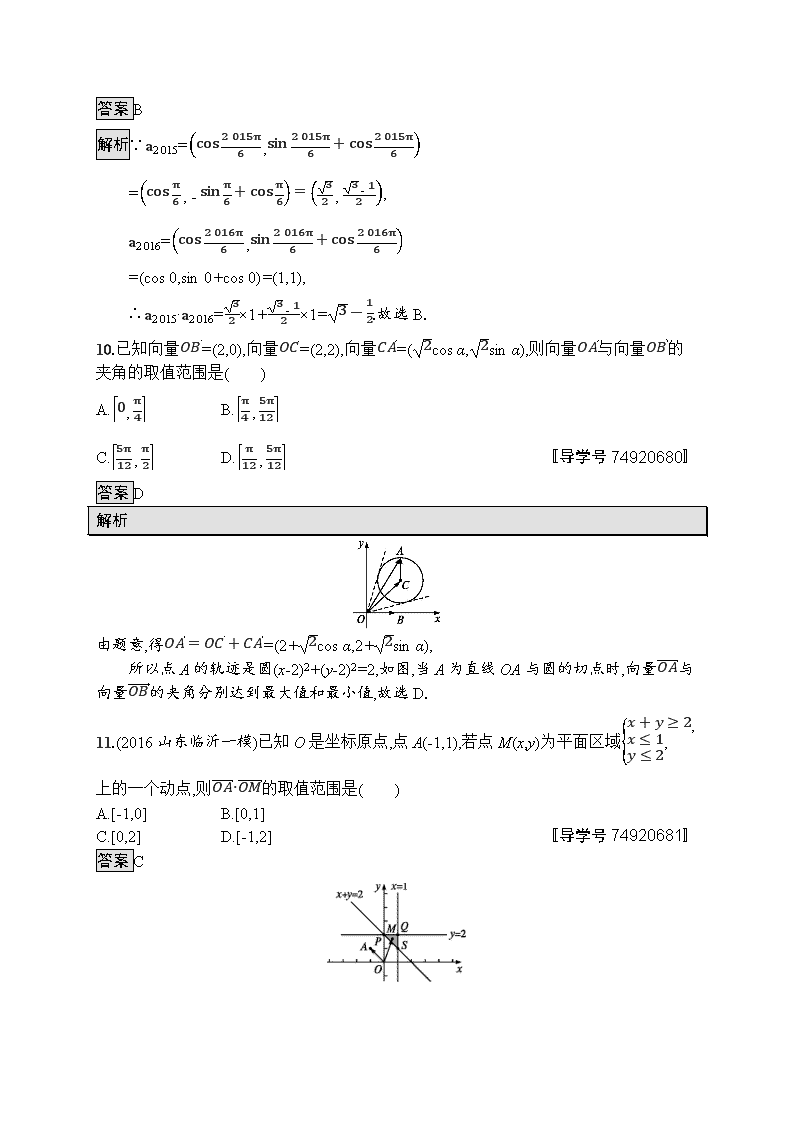解析 由题意,得OA‎=OC+‎CA=(2+‎2‎cos α,2+‎2‎sin α),‎ 所以点A的轨迹是圆(x-2)2+(y-2)2=2,如图,当A为直线OA与圆的切点时,向量OA与向量OB的夹角分别达到最大值和最小值,故选D.‎ ‎11.(2016山东临沂一模)已知O是坐标原点,点A(-1,1),若点M(x,y)为平面区域x+y≥2,‎x≤1,‎y≤2‎上的一个动点,则OA‎·‎OM的取值范围是(　　)‎ A.[-1,0] B.[0,1]‎ C.[0,2] D.[-1,2]〚导学号74920681〛‎ 答案C 解析满足约束条件x+y≥2,‎x≤1,‎y≤2‎的平面区域如图阴影部分所示.‎ 令z=OA‎·‎OM=-x+y,即y=x+z.‎ 当直线y=x+z经过点P(0,2)时,在y轴上的截距最大,从而z最大,即zmax=2.‎ 当直线y=x+z经过点S(1,1)时,在y轴上的截距最小,从而z最小,即zmin=0.‎ 故OA‎·‎OM的取值范围为[0,2],故选C.‎ ‎12.已知|OA|=|OB|=2,点C在线段AB上,且|OC|的最小值为1,则|OA-tOB|(t∈R)的最小值为(　　)‎ A.‎2‎ B.‎3‎ C.2 D.‎5‎〚导学号74920682〛‎ 答案B 解析依题意,可将点A,B置于圆x2+y2=4上;由点C在线段AB上,且|OC|的最小值为1,得原点O到线段AB的距离为1,∠AOB=180°-2×30°=120°,(OA-tOB)2=4+4t2-2t×22cos 120°=4t2+4t+4=4t+‎‎1‎‎2‎‎2‎+3的最小值是3,因此|OA-tOB|的最小值是‎3‎.‎ 二、填空题(本大题共4小题,每小题7分,共28分)‎ ‎13.(2016山东,文13)已知向量a=(1,-1),b=(6,-4).若a⊥(ta+b),则实数t的值为　　　　　. ‎ 答案-5‎ 解析由a⊥(ta+b)可得a·(ta+b)=0,‎ 所以ta2+a·b=0,而a2=12+(-1)2=2,a·b=1×6+(-1)×(-4)=10,所以有t×2+10=0,解得t=-5.‎ ‎14.在矩形ABCD中,AB=2,BC=1,E为BC的中点,若F为该矩形内(含边界)任意一点,则AE‎·‎AF的最大值为　　　　　.〚导学号74920683〛 ‎ 答案‎9‎‎2‎ 解析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立平面直角坐标系,则E‎2,‎‎1‎‎2‎.‎ 设F(x,y),则0≤x≤2,0≤y≤1,‎ 则AE‎·‎AF=2x+‎1‎‎2‎y,令z=2x+‎1‎‎2‎y,当z=2x+‎1‎‎2‎y过点(2,1)时,AE‎·‎AF取最大值‎9‎‎2‎.‎ ‎15.(2016湖北武昌区调考)若向量a,b满足:a=(-‎3‎,1),(a+2b)⊥a,(a+b)⊥b,则|b|=　　　　　. ‎ 答案‎2‎ 解析∵a=(-‎3‎,1),∴|a|=2.‎ ‎∵(a+2b)⊥a,(a+b)⊥b,‎ ‎∴(a+2b)·a=0,(a+b)·b=0,‎ 即|a|2+2a·b=0,①‎ ‎|b|2+a·b=0.②‎ 由①-②×2得|a|2=2|b|2,则|b|=‎2‎.‎ ‎16.在平面直角坐标系中,已知A(1,0),B(0,-1),P是曲线y=‎1-‎x‎2‎上一个动点,则BP‎·‎BA的取值范围是　　　　　　　.〚导学号74920684〛 ‎ 答案[0,‎2‎+1]‎ 解析如图,画出函数y=‎1-‎x‎2‎的图象.‎ 这是以O(0,0)为圆心,以1为半径的一个半圆.‎ 不妨用虚线把这个半圆补充为一个圆.‎ 设BP与BA的夹角为θ,则θ∈[0°,90°].‎ 当θ∈[0°,45°]时,cos (45°-θ)=‎|BP|‎‎2‎,‎ 当θ∈[45°,90°]时,cos (θ-45°)=‎|BP|‎‎2‎.‎ 由于y=cos x,x∈R是偶函数,‎ 所以|BP|=2cos (θ-45°),θ∈[0°,90°].‎ BP‎·‎BA‎=|BP||BA|cos θ=2‎2‎cos (θ-45°)cos θ ‎=2cos2θ+2sin θcos θ=sin 2θ+cos 2θ+1‎ ‎=‎2‎sin (2θ+45°)+1.‎ 因为θ∈[0°,90°],‎ 所以2θ+45°∈[45°,225°].‎ 当2θ+45°=90°,即θ=22.5°时,BP‎·‎BA取最大值‎2‎+1,‎ 当2θ+45°=225°,即θ=90°时,BP‎·‎BA取最小值0,‎ 所以BP‎·‎BA的取值范围是[0,‎2‎+1].‎