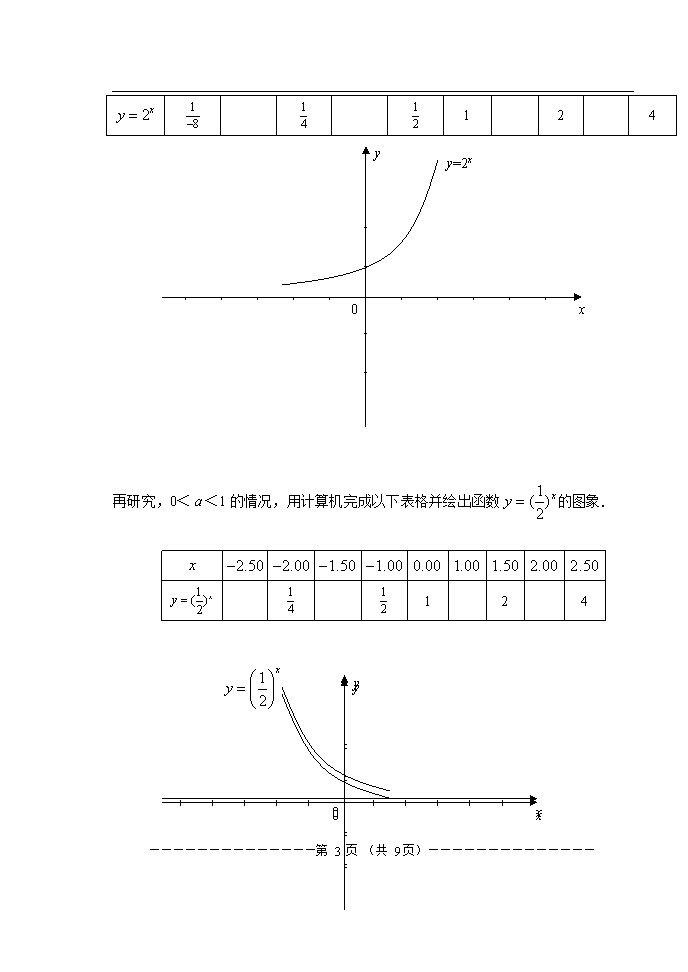指数函数及其性质 9页

‎ ‎ ‎2.1.2指数函数及其性质（2个课时）‎ 一. 教学目标：‎ ‎1．知识与技能 ‎①通过实际问题了解指数函数的实际背景；‎ ‎②理解指数函数的概念和意义，根据图象理解和掌握指数函数的性质.‎ ‎③体会具体到一般数学讨论方式及数形结合的思想；‎ ‎2．情感、态度、价值观 ‎①让学生了解数学来自生活，数学又服务于生活的哲理.‎ ‎②培养学生观察问题，分析问题的能力.‎ ‎3．过程与方法 展示函数图象，让学生通过观察，进而研究指数函数的性质.‎ 二．重、难点 重点：指数函数的概念和性质及其应用.‎ 难点：指数函数性质的归纳，概括及其应用.‎ 三、学法与教具：‎ ‎①学法：观察法、讲授法及讨论法.‎ ‎②教具：多媒体.‎ 第一课时 一．教学设想：‎ ‎1. 情境设置 ‎①在本章的开头，问题（1）中时间与GDP值中的 ‎，请问这两个函数有什么共同特征.‎ ‎ ②这两个函数有什么共同特征 ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ ‎，从而得出这两个关系式中的底数是一个正数，自变量为指数，即都可以用（＞0且≠1来表示）.‎ 二．讲授新课 指数函数的定义 一般地，函数（＞0且≠1）叫做指数函数，其中是自变量，函数的定义域为R.‎ 提问：在下列的关系式中，哪些不是指数函数，为什么？‎ ‎（1） （2） （3）‎ ‎（4） （5） （6）‎ ‎（7） （8） （＞1，且）‎ 小结：根据指数函数的定义来判断说明：因为＞0，是任意一个实数时，是一个确定的实数，所以函数的定义域为实数集R.‎ 若＜0，如在实数范围内的函数值不存在.‎ 若=1, 是一个常量，没有研究的意义，只有满足的形式才能称为指数函数，不符合.‎ 我们在学习函数的单调性的时候，主要是根据函数的图象，即用数形结合的方法来研究. 下面我们通过 先来研究＞1的情况 用计算机完成以下表格，并且用计算机画出函数的图象 ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ ‎1‎ ‎2‎ ‎4‎ y=2x ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ x y ‎0‎ ‎ ‎ ‎ ‎ 再研究，0＜＜1的情况，用计算机完成以下表格并绘出函数的图象.‎ ‎1‎ ‎2‎ ‎4‎ ‎　　　　　　　　　　　　　　　　　　　　　　　‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ x y ‎0‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ ‎-‎ x y ‎0‎ ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ 从图中我们看出 通过图象看出实质是上的 讨论：的图象关于轴对称，所以这两个函数是偶函数，对吗？‎ ‎0‎ ‎②利用电脑软件画出的函数图象. ‎ 问题：1：从画出的图象中，你能发现函数的图象与底数间有什么样的规律.‎ 从图上看（＞1）与（0＜＜1）两函数图象的特征. ‎ ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ ‎0‎ 问题2：根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大（小）值、奇偶性.‎ 问题3：指数函数（＞0且≠1），当底数越大时，函数图象间有什么样的关系.‎ 图象特征 函数性质 ‎＞1‎ ‎0＜＜1‎ ‎＞1‎ ‎0＜＜1‎ 向轴正负方向无限延伸 函数的定义域为R 图象关于原点和轴不对称 非奇非偶函数 函数图象都在轴上方 函数的值域为R+‎ 函数图象都过定点（0，1）‎ ‎=1‎ 自左向右，‎ 图象逐渐上升 自左向右，‎ 图象逐渐下降 增函数 减函数 在第一象限内的图 象纵坐标都大于1‎ 在第一象限内的图 象纵坐标都小于1‎ ‎＞0，＞1‎ ‎＞0，＜1‎ 在第二象限内的图 象纵坐标都小于1‎ 在第二象限内的图 象纵坐标都大于1‎ ‎＜0，＜1‎ ‎＜0，＞1‎ ‎5．利用函数的单调性，结合图象还可以看出：‎ ‎（1）在（＞0且≠1）值域是 ‎（2）若 ‎（3）对于指数函数（＞0且≠1），总有 ‎（4）当＞1时，若＜，则＜；‎ ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ 例题：‎ 例1：（P66 例6）已知指数函数（＞0且≠1）的图象过点（3，π），求 分析：要求再把0，1，3分别代入，即可求得 提问：要求出指数函数，需要几个条件？‎ 课堂练习：P68 练习：第1，2，3题 补充练习：1、函数 ‎ 2、当 解（1）‎ ‎ （2）（－，１）‎ 例2：求下列函数的定义域：‎ ‎（1） （2）‎ 分析：类为的定义域是R，所以，要使（1），（2）题的定义域，保要使其指数部分有意义就得 .‎ ‎3．归纳小结 作业：P69 习题2.1 A组第5、6题 ‎1、理解指数函数 ‎2、解题利用指数函数的图象，可有利于清晰地分析题目，培养数型结合与分类讨论的数学思想 .‎ 第2课时 教学过程：‎ ‎1、复习指数函数的图象和性质 ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ ‎2、例题 例1：（P66例7）比较下列各题中的个值的大小 ‎（1）1.72.5 与 1.73‎ ‎( 2 )与 ‎( 3 ) 1.70.3 与 0.93.1‎ ‎0‎ 解法1：用数形结合的方法，如第（1）小题，用图形计算器或计算机画出的图象，在图象上找出横坐标分别为2.5, 3的点，显然，图象上横坐标就为3的点在横坐标为2.5的点的上方，所以 .‎ 解法2：用计算器直接计算： ‎ 所以，‎ 解法3：由函数的单调性考虑 ‎ 因为指数函数在R上是增函数，且2.5＜3，所以，‎ ‎ 仿照以上方法可以解决第（2）小题 .‎ 注：在第（3）小题中，可以用解法1，解法2解决，但解法3不适合 .‎ ‎ 由于1.70.3=0.93.1不能直接看成某个函数的两个值，因此，在这两个数值间找到1，把这两数值分别与1比较大小，进而比较1.70.3与0.93.1的大小 .‎ 思考：‎ ‎1、已知按大小顺序排列.‎ ‎2. 比较（＞0且≠0）.‎ 指数函数不仅能比较与它有关的值的大小，在现实生活中，也有很多实际的应用.‎ 例2（P67‎ ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ 例8）截止到1999年底，我们人口哟13亿，如果今后，能将人口年平均均增长率控制在1%，那么经过20年后，我国人口数最多为多少（精确到亿）？‎ 分析：可以先考试一年一年增长的情况，再从中发现规律，最后解决问题：‎ ‎1999年底 人口约为13亿 经过1年 人口约为13（1+1%）亿 经过2年 人口约为13（1+1%）（1+1%）=13(1+1%)2亿 经过3年 人口约为13(1+1%)2(1+1%)=13(1+1%)3亿 经过年 人口约为13(1+1%)亿 经过20年 人口约为13(1+1%)20亿 解：设今后人口年平均增长率为1%，经过年后，我国人口数为亿，则 当=20时，‎ 答：经过20年后，我国人口数最多为16亿.‎ 小结：类似上面此题，设原值为N，平均增长率为P，则对于经过时间后总量，＞0且≠1）的函数称为指数型函数 .‎ 思考：P68探究：‎ ‎（1）如果人口年均增长率提高1个平分点，利用计算器分别计算20年后，33年后的我国人口数 .‎ ‎（2）如果年平均增长率保持在2%，利用计算器2020~2100年，每隔5年相应的人口数 .‎ ‎（3）你看到我国人口数的增长呈现什么趋势？‎ ‎（4）如何看待计划生育政策？‎ ‎3．课堂练习 Y=‎ ‎（1）右图是指数函数① ② ③ ④‎ ‎——————————————第 9 页 （共 9页）——————————————‎ ‎ ‎ 的图象，判断与1的大小关系；‎ ‎（2）设其中＞0，≠1，确定为何值时，有：‎ ‎① ②＞ ‎ ‎（3）用清水漂洗衣服，若每次能洗去污垢的，写出存留污垢与漂洗次数的函数关系式，若要使存留的污垢，不超过原有的1%，则少要漂洗几次（此题为人教社B版101页第6题）.‎ 归纳小结：本节课研究了指数函数性质的应用，关键是要记住＞1或0＜＜时的图象，在此基础上研究其性质 .本节课还涉及到指数型函数的应用，形如（a＞0且≠1）.‎ 作业：P69 A组第 7 ，8 题　　　　P70 B组 第 1，4题 ‎——————————————第 9 页 （共 9页）——————————————‎