高考数学专题复习练习第4讲 直线、平面平行的判定及其性质 7页

第4讲 直线、平面平行的判定及其性质 一、选择题 ‎1．若直线m⊂平面α，则条件甲：“直线l∥α”是条件乙：“l∥m”的(　　)．‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 答案　D ‎2．若直线a∥直线b，且a∥平面α，则b与α的位置关系是(　　)‎ A．一定平行 B．不平行 C．平行或相交 D．平行或在平面内 解析 直线在平面内的情况不能遗漏，所以正确选项为D.‎ 答案　D ‎3．一条直线l上有相异三个点A、B、C到平面α的距离相等，那么直线l与平面α的位置关系是 (　　)．‎ A．l∥α B．l⊥α C．l与α相交但不垂直 D．l∥α或l⊂α 解析　l∥α时，直线l上任意点到α的距离都相等；l⊂α时，直线l上所有的点到α的距离都是0；l⊥α时，直线l上有两个点到α距离相等；l与α斜交时，也只能有两个点到α距离相等．‎ 答案　D ‎4．设m，n是平面α内的两条不同直线；l1，l2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是 (　　)．　　　　　　　　　　　　　　　　　　　‎ A．m∥β且l1∥α B．m∥l1且n∥l2‎ C．m∥β且n∥β D．m∥β且n∥l2‎ 解析　对于选项A，不合题意；对于选项B，由于l1与l2是相交直线，而且由l1∥m可得l1∥α，同理可得l2∥α故可得α∥β，充分性成立，而由α∥β不一定能得到l1∥m，它们也可以异面，故必要性不成立，故选B；对于选项C，由于m，n不一定相交，故是必要非充分条件；对于选项D，由n∥l2‎ 可转化为n∥β，同选项C，故不符合题意，综上选B.‎ 答案　B ‎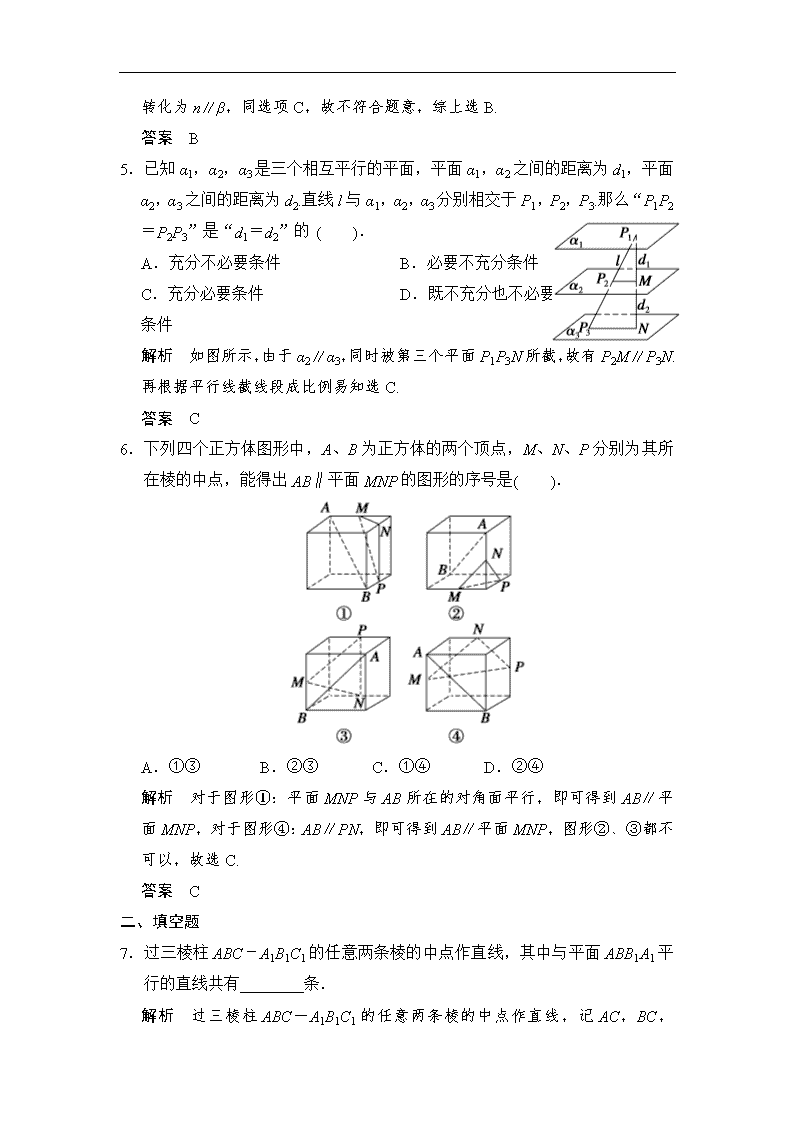5．已知α1，α2，α3是三个相互平行的平面，平面α1，α2之间的距离为d1，平面α2，α3之间的距离为d2.直线l与α1，α2，α3分别相交于P1，P2，P3.那么“P1P2＝P2P‎3”‎是“d1＝d‎2”‎的 (　　)．‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析　如图所示，由于α2∥α3，同时被第三个平面P1P3N所截，故有P‎2M∥P3N.再根据平行线截线段成比例易知选C.‎ 答案　C ‎6．下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是(　　)．‎ A．①③ B．②③ C．①④ D．②④‎ 解析　对于图形①：平面MNP与AB所在的对角面平行，即可得到AB∥平面MNP，对于图形④：AB∥PN，即可得到AB∥平面MNP，图形②、③都不可以，故选C.‎ 答案　C 二、填空题 ‎7．过三棱柱ABC－A1B‎1C1的任意两条棱的中点作直线，其中与平面ABB‎1A1平行的直线共有________条．‎ 解析　过三棱柱ABC－A1B‎1C1的任意两条棱的中点作直线，记AC，BC，‎ A‎1C1，B‎1C1的中点分别为E，F，E1，F1，则直线EF，E‎1F1，EE1，FF1，E‎1F，EF1均与平面ABB‎1A1平行，故符合题意的直线共6条．‎ 答案　6‎ ‎8．α、β、γ是三个平面，a、b是两条直线，有下列三个条件：①a∥γ，b⊂β；②a∥γ，b∥β；③b∥β，a⊂γ.如果命题“α∩β＝a，b⊂γ，且________，则a∥b”为真命题，则可以在横线处填入的条件是________(把所有正确的题号填上)．‎ 解析　①中，a∥γ，a⊂β，b⊂β，β∩γ＝b⇒a∥b(线面平行的性质)．③中，b∥β，b⊂γ，a⊂γ，β∩γ＝a⇒a∥b(线面平行的性质)．‎ 答案　①③‎ ‎9．若m、n为两条不重合的直线，α、β为两个不重合的平面，则下列命题中真命题的序号是________．‎ ‎①若m、n都平行于平面α，则m、n一定不是相交直线；‎ ‎②若m、n都垂直于平面α，则m、n一定是平行直线；‎ ‎③已知α、β互相平行，m、n互相平行，若m∥α，则n∥β；‎ ‎④若m、n在平面α内的射影互相平行，则m、n互相平行．‎ 解析　①为假命题，②为真命题，在③中，n可以平行于β，也可以在β内，故是假命题，在④中，m、n也可能异面，故为假命题．‎ 答案　②‎ ‎10．对于平面α与平面β，有下列条件：①α、β都垂直于平面γ；②α、β都平行于平面γ；③α内不共线的三点到β的距离相等；④l，m为两条平行直线，且l∥α，m∥β；⑤l，m是异面直线，且l∥α，m∥α；l∥β，m∥β，则可判定平面α与平面β平行的条件是________(填正确结论的序号)．‎ 解析　由面面平行的判定定理及性质定理知，只有②⑤能判定α∥β.‎ 答案　②⑤‎ 三、解答题 ‎11． 如图，在四面体A－BCD中，F、E、H分别是棱AB、BD、AC的中点，G为DE的中点．证明：直线HG∥平面CEF.‎ 证明　法一　如图，连接BH，BH与CF交于K，连接EK.‎ ‎∵F、H分别是AB、AC的中点，‎ ‎∴K是△ABC的重心，‎ ‎∴＝.‎ 又据题设条件知，＝，‎ ‎∴＝，∴EK∥GH.‎ ‎∵EK⊂平面CEF，GH⊄平面CEF，‎ ‎∴直线HG∥平面CEF.‎ 法二　如图，取CD的中点N，连接GN、HN.‎ ‎∵G为DE的中点，∴GN∥CE.‎ ‎∵CE⊂平面CEF，GN⊄平面CEF，∴GN∥平面CEF.‎ 连接FH，EN ‎∵F、E、H分别是棱AB、BD、AC的中点，‎ ‎∴FH綉BC，EN綉BC，∴FH綉EN，‎ ‎∴四边形FHNE为平行四边形，∴HN∥EF.‎ ‎∵EF⊂平面CEF，HN⊄平面CEF，‎ ‎∴HN∥平面CEF.HN∩GN＝N，‎ ‎∴平面GHN∥平面CEF.‎ ‎∵GH⊂平面GHN，∴直线HG∥平面CEF.‎ ‎12． 如图，已知ABCD－A1B‎1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE＝FC1＝B‎1G＝1，H是B‎1C1的中点．‎ ‎(1)求证：E，B，F，D1四点共面；‎ ‎(2)求证：平面A1GH∥平面BED‎1F.‎ 证明　(1)∵AE＝B‎1G＝1，∴BG＝A1E＝2，‎ ‎∴BG綉A1E，∴A‎1G綉BE.‎ 又同理，C‎1F綉B‎1G，∴四边形C1FGB1是平行四边形，‎ ‎∴FG綉C1B1綉D‎1A1，∴四边形A1GFD1是平行四边形．‎ ‎∴A‎1G綉D‎1F，∴D‎1F綉EB，‎ 故E、B、F、D1四点共面．‎ ‎(2)∵H是B‎1C1的中点，∴B1H＝.‎ 又B‎1G＝1，∴＝.‎ 又＝，且∠FCB＝∠GB1H＝90°，‎ ‎∴△B1HG∽△CBF，∴∠B1GH＝∠CFB＝∠FBG，‎ ‎∴HG∥FB.‎ 又由(1)知A‎1G∥BE，且HG∩A‎1G＝G，‎ FB∩BE＝B，∴平面A1GH∥平面BED‎1F.‎ ‎13．一个多面体的直观图及三视图如图所示：(其中M、N分别是AF、BC的中点)．‎ ‎(1)求证：MN∥平面CDEF；‎ ‎(2)求多面体A－CDEF的体积．‎ 解　由三视图可知：AB＝BC＝BF＝2，DE＝CF＝2，∠CBF＝.‎ ‎(1)证明：取BF的中点G，连接MG、NG，由M、N分别为AF、BC的中点可得，NG∥CF，MG∥EF，‎ ‎∴平面MNG∥平面CDEF，‎ 又MN⊂平面MNG，‎ ‎∴MN∥平面CDEF.‎ ‎(2)取DE的中点H.‎ ‎∵AD＝AE，∴AH⊥DE，‎ 在直三棱柱ADE－BCF中，平面ADE⊥平面CDEF，‎ 平面ADE∩平面CDEF＝DE.‎ ‎∴AH⊥平面CDEF.‎ ‎∴多面体A－CDEF是以AH为高，以矩形CDEF为底面的棱锥，在△ADE中，AH＝.S矩形CDEF＝DE·EF＝4，‎ ‎∴棱锥A－CDEF的体积为V＝·S矩形CDEF·AH＝×4×＝.‎ ‎14．如图所示，四边形ABCD为矩形，AD⊥平面ABE，AE＝EB＝BC，F为CE上的点，且BF⊥平面ACE.‎ ‎(1)求证：AE⊥BE；‎ ‎(2)设M在线段AB上，且满足AM＝2MB，试在线段CE上确定一点N，使得MN∥平面DAE.‎ ‎(1)证明　∵AD⊥平面ABE，AD∥BC，‎ ‎∴BC⊥平面ABE，‎ 又AE⊂平面ABE，则AE⊥BC.‎ 又∵BF⊥平面ACE，AE⊂平面ABE，‎ ‎∴AE⊥BF，‎ 又BC∩BF＝B，∴AE⊥平面BCE，‎ 又BE⊂平面BCE，∴AE⊥BE.‎ ‎(2)解　在△ABE中过M点作MG∥AE交BE于G点，在△BEC中过G点作GN∥BC交EC于N点，连接MN，则由比例关系易得CN＝CE.‎ ‎∵MG∥AE，MG⊄平面ADE，AE⊂平面ADE，‎ ‎∴MG∥平面ADE.‎ 同理，GN∥平面ADE.‎ 又∵GN∩MG＝G，∴平面MGN∥平面ADE.‎ 又MN⊂平面MGN，‎ ‎∴MN∥平面ADE.‎ ‎∴N点为线段CE上靠近C点的一个三等分点.‎