高中数学第一章集合与函数概念1_2函数及其表示第2课时课堂探究学案新人教A版必修11 4页

1.2 函数及其表示 课堂探究 探究一列表法表示函数 列表法是表示函数的重要方法，这如同我们在画函数图象时所列的表，它的明显优点是 变量对应的函数值在表中可直接找到，不需计算． 【典型例题 1】 已知函数 f(x)，g(x)分别由下表给出： x 1 2 3 f(x) 2 1 1 x 1 2 3 g(x) 3 2 1 则 f(g(1))的值为______；当 g(f(x))＝2 时，x＝______. 思路分析：这是用列表法表示的函数求值问题，在解答时，找准变量对应的值即可． 解析：由 g(x)对应表，知 g(1)＝3，∴f(g(1))＝f(3)． 由 f(x)对应表，得 f(3)＝1， ∴f(g(1))＝f(3)＝1. 由 g(x)对应表，得当 x＝2 时，g(2)＝2. 又 g(f(x))＝2， ∴f(x)＝2. 又由 f(x)对应表，得 x＝1 时，f(1)＝2. ∴x＝1. 答案：1 1 探究二 求函数的解析式 求函数解析式实际上就是寻找函数三要素中的对应关系，也就是在已知自变量和函数值 的条件下求对应关系．解答此类问题时，可根据已知条件选择不同的方法求解． 求函数解析式的常用方法： (1)待定系数法：若已知函数的类型，可用待定系数法求解，即由函数类型设出函数解 析式，再根据条件列方程(或方程组)，通过解方程(组)求出待定系数，进而求出函数解析式． (2)换元法(有时可用“配凑法”)：已知函数 f(g(x))的解析式求 f(x)的解析式可用换 元法(或“配凑法”)，即令 g(x)＝t，反解出 x，然后代入 f(g(x))中求出 f(t)，从而求出 f(x)． 【典型例题 2】 (1)已知 f(x＋1)＝x2－3x＋2，求 f(x)； (2)已知 f 1x x     ＝x2＋ 2 1 x ，求 f(x)； (3)已知 f(x)是二次函数，且满足 f(0)＝1，f(x＋1)－f(x)＝2x，求 f(x)的解析式． 思路分析：(1)令 x＋1＝t，代入 f(x＋1)＝x2－3x＋2 可得 f(x)；(2)将 x2＋ 2 1 x 变形， 使其变为关于 x＋ 1 x 的形式，可得 f(x)；(3)设出 f(x)＝ax2＋bx＋c(a≠0)，再根据条件列 出方程组求出 a，b，c 的值． 解：(1)令 x＋1＝t，则 x＝t－1，将 x＝t－1 代入 f(x＋1)＝x2－3x＋2，得 f(t)＝(t －1)2－3(t－1)＋2＝t2－5t＋6， ∴f(x)＝x2－5x＋6. (2)f 1x x     ＝x2＋ 2 1 x ＝ 1x x     2－2， ∴f(x)＝x2－2. (3)设所求的二次函数为 f(x)＝ax2＋bx＋c(a≠0)． ∵f(0)＝1，∴c＝1，则 f(x)＝ax2＋bx＋1. 又∵f(x＋1)－f(x)＝2x，对任意 x∈R 成立， ∴a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x， 即 2ax＋a＋b＝2x， 由恒等式性质，得 2 2 0 a a b    ＝ ， ＋ ＝ ，∴ 1 1. a b    ＝ ， ＝－ ∴所求二次函数为 f(x)＝x2－x＋1. 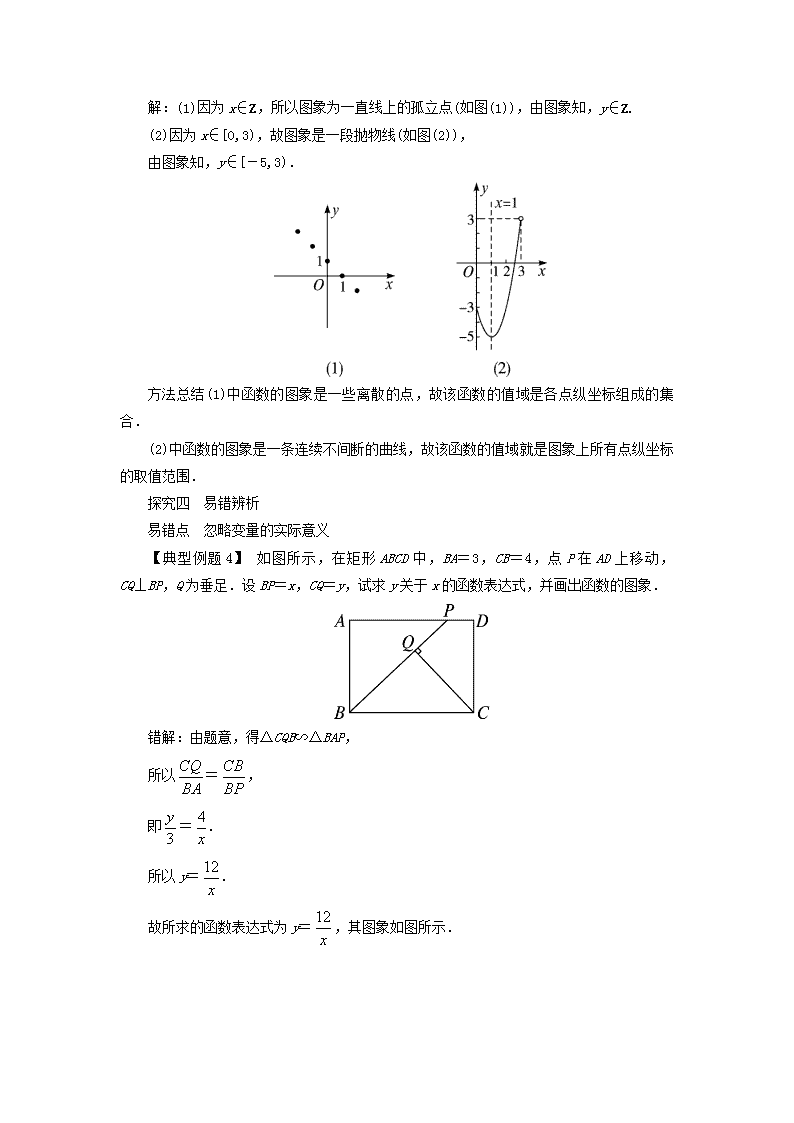探究三 函数的图象 函数的图象能直观地反映出函数的一些性质，因此，解答函数问题时常常借助于图象． 1．作函数图象主要有三步：列表、描点、连线．作图象时一般应先确定函数的定义域， 再在定义域内化简函数解析式，最后列表画出图象． 2．函数的图象可能是平滑的曲线，也可能是一群孤立的点，画图时要注意关键点，如 图象与坐标轴的交点、区间端点，二次函数的顶点等等，还要分清这些关键点是实心点还是 空心圆圈． 【典型例题 3】 作出下列函数图象并求其值域． (1)y＝1－x(x∈Z)； (2)y＝2x2－4x－3(0≤x<3)． 解：(1)因为 x∈Z，所以图象为一直线上的孤立点(如图(1))，由图象知，y∈Z. (2)因为 x∈[0,3)，故图象是一段抛物线(如图(2))， 由图象知，y∈[－5,3)． 方法总结(1)中函数的图象是一些离散的点，故该函数的值域是各点纵坐标组成的集合． (2)中函数的图象是一条连续不间断的曲线，故该函数的值域就是图象上所有点纵坐标 的取值范围． 探究四 易错辨析 易错点 忽略变量的实际意义 【典型例题 4】 如图所示，在矩形 ABCD 中，BA＝3，CB＝4，点 P 在 AD 上移动，CQ⊥BP， Q 为垂足．设 BP＝x，CQ＝y，试求 y 关于 x 的函数表达式，并画出函数的图象． 错解：由题意，得△CQB∽△BAP， 所以 CQ BA ＝ CB BP ， 即 3 y ＝ 4 x . 所以 y＝12 x . 故所求的函数表达式为 y＝12 x ，其图象如图所示． 错因分析：没有考虑 x 的实际意义，扩大了 x 的取值范围，导致出错． 正解：由题意，得△CQB∽△BAP， 所以 CQ BA ＝ CB BP ，即 3 y ＝ 4 x .所以 y＝12 x . 因为 BA≤BP≤BD，而 BA＝3，CB＝AD＝4， 所以 BD＝ 2 23 4 ＝5， 所以 3≤x≤5， 故所求的函数表达式为 y＝12 x (3≤x≤5)． 如图所示，曲线 MN 就是所求的函数图象． 反思从实际问题中得到的函数，求其定义域时，不仅要使函数有意义，而且还要使实际 问题有意义．