高中数学第一章集合第3节集合的基本运算第1课时基础知识素材北师大版必修11 4页

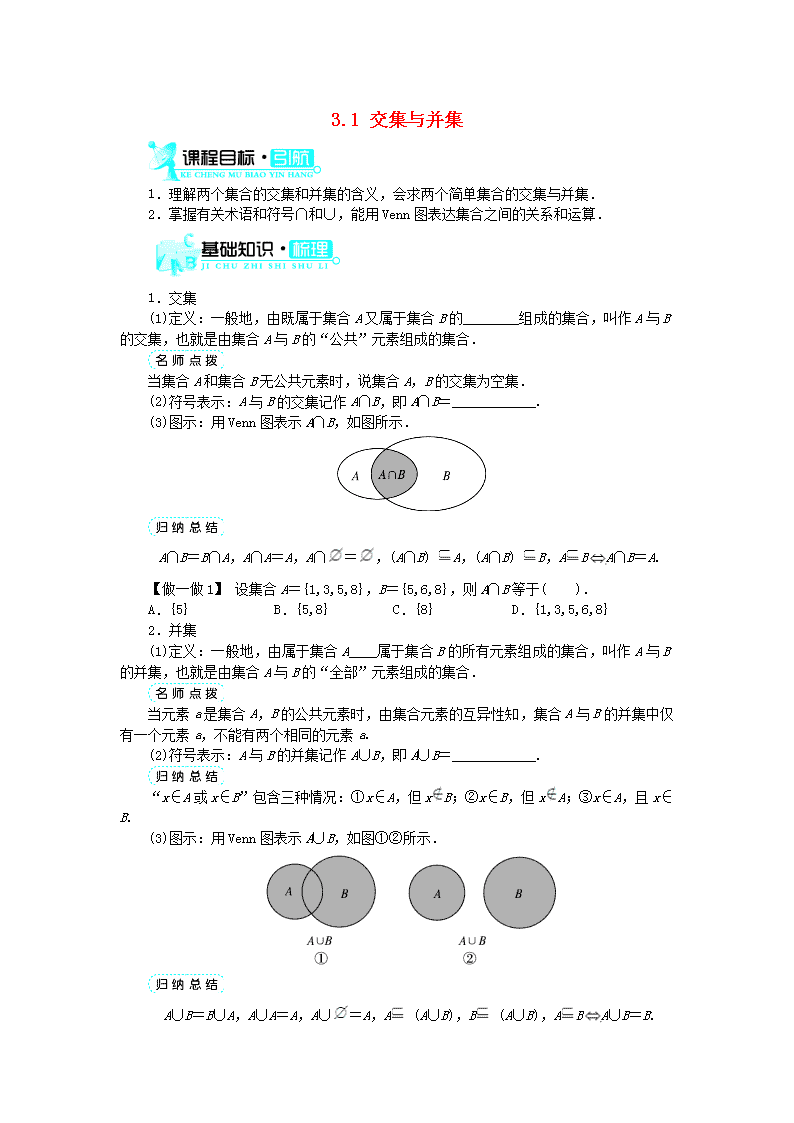
3.1 交集与并集 1．理解两个集合的交集和并集的含义，会求两个简单集合的交集与并集． 2．掌握有关术语和符号∩和∪，能用 Venn 图表达集合之间的关系和运算． 1．交集 (1)定义：一般地，由既属于集合 A 又属于集合 B 的________组成的集合，叫作 A 与 B 的交集，也就是由集合 A 与 B 的“公共”元素组成的集合． 当集合 A 和集合 B 无公共元素时，说集合 A，B 的交集为空集． (2)符号表示：A 与 B 的交集记作 A∩B，即 A∩B＝____________. (3)图示：用 Venn 图表示 A∩B，如图所示． A∩B＝B∩A，A∩A＝A，A∩ ＝ ，(A∩B) A，(A∩B) B，A B A∩B＝A. 【做一做 1】 设集合 A＝{1,3,5,8}，B＝{5,6,8}，则 A∩B 等于( )． A．{5} B．{5,8} C．{8} D．{1,3,5,6,8} 2．并集 (1)定义：一般地，由属于集合 A____属于集合 B 的所有元素组成的集合，叫作 A 与 B 的并集，也就是由集合 A 与 B 的“全部”元素组成的集合． 当元素 a 是集合 A，B 的公共元素时，由集合元素的互异性知，集合 A 与 B 的并集中仅 有一个元素 a，不能有两个相同的元素 a. (2)符号表示：A 与 B 的并集记作 A∪B，即 A∪B＝____________. “x∈A 或 x∈B”包含三种情况：①x∈A，但 x B；②x∈B，但 x A；③x∈A，且 x∈ B. (3)图示：用 Venn 图表示 A∪B，如图①②所示． A∪B＝B∪A，A∪A＝A，A∪ ＝A，A (A∪B)，B (A∪B)，A B A∪B＝B. 【做一做 2】 已知集合 A＝{x|x＞0}，B＝{x|－1≤x≤2}，则 A∪B 等于( )． A．{x|x≥－1} B．{x|x≤2} C．{x|0＜x≤2} D．{x|－1≤x≤2} 答案：1．(1)所有元素 (2){x|x∈A，且 x∈B} 【做一做 1】 B 依据交集的定义，用 Venn 图表示或观察 A，B 中的元素，如图所示， 可得 A∩B＝{5,8}． 2．(1)或 (2){x|x∈A，或 x∈B} 【做一做 2】 A 用数轴表示集合 A 和 B，如图所示， 则阴影部分就是 A∪B， 所以 A∪B＝{x|x≥－1}． 1．对于 A∩B＝ ，存在哪几种可能的情况？ 剖析：存在三种情况： (1)集合 A，B 均为空集； (2)集合 A，B 中有一个是空集； (3)集合 A，B 均为非空集，但无相同元素． 2．为什么集合{x|x∈A，或 x∈B}与集合{x|x∈A，且 x∈B}不一定相等？ 剖析：在数学中，“或”表示至少有一个成立，而“且”表示都成立．“x∈A，或 x∈ B”表示元素 x 可能在集合 A 中，也可能在集合 B 中，也可能同时在集合 A 和 B 中，因此集 合{x|x∈A，或 x∈B}是集合 A 和 B 的并集．而“x∈A，且 x∈B”仅表示元素 x 同时在集合 A 和 B 中，即是集合 A 和 B 的公共元素，因此集合{x|x∈A，且 x∈B}表示集合 A 和 B 的交集．所 以这两个集合不一定相等，并且有{x|x∈A，且 x∈B} {x|x∈A，或 x∈B}． 例如，集合 A＝{1,2,3}，集合 B＝{3,4}，则集合{x|x∈A，或 x∈B}＝{1,2,3,4}＝A∪ B，而集合{x|x∈A，且 x∈B}＝{3}＝A∩B.很明显此时{x|x∈A，或 x∈B}≠{x|x∈A，且 x ∈B}，且{x|x∈A，且 x∈B} {x|x∈A，或 x∈B}． 题型一 集合的基本运算 【例 1】 已知集合 A＝{x|－4≤x＜2}，B＝{x|－1＜x≤3}，求 A∩B，A∪B. 分析：已知集合 A，B 都是无限集合，要求 A∩B，A∪B，可借助数轴直观求解． 反思：利用数形结合的思想，将满足条件的集合在数轴上一一表示出来，从而求出集合 的交集、并集，是必须掌握且要熟练运用的方法． 题型二 交集与并集的综合应用 【例 2】设集合 A＝{|a＋1|,3,5}，集合 B＝{2a＋1，a2＋2a，a2＋2a－1}，当 A∩B＝{2,3} 时，求 A∪B. 分析：欲求 A∪B，关键在于求出 a，由条件 A∩B＝{2,3}，根据交集的定义，可得|a＋ 1|＝2，从而求出 A，B. 反思：本例中，抓住 A∩B＝{2,3}，联想交集性质 A∩B A，从而得到 2 和 3 均在 A 中， 推知|a＋1|＝2.由此可知捕捉解题的“题眼”，找到解题切入点，是顺利解题的关键，若已 知中含有未知字母(或参数)，在解出未知字母(或参数)后，应代入原集合进行检验，最后再 进行并、交运算． 题型三 由集合间的关系求参数的取值范围 【例 3】 设集合 A＝{x|x2－x－2＝0}，B＝{x|x2＋x＋a＝0}，若 A∪B＝A，求实数 a 的 取值范围． 分析：集合 A，B 均是关于 x 的一元二次方程的解集，由 A∪B＝A 可得 B A，通过讨论 集合 B 是否为空集来求得 a 的取值范围． 反思：通过深刻理解集合表示法的转换及集合之间的关系，把求参数取值范围问题转化 为不等式、方程等常见的数学问题，这称为数学的转化与化归思想，也是常用的数学方法． 解本题时，特别容易出现的错误是遗漏了 B＝ 的情形，其原因是对 B A 的理解不够 充分．对于 B A，当 A≠ 时，则有 B＝ 或 B≠ .避免出错的方法是培养分类讨论的数 学思想方法和注意经验的积累． 答案：【例 1】 解：分别在数轴上表示集合 A 和 B， 根据 A∩B，A∪B 的定义，由图知，A∩B＝{x|－1＜x＜2}，A∪B＝{x|－4≤x≤3}． 【例 2】 解：∵2∈A，∴|a＋1|＝2.∴a＝1 或 a＝－3. 当 a＝1 时，集合 B 的元素 a2＋2a＝3,2a＋1＝3.由集合元素的互异性知 a≠1. 当 a＝－3 时，2a＋1＝－5，a2＋2a＝3，a2＋2a－1＝2，即集合 B＝{－5,3,2}．∴A∪B ＝{－5,2,3,5}． 【例 3】 解：A＝{x|x2－x－2＝0}＝{－1,2}，B 是关于 x 的方程 x2＋x＋a＝0 的解集． ∵A∪B＝A，∴B A. ∵A＝{－1,2}≠ ，∴B＝ 或 B≠ . 当 B＝ 时，即关于 x 的方程 x2＋x＋a＝0 无实数解，则有Δ＝1－4a＜0，即此时有 a ＞1 4 . 当 B≠ 时，即关于 x 的方程 x2＋x＋a＝0 有实数解． 若 B 中仅有一个元素，则Δ＝0，即 a＝1 4 ， 此时 B＝ x|x2＋x＋1 4 ＝0 ＝ －1 2 . ∵－1 2 A，∴B 不是 A 的子集，即 a＝1 4 不合题意． 若 B 中含有两个元素，则必有 B＝{－1,2}，则－1 和 2 是关于 x 的方程 x2＋x＋a＝0 的 解， ∴ －1＋2＝－1， －1× 2＝a， 即 1＝－1， a＝－2. ∵1≠－1，∴此时不合题意． 综上可得，实数 a 的取值范围是 a|a>1 4 . 1 (2010 广东高考，文 1)若集合 A＝{0,1,2,3}，B＝{1,2,4}，则集合 A∪B＝( )． A．{0,1,2,3,4} B．{1,2,3,4} C．{1,2} D．{0} 2 若集合 P＝{x|x2＝1}，M＝{x|x2－2x－3＝0}，则 P∩M 等于( )． A．{3} B．{1} C．{－1} D． 3 已知集合 A＝{x|x＜a}，B＝{x|x≤1，或 x≥2}，且 A∪B＝R，则实数 a 的取值范围 是( )． A．a≤1 B．a＜1 C．a≥2 D．a＞2 4 若集合 A＝{x|x≤2}，B＝{x|x≥a}满足 A∩B＝{2}，则实数 a＝__________. 5 (2010 福州三中期中，17)已知集合 A＝{2，a－1}，B＝{a2－7，－1}，且 A∩B＝{2}， 求实数 a 的值． 答案：1．A 因为 A＝{0,1,2,3}，B＝{1,2,4}， 所以 A∪B＝{0,1,2,3,4}． 2．C P＝{x|x2＝1}＝{－1,1}，M＝{x|x2－2x－3＝0}＝{－1,3}．所以 P∩M＝{－1}， 故选 C. 3．C 如图所示，要使 A∪B＝R，则 a 位于 2 的右边或与 2 重合，即 a≥2. 4．2 ∵A∩B＝{x|a≤x≤2}＝{2}，∴a＝2. 5．解：∵A∩B＝{2}，∴2∈A 且 2∈B. ∴a2－7＝2.∴a＝3 或 a＝－3. 当 a＝3 时，集合 A 中的元素 a－1＝2，不符合集合中元素的互异性，∴a＝3 舍去． 当 a＝－3 时，A＝{2，－4}，B＝{2，－1}，符合已知 A∩B＝{2}． 综上所述，a＝－3.