高中数学第二章基本初等函数Ⅰ2_2对数函数第3课时课堂探究学案新人教A版必修11 3页

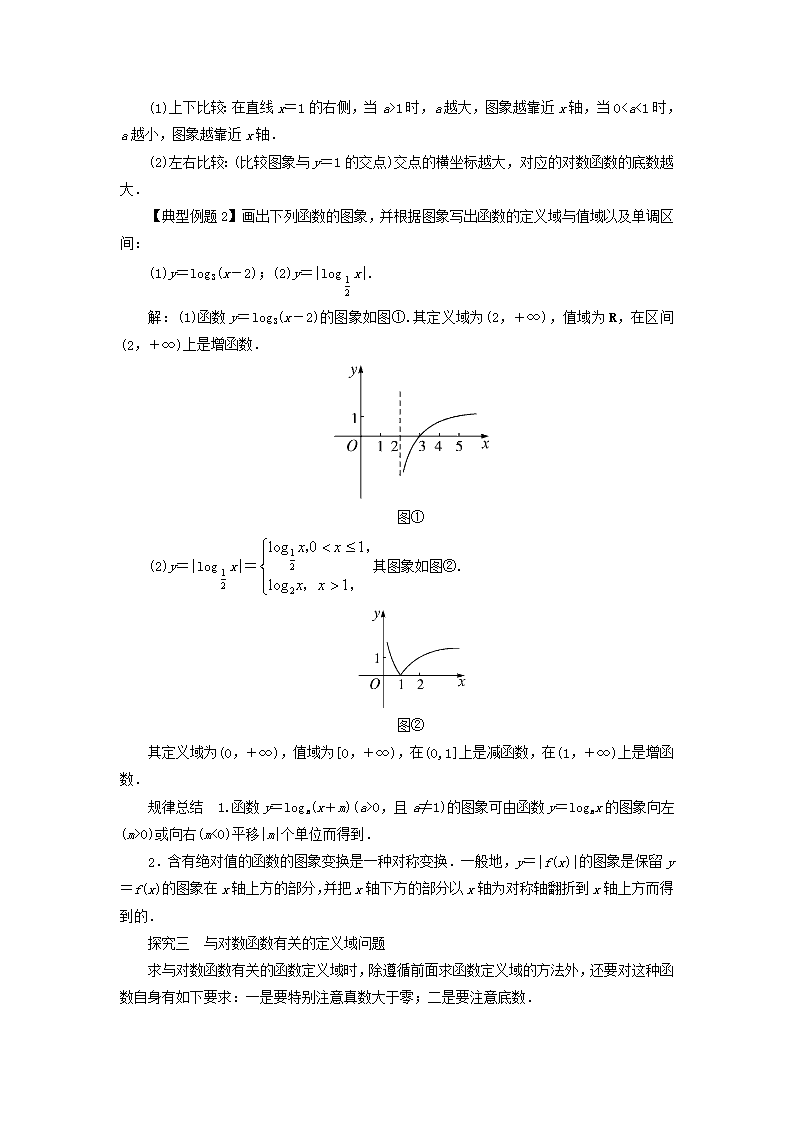
2.2 对数函数 课堂探究 探究一 对数函数的概念 判断一个函数是对数函数必须是形如 y＝logax(a>0，且 a≠1)的形式，即必须满足以下 条件： (1)系数为 1. (2)底数为大于 0 且不等于 1 的常数． (3)对数的真数仅有自变量 x. 【典型例题 1】 下列函数中，哪些是对数函数？ (1)y＝logax2(a>0，且 a≠1)； (2)y＝log2x－1； (3)y＝2log8x； (4)y＝logxa(x>0，且 x≠1)； (5)y＝log5x. 思路分析：根据对数函数的定义进行判断． 解：只有(5)为对数函数． (1)中真数不是自变量 x，故不是对数函数； (2)中对数式后减 1，故不是对数函数； (3)中 log8x 前的系数是 2，而不是 1， 故不是对数函数； (4)中底数是自变量 x，而非常数 a，故不是对数函数． 探究二 对数函数的图象问题 1．画对数函数 y＝logax 的图象时，应牢牢抓住三个关键点(a,1)，(1,0)， 1 , 1a     . 2．对数函数图象与直线 y＝1 的交点横坐标越大，则对应的对数函数的底数越大． 3．函数 y＝logax(a>0，且 a≠1)的底数变化对图象位置的影响 观察图象，注意变化规律： (1)上下比较：在直线 x＝1 的右侧，当 a>1 时，a 越大，图象越靠近 x 轴，当 00，且 a≠1)的图象可由函数 y＝logax 的图象向左 (m>0)或向右(m<0)平移|m|个单位而得到． 2．含有绝对值的函数的图象变换是一种对称变换．一般地，y＝|f(x)|的图象是保留 y ＝f(x)的图象在 x 轴上方的部分，并把 x 轴下方的部分以 x 轴为对称轴翻折到 x 轴上方而得 到的． 探究三 与对数函数有关的定义域问题 求与对数函数有关的函数定义域时，除遵循前面求函数定义域的方法外，还要对这种函 数自身有如下要求：一是要特别注意真数大于零；二是要注意底数． 【典型例题 3】 求下列函数的定义域： (1)y＝ lg 2 x   ； (2)y＝ 3 1 log 3 2x   ； (3)y＝ 4log 4 3 x x     . 解：(1)要使函数式有意义，则 lg(2－x)≥0， ∴ 2 0 2 1 x x    － ， － ，∴x≤1. 故函数的定义域为(－∞，1]． (2)要使函数式有意义，则 log3(3x－2)≠0， ∴ 3 2 0 3 2 1 x x    － ， － ， ∴x> 2 3 ，且 x≠1. 故函数的定义域为 2 ,13      ∪(1，＋∞)． (3)要使函数有意义，则有 4 0 3 0 x x    － ， － ，解得 x<4，且 x≠3， 故函数的定义域为(－∞，3)∪(3,4)． 探究四 易错辨析 易错点 求函数的定义域时先对解析式变形 【典型例题 4】 已知函数 f(x)＝log5(x－1)2，求 f(x)的定义域． 错解：f(x)＝2log5(x－1)，要使 f(x)有意义，则 x－1>0，解得 x>1，则 f(x)的定义域 是(1，＋∞)． 错因分析：错解中，由于对 f(x)的解析式变形后再求定义域，导致出错． 正解：要使 f(x)有意义，则(x－1)2>0，解得 x≠1，则 f(x)的定义域是(－∞，1)∪(1， ＋∞)． 反思求函数 f(x)的定义域时，不能对 f(x)的解析式变形，否则会导致求出的定义域“变 大”或“缩小”．