2020-2021学年数学新教材人教B版必修第四册教案：第9章 章末综合提升 11页

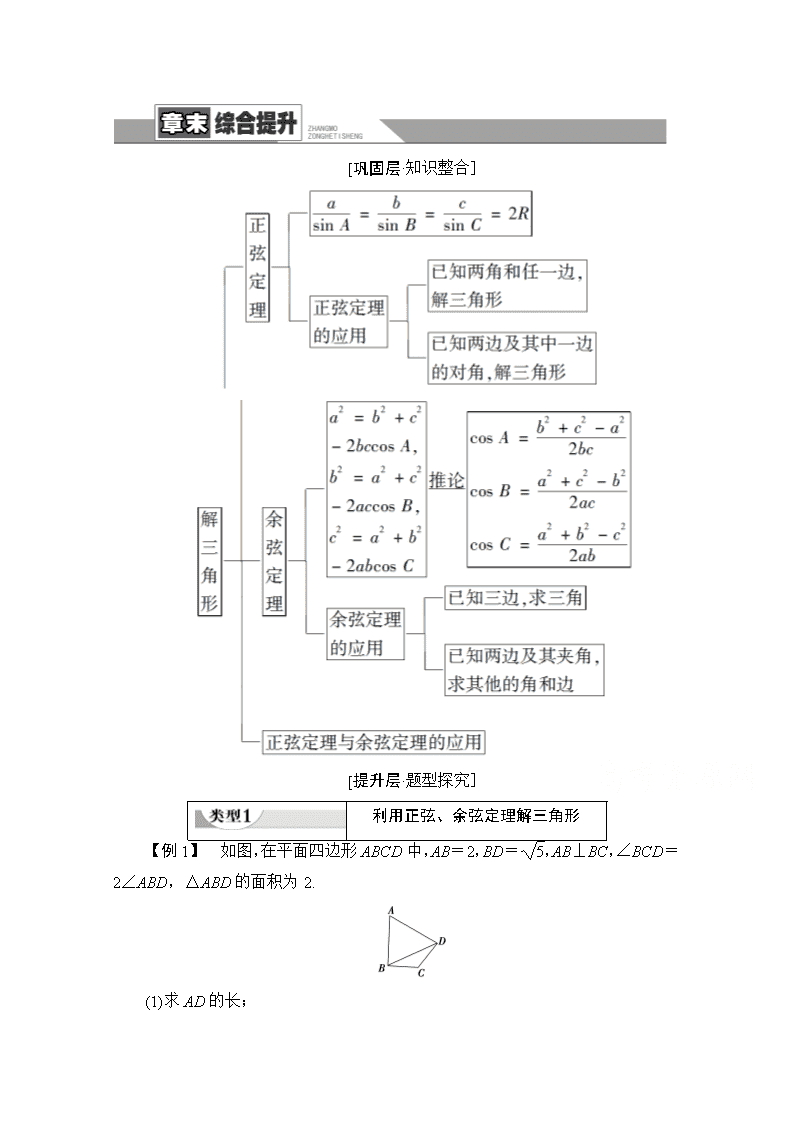
www.ks5u.com ‎[巩固层·知识整合]‎ ‎[提升层·题型探究]‎ 利用正弦、余弦定理解三角形 ‎【例1】　如图，在平面四边形ABCD中，AB＝2，BD＝，AB⊥BC，∠BCD＝2∠ABD，△ABD的面积为2.‎ ‎(1)求AD的长；‎ ‎(2)求△CBD的面积．‎ ‎[思路探究]　(1)由面积公式求出sin∠ABD，进而得cos∠ABD的值，利用余弦定理可解；‎ ‎(2)由AB⊥BC可以求出sin∠CBD的大小，再由二倍角公式求出sin∠BCD，可判断△CBD为等腰三角形，利用正弦定理求出CD的大小，最后利用面积公式求解．‎ ‎[解]　(1)由S△ABD＝AB·BD·sin∠ABD＝×2××sin∠ABD＝2，可得sin∠ABD＝，‎ 又∠ABD∈，所以cos∠ABD＝.‎ 在△ABD中，由AD2＝AB2＋BD2－2·AB·BD·cos∠ABD，‎ 可得AD2＝5，所以AD＝.‎ ‎(2)由AB⊥BC，得∠ABD＋∠CBD＝，‎ 所以sin∠CBD＝cos∠ABD＝.‎ 又∠BCD＝2∠ABD，所以sin∠BCD＝2sin∠ABD·cos∠ABD＝，∠BDC＝π－∠CBD－∠BCD＝π－－2∠ABD＝－∠ABD＝∠CBD，‎ 所以△CBD为等腰三角形，即CB＝CD.‎ 在△CBD中，由正弦定理知，＝，‎ 得CD＝＝＝，‎ 所以S△CBD＝×××＝.‎ 利用正、余弦定理解三角形要注意以下几个方面 ‎(1)画图，把相关数据标注在三角形中，便于确定已知和所求．‎ ‎(2)明确解题过程中所使用的定理，有些题目两个定理都适用．‎ ‎(3)注意对三角形内角和定理、大边对大角的应用，避免出现增解或漏解的错误．‎ ‎(4)多边形中的边角计算问题通常化归到三角形中利用正、余弦定理求解．‎ ‎1．如图所示，在△ABC中，B＝，AB＝8，点D在BC边上，CD＝2，cos∠ADC＝.‎ ‎(1)求sin∠BAD；‎ ‎(2)求BD，AC的长．‎ ‎[解]　(1)在△ADC中，‎ 因为cos∠ADC＝，‎ 所以sin∠ADC＝，‎ 所以sin∠BAD＝sin(∠ADC－B)‎ ‎＝sin∠ADCcos B－cos∠ADCsin B ‎＝×－×＝.‎ ‎(2)在△ABD中，由正弦定理，得BD＝＝＝3.‎ 在△ABC中，由余弦定理，‎ 得AC2＝AB2＋BC2－2AB×BC×cos B ‎＝82＋52－2×8×5×＝49，‎ 所以AC＝7.‎ 三角变换与解三角形的综合问题 角度1　三角形形状的判断 ‎【例2】　在△ABC中，若(a2＋b2)sin(A－B)＝(a2－b2)·sin(A＋B)，试判断△ABC的形状．‎ ‎[解]　∵(a2＋b2)sin(A－B)＝(a2－b2)sin(A＋B)，‎ ‎∴b2[sin(A＋B)＋sin(A－B)]‎ ‎＝a2[sin(A＋B)－sin(A－B)]，‎ ‎∴2b2sin Acos B＝‎2a2cos Asin B，‎ 即a2cos Asin B＝b2sin Acos B.‎ 法一：由正弦定理知a＝2Rsin A，b＝2Rsin B，‎ ‎∴sin2Acos Asin B＝sin2Bsin Acos B，‎ 又sin Asin B≠0，∴sin Acos A＝sin Bcos B，‎ ‎∴sin ‎2A＝sin 2B.‎ 在△ABC中，0＜‎2A＜2π，0＜2B＜2π，‎ ‎∴‎2A＝2B或‎2A＝π－2B，‎ ‎∴A＝B或A＋B＝.‎ ‎∴△ABC为等腰三角形或直角三角形．‎ 法二：由正弦定理、余弦定理，得 a2b×＝b‎2a×，‎ ‎∴a2(b2＋c2－a2)＝b2(a2＋c2－b2)，‎ ‎∴(a2－b2)(a2＋b2－c2)＝0，‎ ‎∴a2－b2＝0或a2＋b2－c2＝0.‎ 即a＝b或a2＋b2＝c2.‎ ‎∴△ABC为等腰三角形或直角三角形．‎ 判定三角形形状的三个注意点 ‎(1)“角化边”后要注意用因式分解、配方等方法得出边的关系．‎ ‎(2)“边化角”后要注意用三角恒等变换、三角形内角和定理及诱导公式推出角的关系．‎ ‎(3)要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别．‎ ‎2．在△ABC中，若B＝60°，2b＝a＋c，试判断△ABC的形状．‎ ‎[解]　法一：∵2b＝a＋c，由正弦定理，‎ 得2sin B＝sin A＋sin C.‎ ‎∵B＝60°，∴A＋C＝120°.‎ ‎∴2sin 60°＝sin(120°－C)＋sin C.‎ 展开整理得sin C＋cos C＝1.‎ ‎∴sin(C＋30°)＝1.‎ ‎∵0°2时，如图②，‎ 在△APQ中，AP＝8t，AQ＝10t－20，‎ ‎∴PQ＝ ‎＝2.‎ 综合①②③知，‎ PQ＝2(t≥0)．‎ 当且仅当t＝＝时，PQ最小．‎ 所以甲、乙两船行驶小时后，相距最近．‎ ‎[培优层·素养升华]‎ ‎【例题】　△ABC的内角A，B，C的对边分别为a，b，c.设(sin B－sin C)2＝sin‎2A－sin Bsin C.‎ ‎(1)求A；‎ ‎(2)若a＋b＝‎2c，求sin C.‎ ‎[思路探究]　(1)利用正弦定理结合余弦定理求解角A的大小；‎ ‎(2)根据(1)中的结论结合正弦定理化简题中的等量关系，利用两角差的正弦公式求解sin C.‎ ‎[解]　(1)由已知得sin2B＋sin‎2C－sin‎2A＝sin Bsin C，‎ 故由正弦定理得b2＋c2－a2＝bc.‎ 由余弦定理得cos A＝＝.‎ 因为0°＜A＜180°，所以A＝60°.‎ ‎(2)由(1)知B＝120°－C，‎ 由题设及正弦定理得sin A＋sin(120°－C)＝2sin C，‎ 即＋cos C＋sin C＝2sin C，‎ 整理得cos(C＋60°)＝－.‎ 因为0°＜C＜120°，所以sin(C＋60°)＝，‎ 故sin C＝sin(C＋60°－60°)‎ ‎＝sin(C＋60°)cos 60°－cos(C＋60°)sin 60°‎ ‎＝.‎ 本题考查正弦定理、余弦定理、两角和的余弦公式、两角差的正弦公式，综合性较强.综合应用正、余弦定理解三角形一直是高考的热点内容之一，着重考查直观想象、数学运算等学科素养.‎ ‎△ABC的内角A，B，C的对边分别为a，b，c，已知asin A－bsin B＝4csin C，cos A＝－，则＝(　　)‎ A．6 B．‎5 C．4 D．3‎ A　[∵asin A－bsin B＝4csin C，‎ ‎∴由正弦定理得a2－b2＝‎4c2，即a2＝‎4c2＋b2.‎ 由余弦定理得cos A＝＝＝＝－，∴＝6.]‎