直线和圆的极坐标方程、曲线的极坐标方程与直角坐标方程的互化、 圆锥曲线统一的极坐标方程 练习 3页

直线和圆的极坐标方程、曲线的极坐标方程与直角坐标方程的互化、 圆锥曲线统一的极坐标方程 练习 1 极坐标方程 πcos 4       表示的曲线是( )． A．双曲线 B．椭圆 C．抛物线 D．圆 2 过 A π2, 4      且平行于极轴的直线的极坐标方程是( )． A．ρsin θ＝ 2 B．ρsin θ＝2 C．ρcos θ＝ 2 D．ρcos θ＝2 3 化极坐标方程ρ2cos θ－ρ＝0 为直角坐标方程为( )． A．x2＋y2＝0 或 y＝1 B．x＝1 C．x2＋y2＝0 或 x＝1 D．y＝1 4 圆心在点(－1,1)处，且过原点的圆的极坐标方程是( )． A．ρ＝2(sin θ－cos θ) B．ρ＝2(cos θ－sin θ) C．ρ＝2sin θ D．ρ＝2cos θ 5 过极点 O 作圆 C：ρ＝8cos θ的弦 ON，则 ON 的中点 M 的轨迹方程是__________． 6 已知双曲线的极坐标方程为 3 1 2cos    ，过极点作直线与它交于 A，B 两点，且|AB| ＝6，求直线 AB 的极坐标方程． 7 已知在△ABC 中，AB＝6，AC＝4，当∠A 变化时，求∠A 的平分线与 BC 的中垂线的交 点 P 的轨迹方程． 参考答案 1 答案：D π π π 2 2cos cos cos sin sin cos sin4 4 4 2 2            ＝ ＋ ＋ ，∴ρ2 ＝ 2 2 ρcos θ＋ 2 2 ρsin θ，即 x2＋y2＝ 2 2 2 2x y . 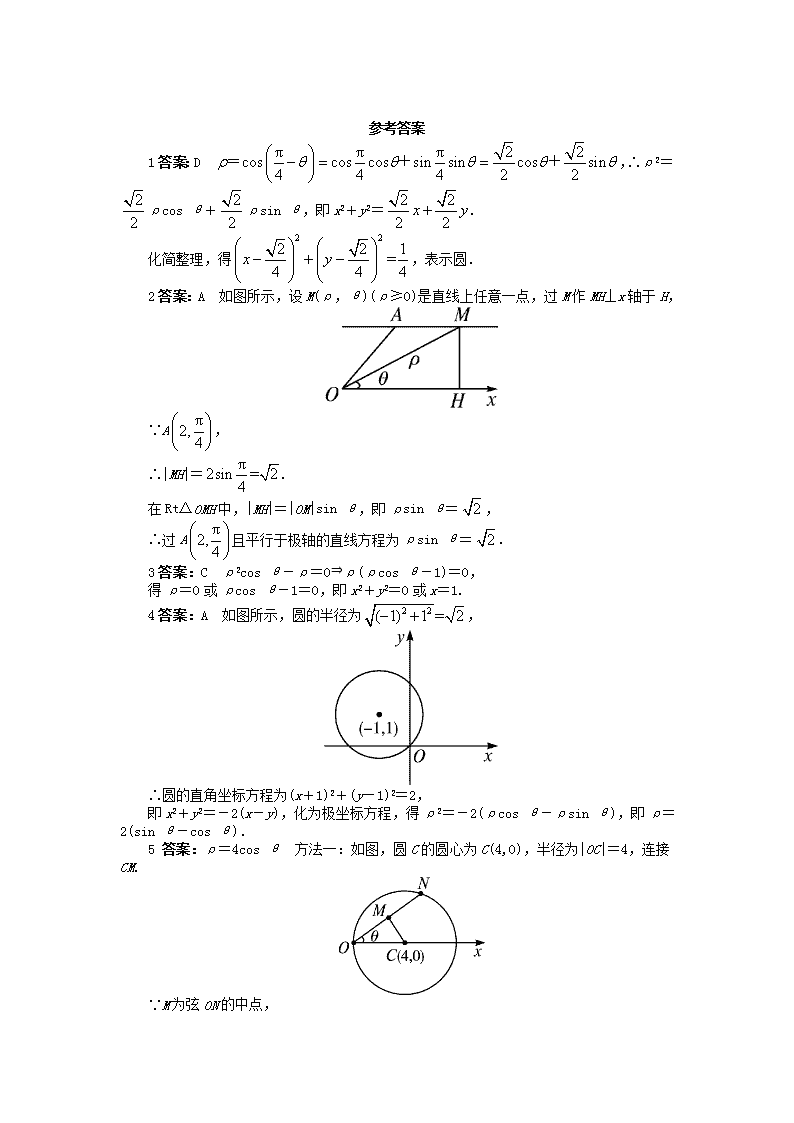化简整理，得 2 2 2 2 1=4 4 4x y                ，表示圆． 2 答案：A 如图所示，设 M(ρ，θ)(ρ≥0)是直线上任意一点，过 M 作 MH⊥x 轴于 H， ∵A π2, 4      ， ∴|MH|＝ π2sin = 24 . 在 Rt△OMH 中，|MH|＝|OM|sin θ，即ρsin θ＝ 2 ， ∴过 A π2, 4      且平行于极轴的直线方程为ρsin θ＝ 2 . 3 答案：C ρ2cos θ－ρ＝0⇒ρ(ρcos θ－1)＝0， 得ρ＝0 或ρcos θ－1＝0，即 x2＋y2＝0 或 x＝1. 4 答案：A 如图所示，圆的半径为 2 21 1 = 2   ， ∴圆的直角坐标方程为(x＋1)2＋(y－1)2＝2， 即 x2＋y2＝－2(x－y)，化为极坐标方程，得ρ2＝－2(ρcos θ－ρsin θ)，即ρ＝2(sin θ－cos θ)． 5 答案：ρ＝4cos θ 方法一：如图，圆 C 的圆心为 C(4,0)，半径为|OC|＝4，连接 CM. ∵M 为弦 ON 的中点， ∴CM⊥ON，故 M 在以 OC 为直径的圆上． ∴点 M 的轨迹方程是ρ＝4cos θ. 方法二：设 M 点的坐标是(ρ，θ)，N(ρ1，θ1)． ∵N 点在圆ρ＝8cos θ上，∴ρ1＝8cos θ1，① ∵M 是 ON 的中点，∴ 1 1 2 , .        将它代入①式得 2ρ＝8cos θ，故点 M 的轨迹方程是ρ＝4cos θ. 6 答案：解：设直线 AB 的极坐标方程为θ＝θ1，A(ρ1，θ1)，B(ρ2，θ1＋π)．则 1 1 3=1 2cos   ， 2 1 1 3 3= =1 2cos π 1 2cos        . |AB|＝|ρ1＋ρ2|＝ 1 1 3 3 1 2cos 1 2cos   2 1 6= 1 4cos  ＝6， ∴ 2 1 1 1 4cos  ＝±1.∴cos θ1＝0 或 cos θ1＝ 2 2  . 故直线 AB 的极坐标方程为 π= 2  或 π= 4  或 3π= 4  . 7 答案：解：取 A 为极点，AB 所在射线为极轴，建立极坐标系， ∵AP 平分∠BAC，MP 为 BC 的中垂线，∴PB＝PC. 设 P(ρ，θ)，(ρ＞0， π π<2 2   且θ≠0)，则 PC2＝AP2＋AC2－2AP·AC·cos θ＝ ρ2＋16－8ρcos θ， PB2＝AP2＋AB2－2AP·ABcos θ＝ρ2＋36－12ρcos θ， ∴ρ2＋16－8ρcos θ＝ρ2＋36－12ρcos θ. 即ρcos θ＝5(ρ＞0， π π<2 2   且θ≠0)． ∴点 P 的轨迹方程为ρcos θ＝5(ρ＞0， π π<2 2   且θ≠0)．