高中数学第三章不等式3-3-2简单的线性规划问题课时作业含解析新人教A版必修5 7页

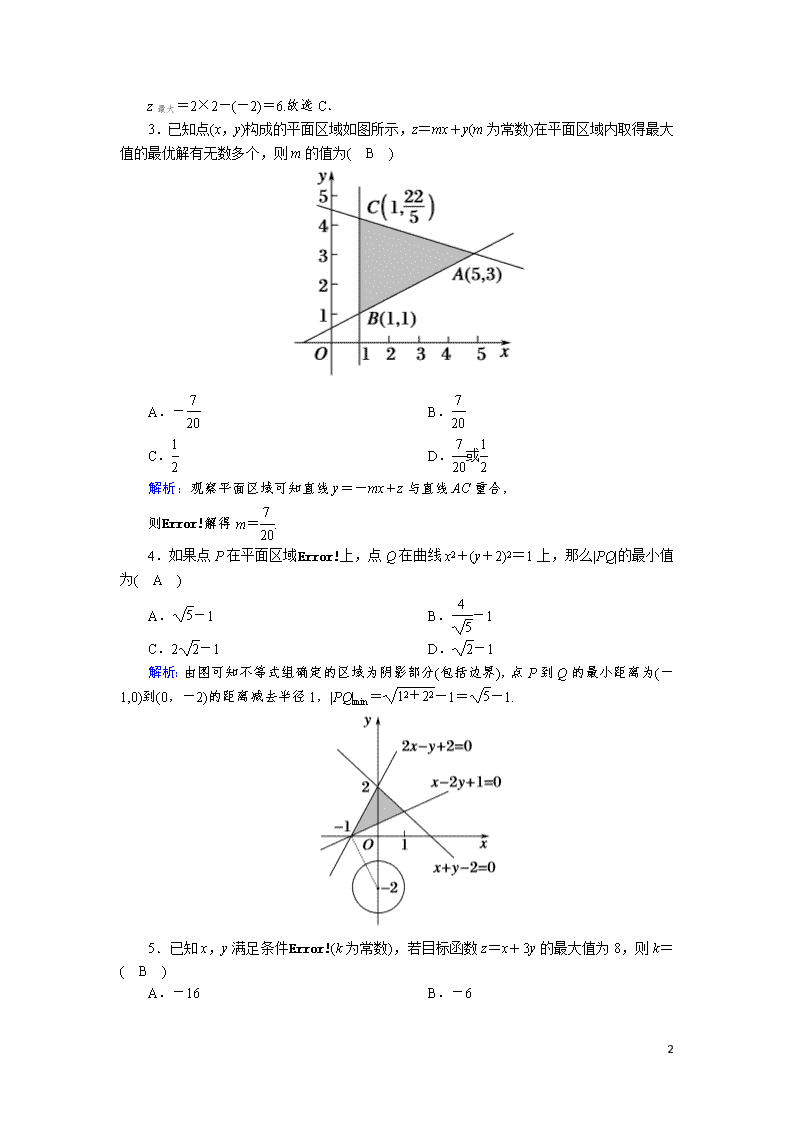
课时作业23　简单的线性规划问题 时间：45分钟 ‎——基础巩固类——‎ 一、选择题 ‎1．设实数x，y满足约束条件则z＝3x－2y的最小值为(　A　)‎ A．－2 B．1‎ C．8 D．13‎ 解析：不等式组表示的可行域如图阴影部分所示．‎ 由z＝3x－2y得y＝x－，平移直线y＝x，‎ 经过A(0,1)时，－最大，此时z最小，‎ z最小＝3×0－2×1＝－2.故选A．‎ ‎2．若点(x，y)在曲线y＝－|x|与y＝－2所围成的封闭区域内(包括边界)，则2x－y的最大值为(　C　)‎ A．－6 B．4‎ C．6 D．8‎ 解析：‎ 如图，点(x，y)在阴影部分区域内，设2x－y＝z，则y＝2x－z，当直线y＝2x－z过点A(2，－2)时－z最小，此时z最大．‎ 7‎ z最大＝2×2－(－2)＝6.故选C．‎ ‎3．已知点(x，y)构成的平面区域如图所示，z＝mx＋y(m为常数)在平面区域内取得最大值的最优解有无数多个，则m的值为(　B　)‎ A．－ B． C． D．或 解析：观察平面区域可知直线y＝－mx＋z与直线AC重合，‎ 则解得m＝.‎ ‎4．如果点P在平面区域上，点Q在曲线x2＋(y＋2)2＝1上，那么|PQ|的最小值为(　A　)‎ A．－1 B．－1‎ C．2－1 D．－1‎ 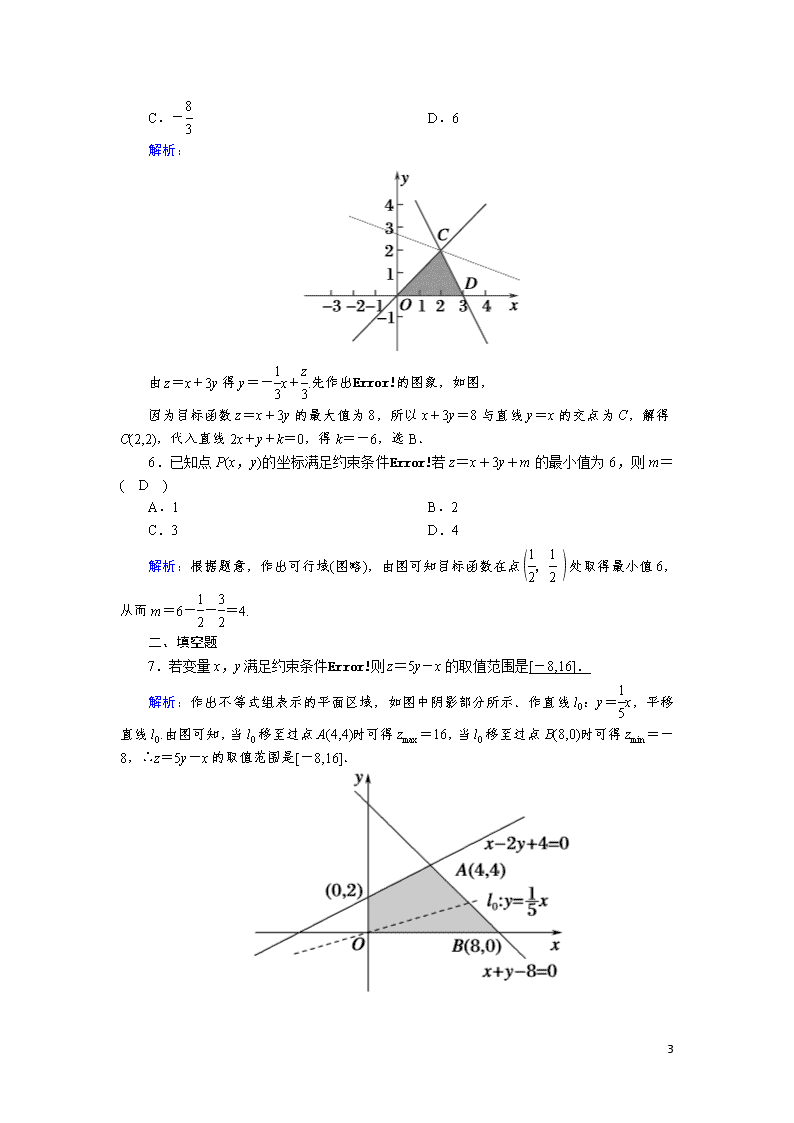解析：由图可知不等式组确定的区域为阴影部分(包括边界)，点P到Q的最小距离为(－1,0)到(0，－2)的距离减去半径1，|PQ|min＝－1＝－1.‎ ‎5．已知x，y满足条件(k为常数)，若目标函数z＝x＋3y的最大值为8，则k＝(　B　)‎ A．－16 B．－6‎ C．－ D．6‎ 7‎ 解析：‎ 由z＝x＋3y得y＝－x＋.先作出的图象，如图，‎ 因为目标函数z＝x＋3y的最大值为8，所以x＋3y＝8与直线y＝x的交点为C，解得C(2,2)，代入直线2x＋y＋k＝0，得k＝－6，选B．‎ ‎6．已知点P(x，y)的坐标满足约束条件若z＝x＋3y＋m的最小值为6，则m＝(　D　)‎ A．1 B．2‎ C．3 D．4‎ 解析：根据题意，作出可行域(图略)，由图可知目标函数在点处取得最小值6，从而m＝6－－＝4.‎ 二、填空题 ‎7．若变量x，y满足约束条件则z＝5y－x的取值范围是[－8,16]．‎ 解析：作出不等式组表示的平面区域，如图中阴影部分所示．作直线l0：y＝x，平移直线l0.由图可知，当l0移至过点A(4,4)时可得zmax＝16，当l0移至过点B(8,0)时可得zmin＝－8，∴z＝5y－x的取值范围是[－8,16]．‎ ‎8．设实数x，y满足则u＝的取值范围是.‎ 解析：‎ 7‎ 作出可行域如图阴影部分所示，由u＝＝＋1，令z＝，表示点(x，y)与原点连线的斜率，由图象数形结合知，zmin＝kOB，zmax＝kOA，‎ 由得点B的坐标为(3,1)．‎ 由得点A的坐标为(1,2)．‎ 则zmin＝，zmax＝2，即∈.‎ 故∈，所以u＝＋1∈.‎ ‎9．已知x，y满足约束条件点A(2,1)，B(x，y)，O为坐标原点，则·最大值时为.‎ 解析：‎ 画出可行域，如图中的阴影部分．已知点A(2,1)，B(x，y)，O为坐标原点，则·＝2x＋y.由图可知，当直线y＝－2x＋z过点C时，z有最大值．解方程组得 故zmax＝2×＋＝.‎ 三、解答题 ‎10．设z＝2y－2x＋4，已知x，y满足条件求z的最大值和最小值．‎ 解：作出满足不等式组的可行域，如图所示的阴影部分．‎ 7‎ 作直线l：2y－2x＝t.‎ 当l经过点A(0,2)时，zmax＝2×2－2×0＋4＝8；‎ 当l经过点B(1,1)时，zmin＝2×1－2×1＋4＝4.‎ ‎11．设x，y满足条件 ‎(1)求v＝的最大值与最小值；‎ ‎(2)求u＝x2＋y2的最大值与最小值．‎ 解：画出满足条件的可行域如图所示，‎ ‎(1)v＝表示可行域内的点P(x，y)与定点D(5,0)的斜率，由图可知，kBD最大，kCD最小，又C(3,8)，B(3，－3)，‎ 所以vmax＝＝，vmin＝＝－4.‎ ‎(2)x2＋y2＝u表示一组同心圆(圆心为原点O)，且对同一圆上的点x2＋y2的值都相等，由图可知：当(x，y)在可行域内取值时，当且仅当圆O过C点时，u最大，过(0,0)时，u最小，点C坐标为(3,8)，‎ 所以umax＝73，umin＝0.‎ ‎——能力提升类——‎ ‎12．设z＝x＋y，其中实数x，y满足若z的最大值为6，则z的最小值为(　A　)‎ A．－3 B．－2‎ C．－1 D．0‎ 7‎ 解析：作出不等式组对应的平面区域如图中阴影部分所示，由z＝x＋y，得y＝－x＋z，由图可知当直线y＝－x＋z经过点A时，直线y＝－x＋z在y轴上的截距最大，此时z最大为6，由得即点A(k，k)，∴z＝k＋k＝6，得k＝3.当直线y＝－x＋z经过点B时，z取得最小值，由解得即点B(－6,3)，此时z的最小值为－6＋3＝－3.‎ ‎13．已知变量x，y满足约束条件若x＋2y≥－5恒成立，则实数a的取值范围为(　C　)‎ A．(－∞，－1] B．[－1，＋∞)‎ C．[－1,1] D．[－1,1)‎ 解析：由题意作出可行域，如图所示，由图易知a≤1，x＋2y≥－5恒成立可化为图中的阴影部分恒在直线x＋2y＝－5的右上方，即点A在直线x＋2y＝－5上或其右上方，易知A点坐标为(a，a－1)，所以a＋2(a－1)≥－5，所以实数a的取值范围为[－1,1]．‎ ‎14．若x，y满足x＋1≤y≤2x，则2y－x的最小值是3.‎ 解析：‎ 7‎ 作出不等式组 所表示的平面区域如图中阴影部分所示，令z＝2y－x，作出直线2y－x＝0，平移该直线，当直线过点A(1,2)时，2y－x取得最小值，最小值为2×2－1＝3.‎ ‎15．某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元．甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别是0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？‎ 解：设公司在甲、乙两个电视台做广告的时间分别是x分钟、y分钟，总收益为z万元，由题意得：‎ 目标函数为z＝3 000x＋2 000y.‎ 作出二元一次不等式组所表示的区域，即可行域，如图阴影部分所示：‎ 作直线l即3x＋2y＝0.平移直线l，从图中可知，当直线l过点M时，目标函数取得最大值．‎ 由解得 即M(100,200)．‎ 则zmax＝3 000x＋2 000y＝700 000(元)，‎ 即该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司收益最大，最大收益是70万元．‎ 7‎