高中数学必修2立体几何解答题含答案 13页

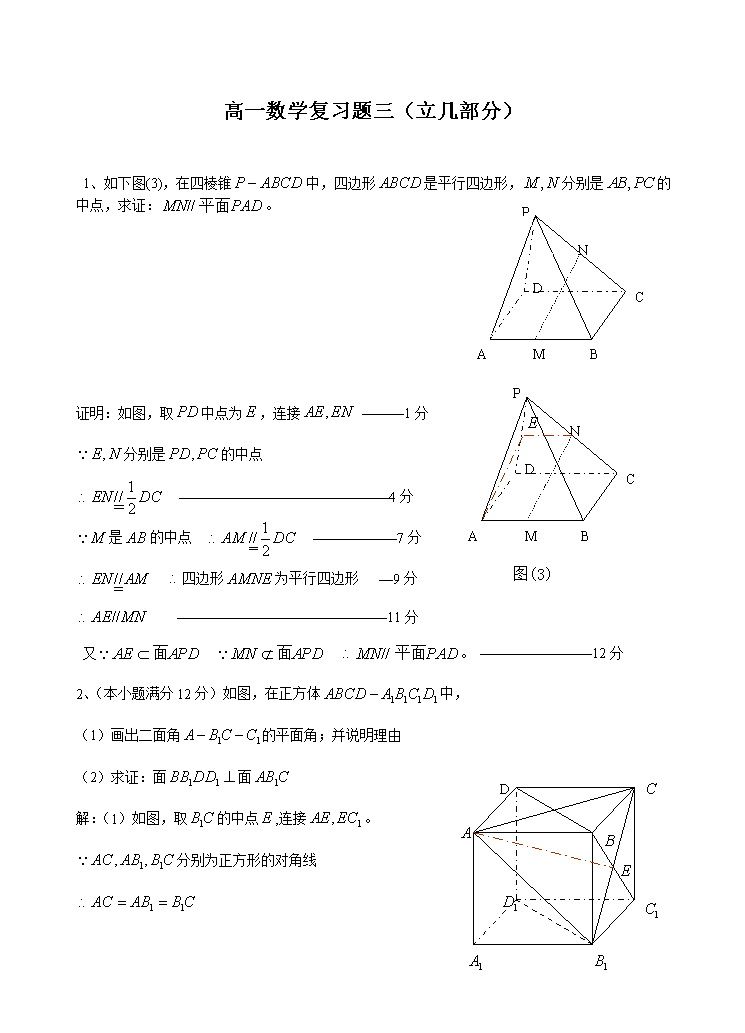
高一数学复习题三（立几部分） 1、如下图(3)，在四棱锥 P ABCD 中，四边形 ABCD 是平行四边形， ,M N 分别是 ,AB PC 的 中点，求证： MN PAD// 平面 。 证明：如图，取 PD 中点为 E ，连接 ,AE EN ———1 分 ,E N 分别是 ,PD PC 的中点 1 2EN DC // ———————————————4 分 M 是 AB 的中点 1 2AM DC // ——————7 分 EN AM // 四边形 AMNE 为平行四边形 —9 分 AE MN // ———————————————11 分 又 AE APD 面 MN APD 面  MN PAD// 平面 。 ————————12 分 2、（本小题满分 12 分）如图，在正方体 1 1 1 1ABCD A B C D 中， （1）画出二面角 1 1A B C C  的平面角；并说明理由 （2）求证：面 1 1BB DD  面 1AB C 解：（1）如图，取 1B C 的中点 E ,连接 1,AE EC 。 1 1, ,AC AB B C 分别为正方形的对角线 1 1AC AB B C   E 是 1B C 的中点 B C A D M N P 图(3) E 1A 1B 1D 1C C A B D D E B C A D M N P 1AE B C  ——————————————2 分 又在正方形 1 1BB C C 中 1 1EC B C  ——————————————3 分  1AEC 为二面角 1 1A B C C  的平面角。 —————————————————4 分 （2） 证明： 1D D ABCD 面 ， AC ABCD 面 1D D AC  —————6 分 又在正方形 ABCD 中 AC BD  —————————————————8 分 1D D BD D  1 1AC DD B B  面 ———————————————10 分 又 1AC AB C 面 面 1 1BB DD  面 1AB C ——————————————12 分 3、如图，在边长为 a 的菱形 ABCD 中，E,F 是 PA 和 AB 的中点。∠ABC=60°，PC⊥面 ABCD； （1）求证： EF||平面 PBC ; （2）求 E 到平面 PBC 的距离。 解（1）证明： PBEF BFAFPEAE || ,,   又 ,, PBCPBPBCEF 平面平面  故 PBCEF 平面|| （2）解：在面 ABCD 内作过 F 作 HBCFH 于 PBCPCABCDPC 面面  , ABCDPBC 面面  A B CD P E F 又 BCABCDPBC 面面  ， BCFH  ， ABCDFH 面 ABCDFH 面 又 PBCEF 平面|| ，故点 E 到平面 PBC 的距离等于点 F 到平面 PBC 的距离 FH。 在直角三角形 FBH 中， 2 ,60 aFBFBC   ， aaaFBCFBFH 4 3 2 3 260sin2sin 0  故点 E 到平面 PBC 的距离等于点 F 到平面 PBC 的距离， 等于 a4 3 4、（本题８分）如图，四棱锥 S- ABCD 中，底面 ABCD 为 平 行 四 边形，E 是 SA 上一点， 试探求点 E 的位置，使 SC//平面 EBD，并证明． 答：点 E 的位置是 ． 证明： 解：答：点 E 的位置是 棱 SA 的中点 ． 证明：取 SA 的中点 E，连结 EB，ED，AC，设 AC 与 BD 的 交 点 为 O，连结 EO． ∵四边形 ABCD 是平行四边形， ∴点 O 是 AC 的中点． 又 E 是 SA 的中点，∴OE 是ΔSAC 的中位线． ∴OE//SC． ∵SC  平面 EBD，OE  平面 EBD， ∴SC//平面 EBD． 5、（本题 10 分）如图，已知正方体 ABCD-A1B1C1D1，AD1 与 A1D 相交 于点 O． （1）判断 AD1 与平面 A1B1CD 的位置关系，并证明； （2）求直线 AB1 与平面 A1B1CD 所成的角． (1)解： CDBAAD 111 平面 ． 证明：∵在正方体 ABCD-A1B1C1D1 中， O B 1 D 1 C A 1 D C 1 B A 题 23 图 B C D A S 题 20 图 ,, 11111 DAADADBA  1111 ABADA  ， ∴ CDBAAD 111 平面 ． （2）连结 OB1 ．∵ CDBAAD 111 平面 于点 O， ∴直线 OB1 是直线 1AB 在平面 CDBA 11 上的射影．m ∴ OAB1 为直线 1AB 与平面 CDBA 11 所成的角． 又∵ AOAB 21  ， ∴ 2 1sin 1 1  AB AOOAB ． ∴ 301  OAB °． 6、如图，用一付直角三角板拼成一直二面角 A—BD—C，若其中给定 AB=AD =2，  90BCD ，  60BDC ， （Ⅰ）求三棱锥 A-BCD 的体积； （Ⅱ）求直线 AC 与平面 BCD 所成角的大小； （Ⅲ）求点 D 到平面 ABC 的距离． 解：(1)、∵二面角 A-BD-C 是直二面角 ∴平面 ABD⊥平面 CBD 过 A 作 AE⊥BD，垂足为 E，则 AE⊥面 ABD 即 AE 是三棱锥 A-BCD 的高 又 由已知得：BD= 2 2 ，DC= 1 2 BD= 2 ，BC= 2 2 6BD CD  ,AE= 2 ∴  BCD 的面积为 BCDS  3 ∴三棱锥 A-BCD 的体积为 6 3A BCDV   （2）、∵AE⊥面 ABD 所以 CE 为直线 AC 在平面 BCD 内的射影， ACE 为直线 AC 与平面 BCD 所成的角， 在 Rt AEC 中， 2AE , 22 1  BDCE ， 45ACE   ， 故直线 AC 与平面 BCD 所成的角为 45 （3）、过 E 作 EF⊥BC，垂足为 F，连接 AF，则 AF⊥BC. A DB C 又在 Rt△AEF 中可求得 AF= 10 2 ∴ ABCS  15 2 设点 D 到平面 ABC 的距离为 h A BCD D ABCV V  1 6 3 3A BCDABCh S V      2 0 5 3 1A BCD ABC Vh S     即 D 到面 ABC 的距离为 2 10= 5h 注意：利用等体积积法求点到面的距离。 7、如图,在直三棱柱 1 1 1ABC ABC 中, 3AC  , 4BC  , 5AB  , 点 D 是 AB 的中点. (1)求证: 1AC BC ; (2)求证: 1AC ∥平面 1CDB . 证明: (1) 因为三棱柱 1 1 1ABC A B C 为直三棱柱, 所以 1C C  平面 ABC , 所以 1C C AC . 又因为 3AC  , 4BC  , 5AB  , 所以 2 2 2AC BC AB  , 所以 AC BC . 又 1CC BC C  , 所以 AC  平面 1 1CC B B , 所以 1AC BC . (2) 令 1BC 与 1CB 的交点为 E , 连结 DE . 因为 D 是 AB 的中点, E 为 1BC 的中点, D A 1 B 1 C B A C 1 （第 6 题图） 所以 DE ∥ 1AC . 又 因为 1AC  平面 1CDB , DE  平面 1CDB , 所以 1AC ∥平面 1CDB . 8、（本小题 14 分）已知四棱锥 P-ABCD，底面 ABCD 是 60A 、边长为 a 的菱形，又 ABCDPD 底 ，且 PD=CD，点 M、N 分别是棱 AD、PC 的中点． （1）证明：DN//平面 PMB； （2）证明：平面 PMB  平面 PAD； （3）求点 A 到平面 PMB 的距离． 解：（1）证明：取 PB 中点 Q，连结 MQ、NQ，因为 M、N 分别是棱 AD、PC 中点，所以 QN//BC//MD，且 QN=MD，于是 DN//MQ. PMBDN PMBDN PMBMQ MQDN 平面 平面 平面 // //       . … …………………6 分 （2） MBPD ABCDMB ABCDPD       平面 平面 又因为底面 ABCD 是 60A 、边长为 a 的菱形，且 M 为 AD 中点， 所以 ADMB  .又 所以 PADMB 平面 . .PADPMB PMBMB PADMB 平面平面 平面 平面       ………………10 分 （3）因为 M 是 AD 中点，所以点 A 与 D 到平面 PMB 等距离. 过点 D 作 PMDH  于 H，由（2）平面 PMB  平面 PAD，所以 PMBDH 平面 . N M B P D C A 故 DH 是点 D 到平面 PMB 的距离. .5 5 2 5 2 a a aa DH    所以点 A 到平面 PMB 的距离为 a5 5 .………14 分 答案打印 1、证明：如图，取 PD 中点为 E ，连接 ,AE EN ———1 分 ,E N 分别是 ,PD PC 的中点 1 2EN DC // —————————4 分 M 是 AB 的中点 1 2AM DC // ———7 分 EN AM // 四边形 AMNE 为平行四边形 —9 分 AE MN // ———————————————11 分 又 AE APD 面 MN APD 面  MN PAD// 平面 。 ————————12 分 2、解：（1）如图，取 1B C 的中点 E ,连接 1,AE EC 。 1 1, ,AC AB B C 分别为正方形的对角线 1 1AC AB B C   E 是 1B C 的中点 1AE B C  ——————————————2 分 又在正方形 1 1BB C C 中 1 1EC B C  ——————————————3 分  1AEC 为二面角 1 1A B C C  的平面角。 —————————————————4 分 （2） 证明： 1D D ABCD 面 ， AC ABCD 面 1D D AC  —————6 分 又在正方形 ABCD 中 AC BD  —————————————————8 分 1D D BD D  1 1AC DD B B  面 ———————————————10 分 1A 1B 1D 1C C A B D D E 又 1AC AB C 面 面 1 1BB DD  面 1AB C ——————————————12 分 3、 解（1）证明： PBEF BFAFPEAE || ,,   又 ,, PBCPBPBCEF 平面平面  故 PBCEF 平面|| （2）解：在面 ABCD 内作过 F 作 HBCFH 于 PBCPCABCDPC 面面  , ABCDPBC 面面  又 BCABCDPBC 面面  ， BCFH  ， ABCDFH 面 ABCDFH 面 又 PBCEF 平面|| ，故点 E 到平面 PBC 的距离等于点 F 到平面 PBC 的距离 FH。 在直角三角形 FBH 中， 2 ,60 aFBFBC   ， aaaFBCFBFH 4 3 2 3 260sin2sin 0  故点 E 到平面 PBC 的距离等于点 F 到平面 PBC 的距离， 等于 a4 3 4、解：答：点 E 的位置是 棱 SA 的中点 ． 证明：取 SA 的中点 E，连结 EB，ED，AC，设 AC 与 BD 的交点为 O， 连结 EO． ∵四边形 ABCD 是平行四边形， ∴点 O 是 AC 的中点． 又 E 是 SA 的中点，∴OE 是ΔSAC 的中位线． ∴OE//SC． ∵SC  平面 EBD，OE  平面 EBD， ∴SC//平面 EBD． 5、(1)解： CDBAAD 111 平面 ． O B 1 D 1 C A 1 D C 1 B A B C D A S 证明：∵在正方体 ABCD-A1B1C1D1 中， ,, 11111 DAADADBA  1111 ABADA  ， ∴ CDBAAD 111 平面 ． （2）连结 OB1 ．∵ CDBAAD 111 平面 于点 O， ∴直线 OB1 是直线 1AB 在平面 CDBA 11 上的射影．m ∴ OAB1 为直线 1AB 与平面 CDBA 11 所成的角． 又∵ AOAB 21  ， ∴ 2 1sin 1 1  AB AOOAB ． ∴ 301  OAB °． 6、解：(1)、∵二面角 A-BD-C 是直二面角 ∴平面 ABD⊥平面 CBD 过 A 作 AE⊥BD，垂足为 E，则 AE⊥面 ABD 即 AE 是三棱锥 A-BCD 的高 又 由已知得：BD= 2 2 ，DC= 1 2 BD= 2 ， BC= 2 2 6BD CD  ,AE= 2 ∴  BCD 的面积为 BCDS  3 ∴三棱锥 A-BCD 的体积为 6 3A BCDV   （2）、∵AE⊥面 ABD 所以 CE 为直线 AC 在平面 BCD 内的射影， ACE 为直线 AC 与平面 BCD 所成的角， 在 Rt AEC 中， 2AE , 22 1  BDCE ， 45ACE   ， 故直线 AC 与平面 BCD 所成的角为 45 （3）、过 E 作 EF⊥BC，垂足为 F，连接 AF，则 AF⊥BC. 又在 Rt△AEF 中可求得 AF= 10 2 A DB C ∴ ABCS  15 2 设点 D 到平面 ABC 的距离为 h A BCD D ABCV V  1 6 3 3A BCDABCh S V      2 0 5 3 1A BCD ABC Vh S     即 D 到面 ABC 的距离为 2 10= 5h 注意：利用等体积积法求点到面的距离。 7、证明: (1) 因为三棱柱 1 1 1ABC A B C 为直三棱柱, 所以 1C C  平面 ABC , 所以 1C C AC . 又因为 3AC  , 4BC  , 5AB  , 所以 2 2 2AC BC AB  , 所以 AC BC . 又 1CC BC C  , 所以 AC  平面 1 1CC B B , 所以 1AC BC . (2) 令 1BC 与 1CB 的交点为 E , 连结 DE . 因为 D 是 AB 的中点, E 为 1BC 的中点, 所以 DE ∥ 1AC . 又 因为 1AC  平面 1CDB , DE  平面 1CDB , 所以 1AC ∥平面 1CDB . D A 1 B 1 C B A C 1 （第 7 题图） 高一数学复习题一（立几部分） 姓名 考号 1、（本小题满分 12 分）如下图(3)，在四棱锥 P ABCD 中， 四边形 ABCD 是平行四边形， ,M N 分别是 ,AB PC 的中 点， 求证： MN PAD// 平面 。 2、（本小题满分 12 分）如图，在正方体 1 1 1 1ABCD A B C D 中， （2）画出二面角 1 1A B C C  的平面角；并说明理由 （2）求证：面 1 1BB DD  面 1AB C 3、如图，在边长为 a 的菱形 ABCD 中，E,F 是 PA 和 AB 的中点。∠ABC=60°，PC⊥面 ABCD； （1）求证： EF||平面 PBC ; （2）求 E 到平面 PBC 的距离。 1A 1B 1D 1C C A B D E CD P E B C A D M N P 4、（本题８分）如图，四棱锥 S- ABCD 中，底面 ABCD 为平行四边形，E 是 SA 上一点， 试探求点 E 的位置，使 SC//平面 EBD，并证明． 答：点 E 的位置是 ． 证明： 5、（本题 10 分）如图，已知正方体 ABCD-A1B1C1D1，AD1 与 A1D 相交于点 O． （1）判断 AD1 与平面 A1B1CD 的位置关系，并证明； （2）求直线 AB1 与平面 A1B1CD 所成的角． 6、如图，用一付直角三角板拼成一直二面角 A—BD—C，若其中给定 AB=AD =2，  90BCD ，  60BDC ， （Ⅰ）求三棱锥Ａ－BCD 的体积； （Ⅱ）求直线 AC 与平面 BCD 所成角的大小； （Ⅲ）求点 D 到平面 ABC 的距离． 7、如图,在直三棱柱 1 1 1ABC ABC 中, 3AC  , 4BC  , 5AB  , 点 D 是 AB 的中点. O B 1 D 1 C A 1 D C 1 B A 题 5 图 B C D A S 题 4 图 D A 1 B 1 C B A C 1 A DB C (1)求证: 1AC BC ; (2)求证: 1AC ∥平面 1CDB .