- 399.38 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
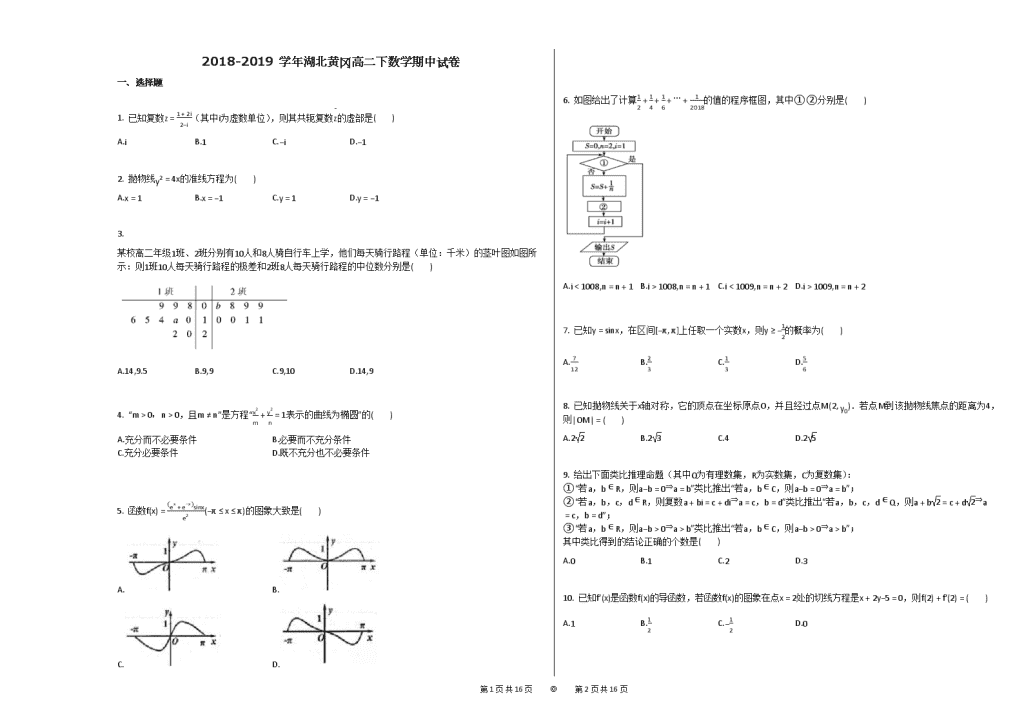
2018-2019学年湖北黄冈高二下数学期中试卷
一、选择题
1. 已知复数z=1+2i2−i(其中i为虚数单位),则其共轭复数z¯的虚部是( )
A.i B.1 C.−i D.−1
2. 抛物线y2=4x的准线方程为( )
A.x=1 B.x=−1 C.y=1 D.y=−1
3.
某校高二年级1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
A.14,9.5 B.9,9 C.9,10 D.14,9
4. “m>0,n>0,且m≠n”是方程“x2m+y2n=1表示的曲线为椭圆”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5. 函数f(x)=ex+e−xsinxe2(−π≤x≤π)的图象大致是( )
A. B.
C. D.
6. 如图给出了计算12+14+16+⋯+12018的值的程序框图,其中①②分别是( )
A.i<1008,n=n+1 B.i>1008,n=n+1 C.i<1009,n=n+2 D.i>1009,n=n+2
7. 已知y=sinx,在区间[−π, π]上任取一个实数x,则y≥−12的概率为( )
A.712 B.23 C.13 D.56
8. 已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2, y0).若点M到该抛物线焦点的距离为4,则|OM|=( )
A.22 B.23 C.4 D.25
9. 给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a−b=0⇒a=b”类比推出“若a,b∈C,则a−b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b2=c+d2⇒a=c,b=d”;
③“若a,b∈R,则a−b>0⇒a>b”类比推出“若a,b∈C,则a−b>0⇒a>b”;
其中类比得到的结论正确的个数是( )
A.0 B.1 C.2 D.3
10. 已知f′(x)是函数f(x)的导函数,若函数f(x)的图象在点x=2处的切线方程是x+2y−5=0,则f(2)+f′(2)=( )
A.1 B.12 C.−12 D.0
第13页 共16页 ◎ 第14页 共16页
11. 已知F1,F2是椭圆x2a2+y2b2=1(a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在椭圆C上,则椭圆C的离心率是( )
A.12 B.13 C.3−1 D.4−23
12. 设直线x=t与函数f(x)=2x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为( )
A.1 B.12 C.52 D.22
二、解答题
已知p:∀m∈[−1,1],a2−5a−3≥m2+8;q:∃x∈R,x2+ax+2<0成立.若p为真而q为假,求a的取值范围.
设Z1是虚数,Z2=Z1+2Z1是实数,且−1≤Z2≤2.
(1)求|Z1|的值以及Z1的实部的取值范围;
(2)若ω=2−Z12+Z1,求证ω为纯虚数.
已知a是实数,函数f(x)=x2(x−a).求f(x)在区间[−1, 0]上的最大值.
某地区工会利用“健步行APP”开展健步走积分奖励活动.会员每天走5千步可获积分30分(不足5千步不积分),每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了1000名会员,统计了当天他们的步数,并将样本数据分为[3, 5),[5, 7),[7, 9),[9, 11),[11, 13),[13, 15),[15, 17),[17, 19),[19, 21]九组,整理得到如下频率分布直方图:
(1)从当天步数在[11, 13),[13, 15),[15, 17)的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于220分的概率;
(2)求该组数据的中位数.
如图,已知定点D(2,0),点P是圆C:(x+2)2+y2=36上任意一点,线段PD的垂直平分线与半径CP相交于点M.
(1)当点P在圆上运动时,求点M的轨迹方程
(2)过定点Q(0,1)且斜率为k的直线l与M的轨迹交于A,B两点,若OA→⋅OB→=−6,求点O到直线l的距离.
已知f(x)=x−ax−(a+1)lnx.
(1)当a=−1时,以P2,52为切点作曲线y=f(x)的切线,求切线的方程;
(2)若存在x0∈(0,+∞),使fx0>x0成立,求a的取值范围.
第13页 共16页 ◎ 第14页 共16页
参考答案与试题解析
2018-2019学年湖北黄冈高二下数学期中试卷
一、选择题
1.
【答案】
D
【考点】
复数代数形式的乘除运算
复数的基本概念
【解析】
先将复数z+iz化简为代数形式,再根据复数实部的概念作答
【解答】
解:z=1+2i2−i=(1+2i)(2+i)(2−i)(2+i)
=5i5=i.
∴ 其共轭复数z¯=−i,
故虚部是−1.
故选D.
2.
【答案】
B
【考点】
抛物线的性质
【解析】
此题暂无解析
【解答】
解:由抛物线的性质可得y2=4x的准线方程为x=−1.
故选B.
3.
【答案】
A
【考点】
极差、方差与标准差
众数、中位数、平均数
【解析】
此题暂无解析
【解答】
解:由图可得:
1班的极差为:22−8=14,
2班的中位数为:9+102=9.5.
故选A.
4.
【答案】
C
【考点】
椭圆的定义
必要条件、充分条件与充要条件的判断
【解析】
m>n>0,显然方程x2m2+y2n2=1表示椭圆;方程x2m2+y2n2=1表示椭圆不能推出m>n>0,从而得知正确答案.
【解答】
解:若m>0,n>0,且m≠n,则方程x2m+y2n=1表示椭圆,前者是后者的充分条件;
方程x2m+y2n=1表示椭圆,只需m>0,n>0,且m≠n即可,后者能推出前者,
故前者是后者的充分必要条件.
故选C.
5.
【答案】
A
【考点】
函数奇偶性的性质
函数的图象
【解析】
此题暂无解析
【解答】
解:因为f(x)为奇函数,所以选项B错误;
又fπ2=ex2+e−π2sinπ2e2=eπ2+e−π2e2>0,所以选项D错误;
f′π2=eπ2−e−π2sinπ2+eπ2+e−π2cosπ2e2>0,所以选项C错误.
故选A.
6.
【答案】
D
【考点】
程序框图
【解析】
第13页 共16页 ◎ 第14页 共16页
此题暂无解析
【解答】
解:∵ i的初始为1,每进行一次加法i+1,
根据所要计算内容的规律,得知共进行1008次之后i符合①处的条件,
∴ ①处应该是i>1009,
②处应为n=n+2.
故选D.
7.
【答案】
B
【考点】
正弦函数的单调性
几何概型计算(与长度、角度、面积、体积有关的几何概型)
【解析】
根据题意先确定是几何概型中的长度类型,由“此数小于1“求出构成的区域长度,再求出在区间[0, 3]上任取一个数x构成的区域长度,再求两长度的比值.
【解答】
解:当x∈[−5π6,−π6]时,y≤−12,
此时P=−π6+5π62π=13.
∴ y≥−12的概率为1−13=23.
故选B.
8.
【答案】
D
【考点】
抛物线的求解
椭圆的标准方程
【解析】
关键点M(2, y0)到该抛物线焦点的距离为3,利用抛物线的定义,可求抛物线方程,进而可得点M的坐标,由此可求|OM|.
【解答】
解:由题意,抛物线关于x轴对称,开口向右,设方程为y2=2px(p>0)
∵ 点M(2, y0)到该抛物线焦点的距离为4,
∴ 2+p2=4,
∴ p=4,
∴ 抛物线方程为y2=8x,
∵ M(2, y0),
∴ y02=16,
∴ |OM|=4+16=25.
故选D.
9.
【答案】
C
【考点】
类比推理
【解析】
在数集的扩展过程中,有些性质是可以传递的,但有些性质不能传递,因此,要判断类比的结果是否正确,关键是要在新的数集里进行论证,要想证明一个结论是错误的,也可直接举一个反例.
【解答】
解:①在复数集C中,若两个复数满足a−b=0,则它们的实部和虚部均相等,则a,b相等.故①正确;
②在有理数集Q中,由a+b2=c+d2得,(a−c)+2(b−d)=0,易得:a=c,b=d.故②正确;
③在复数范围内,a−b>0不能推出a>b,比如a=2+i,b=1+i,显然有a−b=1>0成立,但a,b不能比较大小,故③错误.
故选C.
10.
【答案】
A
【考点】
利用导数研究曲线上某点切线方程
【解析】
由导数的几何意义求出该点处切线的导数以及该点处的函数值,代入求值即可
【解答】
解:由题意函数f(x)的图象在点x=2处的切线方程是x+2y−5=0,
f′(2)=−12,f(2)=32.
故f(2)+f′(2)=1
故选A.
11.
【答案】
C
【考点】
椭圆的离心率
椭圆的定义
【解析】
设边PF1的中点为Q,连接F2Q,Rt△QF1F2中,算出|QF1|=c且|QF2|=3c,根据椭圆的定义得2a=|QF1|+|QF2|=(1+3)c,由此不难算出该椭圆的离心率.
【解答】
解:由题意,设边MF1的中点为Q,连接F2Q,
在△QF1F2
第13页 共16页 ◎ 第14页 共16页
中,∠QF1F2=60∘,∠QF2F1=30∘
Rt△QF1F2中,|F1F2|=2c(椭圆的焦距),
∴ |QF1|=12|F1F2|=c,|QF2|=32|F1F2|=3c,
根据椭圆的定义,得2a=|QF1|+|QF2|=(1+3)c,
∴ 椭圆的离心率为e=ca=2c(1+3)c=3−1,
故选C.
12.
【答案】
B
【考点】
导数在最大值、最小值问题中的应用
【解析】
将两个函数作差,得到函数y=f(x)−g(x),再求此函数的最小值对应的自变量x的值.
【解答】
解:设函数y=f(x)−g(x)=2x2−lnx,求导数得
y′=4x−1x=4x2−1x.
当012时,y′>0,函数在(12,+∞)上为单调增函数
所以当x=12时,所设函数的最小值为12−ln12.
所求t的值为12.
故选B.
二、解答题
【答案】
解:若p成立,由m∈[−1, 1]得m2+8∈[22,3],
即a2−5a−3≥3,解得a≥6或a≤−1;
若q成立,则不等式中Δ>0,解得a>22或a<−22;
若p真q假,则−22≤a≤−1.
【考点】
复合命题及其真假判断
一元二次不等式的解法
【解析】
分别求出命题p和q中m的范围和a的范围,若“p或q”为真,“p且q”为假,可知命题p与q一真一假,从而求出a的取值范围;
【解答】
解:若p成立,由m∈[−1, 1]得m2+8∈[22,3],
即a2−5a−3≥3,解得a≥6或a≤−1;
若q成立,则不等式中Δ>0,解得a>22或a<−22;
若p真q假,则−22≤a≤−1.
【答案】
(1)解:设Z1=a+bi,(a,b∈R,且b≠0),
则Z2=Z1+2Z1=a+bi+2a+bi
=(a+2aa2+b2)+(b−2ba2+b2)i,
∵ Z2是实数,b≠0,∴ a2+b2=2,即|Z1|=2,且Z2=2a,
由−1≤Z2≤2,得−1≤2a≤2,解得−12≤a≤1,
即Z1的实部的取值范围为[−12, 1].
(2)证明:ω=2−Z12+Z1=2−a−bi2+a+bi
=2−a2−b2−22bi(2+a)2+b2=−ba+2i,
∵ a∈[−12, 1],b≠0,
∴ −ba+2≠0,
故ω是纯虚数.
【考点】
复数的模
复数代数形式的乘除运算
复数的基本概念
【解析】
(1)设z1=a+bi,(a,b∈R,且b≠0),则z2=z1+1z1=(a+aa2+b2)+(b−ba2+b2),由z1是实数,得a2+b2=1,由此求出z1的实部的取值范围为[−12, 12].
(2)ω=1−Z11+Z1=1−a−bi1+a+bi=1−a2−b2−2bi(1+a)2+b2=ba+1i,由此能证明ω=1−Z11+Z1是纯虚数.
【解答】
(1)解:设Z1=a+bi,(a,b∈R,且b≠0),
则Z2=Z1+2Z1=a+bi+2a+bi
=(a+2aa2+b2)+(b−2ba2+b2)i,
∵ Z2是实数,b≠0,∴ a2+b2=2,即|Z1|=2,且Z2=2a,
由−1≤Z2≤2,得−1≤2a≤2,解得−12≤a≤1,
即Z1的实部的取值范围为[−12, 1].
(2)证明:ω=2−Z12+Z1=2−a−bi2+a+bi
=2−a2−b2−22bi(2+a)2+b2=−ba+2i,
∵
第13页 共16页 ◎ 第14页 共16页
a∈[−12, 1],b≠0,
∴ −ba+2≠0,
故ω是纯虚数.
【答案】
解:令f′(x)=0,
解得x1=0,x2=2a3.
①当2a3≥0,即a≥0时,f(x)在[−1, 0]上单调递增,
从而f(x)max=f(0)=0.
②当2a3≤−1时,即a≤−32时,f(x)在[−1, 0]上单调递减,
从而f(x)max=f(−1)=−1−a.
③当−1<2a3<0,即−32x0成立,
所以存在x0∈(0,+∞),使a+(a+1)x0lnx0<0成立,
令g(x)=a+(a+1)xlnx,
则g′(x)=(a+1)(lnx+1).
①若(a+1)>0,
则x∈0,1e时,g′(x)<0,
g(x)为减函数;
x∈1e,+∞时,g′(x)>0,
g(x)为增函数.
所以当x=1e时,
g(x)min=a+(a+1)1eln1e=a(e−1)−1e.
由a(e−1)−1e<0,a+1>0,
得−11时,有g(x)<0恒成立,即存在x0∈(0,+∞),
使a+(a+1)x0lnx0<0,
综上,a的取值范围是−∞,1e−1.
【考点】
利用导数研究不等式恒成立问题
利用导数研究曲线上某点切线方程
利用导数研究函数的单调性
【解析】
此题暂无解析
【解答】
解:(1)因为a=−1,
所以f(x)=x+1x, f′(x)=1−1x2.
则f′(2)=1−14=34.
则切线方程为y=34(x−2)+52=34x+1.
所以切线方程为3x−4y+4=0.
(2)因为存在x0∈(0,+∞),使fx0>x0成立,
所以存在x0∈(0,+∞),使a+(a+1)x0lnx0<0成立,
令g(x)=a+(a+1)xlnx,
则g′(x)=(a+1)(lnx+1).
①若(a+1)>0,
则x∈0,1e时,g′(x)<0,
g(x)为减函数;
x∈1e,+∞时,g′(x)>0,
g(x)为增函数.
所以当x=1e时,
g(x)min=a+(a+1)1eln1e=a(e−1)−1e.
由a(e−1)−1e<0,a+1>0,
得−11时,有g(x)<0恒成立,即存在x0∈(0,+∞),
使a+(a+1)x0lnx0<0,
综上,a的取值范围是−∞,1e−1.
第13页 共16页 ◎ 第14页 共16页
相关文档
- 人教版高中数学奇偶性2021-06-168页
- 2020_2021学年新教材高中数学第一2021-06-1638页
- 人教版高中数学必修二检测:第二章点2021-06-166页
- 高中数学人教a版选修2-2(课时训练):章2021-06-166页
- 人教A高中数学必修2全册复习2021-06-16102页
- 高中数学(人教版a版必修一)配套课时2021-06-169页
- 高中数学人教B版必修三第二章统计22021-06-166页
- 人教版高中数学必修二检测:第二章点2021-06-1610页
- 高中数学人教a版选修2-3练习:1-2-2-2021-06-164页
- 高中数学高考总复习等差数列习题及2021-06-1623页