人教A数学必修二 直线与圆的方程的应用 4页

‎4·2·3 直线与圆的方程的应用 一、知识导学：1、理解直线与圆、圆与圆的位置关系的几何性质；‎ ‎2、利用平面直角坐标系解决直线与圆、圆与圆的位置关系的有关问题；‎ ‎3、会用“数形结合”的数学思想解决问题，理解用坐标法解决几何问题的步骤。‎ 二、基础知识回顾：‎ ‎1、判断两条直线、的位置关系：通过解方程组确定交点坐标。‎ 已知两条直线：，：，‎ ‎（1）与相交；‎ ‎（2）与平行；‎ ‎（3）与重合。‎ ‎2、两点间、点到直线、两条平行线间的距离：‎ 距离及应用条件 公式及说明 两点间的距离 已知两点，‎ ‎1、公式：____________________；‎ ‎2、原点与任一点的距离 ‎=_______________。‎ 点到直线的距离 已知点，‎ 直线 ‎1、公式：____________________；‎ ‎2、当A=0或B=0时，公式仍成立；‎ ‎3、原点到直线的距离=____。‎ 两条平行线间的距离 ‎：，‎ ‎：，‎ ‎1、转化为点到直线的距离求解；‎ ‎2、公式：___________________。‎ ‎3、圆的标准方程：_________________________________。‎ ‎ 它表示以___________为圆心，以___________为半径的圆。‎ ‎4、圆的一般方程：。‎ 配方得__________________________________________。‎ ‎ （1）当时，表示以________为圆心，以________为半径的圆；‎ ‎（2）当时，表示一个点______________；‎ ‎（3）当时，它不表示任何图形。‎ ‎5、设直线：，圆H：，圆的半径为，‎ 圆心H到直线的距离为，其中：‎ ‎___________________，____________________。则：‎ 位置关系 公共点个数 与的关系 方程组解的个数 相交 相切 相离 ‎6、设两圆半径分别为，，连心线长为，则：‎ 位置 关系 公共点 个数 与，的关系 方程组解 的个数 公切线 条数 外离 外切 相交 内切 内含 当两圆外离时，它们的外公切线长为_____________________________；‎ ‎ 内公切线长为_____________________________。‎ 切线长定理：从圆外一点引圆的两条切线，他们的切线长_____________，‎ ‎ _________________________________平分两条切线的夹角。‎ 我们知道，圆内接四边形的_____________________相等；‎ 圆外切四边形的_____________________相等。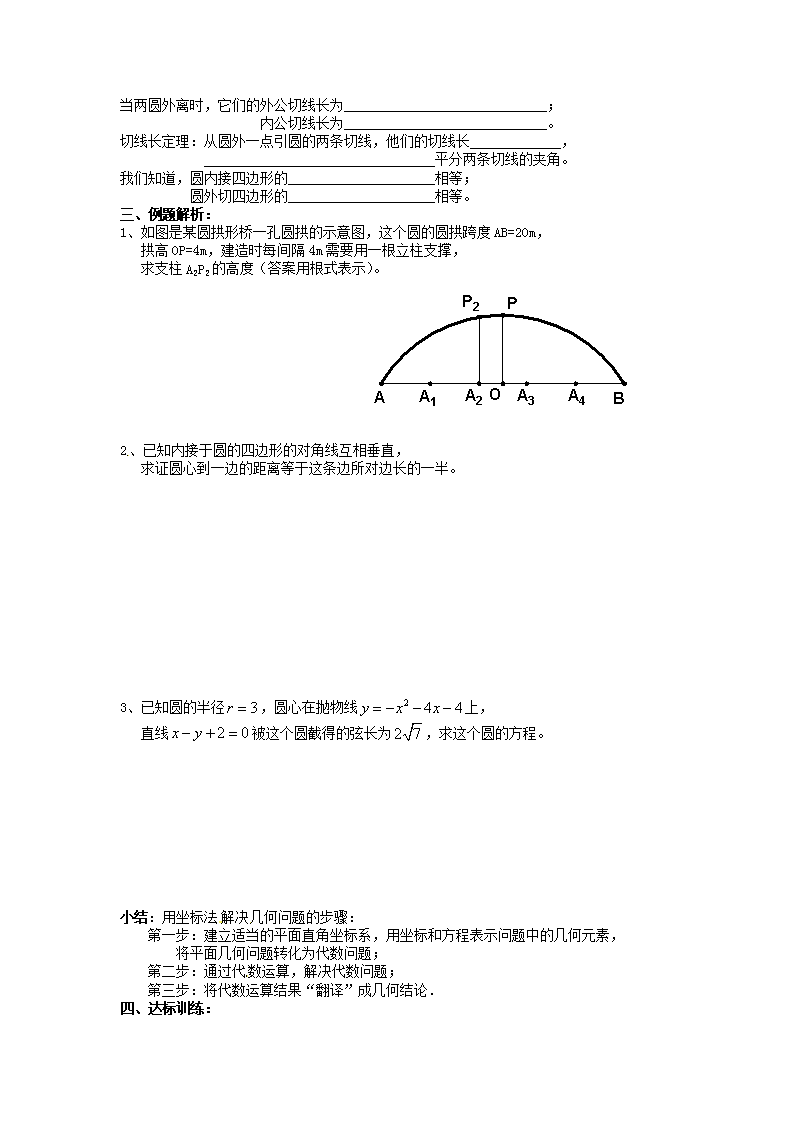‎ 三、例题解析：‎ ‎1、如图是某圆拱形桥一孔圆拱的示意图，这个圆的圆拱跨度AB=‎20m，‎ 拱高OP=‎4m，建造时每间隔‎4m需要用一根立柱支撑，‎ 求支柱A2P2的高度（答案用根式表示）。‎ ‎2、已知内接于圆的四边形的对角线互相垂直，‎ 求证圆心到一边的距离等于这条边所对边长的一半。‎ ‎3、已知圆的半径，圆心在抛物线上，‎ 直线被这个圆截得的弦长为，求这个圆的方程。‎ 小结：用坐标法解决几何问题的步骤：‎ 第一步：建立适当的平面直角坐标系，用坐标和方程表示问题中的几何元素，‎ 将平面几何问题转化为代数问题；‎ 第二步：通过代数运算，解决代数问题；‎ 第三步：将代数运算结果“翻译”成几何结论．‎ 四、达标训练：‎ ‎1、直线被圆所截得的弦长为____________。‎ ‎2、某圆拱桥的水面跨度是‎20m，圆拱高为‎4m，‎ 则这座圆拱桥的拱圆的方程为_________________________；‎ 现有一船，宽‎10m，水面以上高‎3m，这条船___（填能或不能）从桥下通过。‎ ‎3、过点A（-4，7）的圆的切线方程是____________________。‎ ‎4、已知直线和是某圆的两条切线，‎ 则该圆的面积是___________________________。‎ ‎5、圆与直线相交于A、B两点，‎ 圆心为P，若∠APB=90º，则的值为________________。‎ ‎6、圆关于点P（-2，1）对称的圆的方程为______。‎ ‎7、若M（3，0）是圆内一点，‎ 则过M点最长的弦所在直线的方程是_______________。‎ ‎8、若直线与圆相切，则的值为________。‎ ‎9、若点满足，‎ 则的最大值和最小值分别是______________和______________；‎ 的最大值和最小值分别是______________和______________；‎ 的最大值和最小值分别是______________和______________；‎ ‎10、自点P（-3，3）发出的光线经轴反射，其反射线所在的直线正好与 圆相切，则光线所在直线的方程为_________。‎ ‎11、直线将圆平分且不通过第四象限，‎ 则的斜率的取值范围是__________________________。‎ ‎12、已知圆，直线。若圆上恰有3个点 到直线的距离都等于1，则____________________。‎ ‎13、若圆上恰有相异两点到直线的距离等于1，‎ ‎ 则的取值范围是_____________________。‎ ‎14、等边△ABC中，点D，E分别在边BC，AC上，且，‎ ‎ ，AD，BE相交于点P，求证：AP⊥CP。‎ ‎15、已知点A（-2，-2），B（-2，6），C（4，-2），点在圆上运动，‎ ‎ 求的最大值和最小值。‎ ‎16、如图，圆内有一点，AB为过点且倾斜角为的弦。‎ ‎（1）当时，求AB的长；‎ ‎（2）当弦AB被点平分时，写出直线AB的方程。‎