2020_2021学年新教材高中数学第三章圆锥曲线的方程3 38页

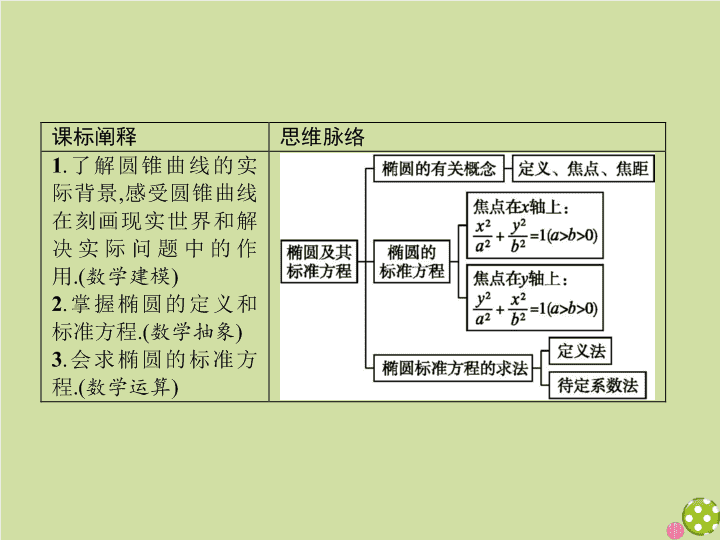
3.1.1 　椭圆及其标准方程 激趣诱思 知识点拨 《今日美国》 2018 年 12 月 9 日报道 ,“ 天文爱好者们即将看到一个惊喜 , 名为 ‘46 P/Wirtanen ’ 的彗星 , 即将成为 1950 年以来最 接近 地球的 10 颗彗星之一 . ‘ 46 P/Wirtanen ’ 会在美国时间 12 月 16 日最接近地球 . 届时 , 这颗彗星将 “ 仅 ” 距离地球 710 万英里 ( 从天文的角度来说 , 这已经很近了 ). 在此期间 , 这颗彗星应该肉眼可见 .” 天文学家是如何计算出彗星出现的准确时间呢 ? 原来 , 这颗彗星运行的轨道是一个椭圆 , 通过观察它运行中的一些有关数据 , 可以推算出它的运行轨道的方程 , 从而算出它运行的周期及轨道的周长 , 预测它接近地球或离去的时间 . 激趣诱思 知识点拨 一、椭圆的定义 1 . 定义 我们把平面内与两个定点 F 1 ,F 2 的距离的和等于常数 ( 大于 |F 1 F 2 |) 的点的轨迹叫做椭圆 . 这两个定点叫做椭圆的焦点 , 两焦点间的距离叫做椭圆的焦距 , 焦距的一半称为半焦距 . 2 . 定义的集合语言表述 集合 P={M||MF 1 |+|MF 2 |=2a,2a>|F 1 F 2 |}. 名师点析 在椭圆定义中 , 要求常数必须大于两定点 F 1 ,F 2 之间的距离 , 这是椭圆定义中非常重要的一个条件 , 可以验证 : 如果这个常数等于两定点 F 1 ,F 2 之间的距离 , 动点的轨迹将是一条线段 ; 如果这个常数小于两定点 F 1 ,F 2 之间的距离 , 动点的轨迹将不存在 . 因此在根据椭圆定义判断动点的轨迹时 , 务必注意这一隐含的条件 . 激趣诱思 知识点拨 微练习 下列说法中 , 正确的是 ( 　　 ) A. 到点 M(-3,0),N(3,0) 的距离之和等于 4 的点的轨迹是椭圆 B. 到点 M(0,-3),N(0,3) 的距离之和等于 6 的点的轨迹是椭圆 C. 到点 M(-3,0),N(3,0) 的距离之和等于 8 的点的轨迹是椭圆 D. 到点 M(0,-3),N(0,3) 的距离相等的点的轨迹是椭圆 答案 : C 激趣诱思 知识点拨 二、椭圆的标准 方程 0 0 0 激趣诱思 知识点拨 名师点析 1 . 椭圆的标准方程是指当椭圆在标准位置时的方程 , 所谓标准位置 , 就是指椭圆的中心在坐标原点 , 椭圆的对称轴为坐标轴 . 激趣诱思 知识点拨 (2) 已知 a=5,c=2, 焦点在 y 轴上 , 则椭圆的标准方程为 　　　　　　　 .   解析 : (1) 因为 10>6, 所以焦点在 x 轴上 , 且 a 2 =10,b 2 =6, 所以 c 2 =10-6=4,c=2, 故焦点坐标为 (2,0) 和 (-2,0). 激趣诱思 知识点拨 探究一 探究二 探究三 素养形成 当堂检测 求椭圆的标准方程 1 . 待定系数法 例 1 根据下列条件 , 求椭圆的标准方程 : (1) 两个焦点的坐标分别为 (-4,0) 和 (4,0), 且椭圆经过点 (5,0); (2) 焦点在 y 轴上 , 且经过两个点 (0,2) 和 (1,0); 思路分析 : (1) 设出焦点在 x 轴上的椭圆的标准方程 , 再根据条件求出 a,b 的值 , 即可求得方程 ;(2) 设出焦点在 y 轴上的椭圆的标准方程 , 再根据条件求出 a,b 的值 , 即可求得方程 ;(3) 焦点位置不确定 , 可以分两种情况分别求解 , 也可直接设所求椭圆方程为 mx 2 +ny 2 =1(m>0,n>0,m≠n). 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 椭圆方程的求法 1 . 利用待定系数法求椭圆标准方程的一般步骤如下 : (1) 先确定焦点位置 ;(2) 设出方程 ;(3) 寻求 a,b,c 的等量关系 ;(4) 求 a,b 的值 , 代入所设方程 . 2 . 当焦点位置不确定时 , 可设椭圆方程为 mx 2 +ny 2 =1(m≠n,m>0,n>0). 因为焦点位置包括焦点在 x 轴上 (mn) 两种情况 , 所以可以避免分类讨论 , 从而简化运算 . 探究一 探究二 探究三 素养形成 当堂检测 变式训练 1 根据下列条件 , 求椭圆的标准方程 . (2) 经过点 (2,-3) 且与椭圆 9x 2 +4y 2 =36 有共同的焦点 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 2 . 定义法 例 2 一个动圆与圆 Q 1 :(x+3) 2 +y 2 =1 外切 , 与圆 Q 2 :(x-3) 2 +y 2 =81 内切 , 试求这个动圆圆心的轨迹方程 . 思路分析 : 两圆相切时 , 圆心之间的距离与两圆的半径有关 , 由此可以找到动圆圆心满足的条件等式 . 解 : 两定圆的圆心和半径分别为 Q 1 (-3,0),r 1 =1;Q 2 (3,0),r 2 =9. 设动圆圆心为 M(x,y), 半径为 R, 由题意有 |MQ 1 |=1+R,|MQ 2 |=9-R, ∴ |MQ 1 |+|MQ 2 |=10>|Q 1 Q 2 |=6. 由椭圆的定义可知点 M 在以 Q 1 ,Q 2 为焦点的椭圆上 , 且 a=5,c=3, ∴ b 2 =a 2 -c 2 =25-9=16. 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 1 . 若动点轨迹满足椭圆的定义 , 则根据椭圆的定义来确定 a,b,c, 从而确定椭圆的标准方程 , 这种求轨迹方程的方法称为定义法 . 2 . 一般步骤 : (1) 将条件转化为到两定点的距离之和为定值 ( 该定值大于两定点之间的距离 ); (2) 判断椭圆的中心是否在原点、对称轴是否为坐标轴 ; (3) 确定椭圆的基本量 a,b,c, 从而确定椭圆的标准方程 . 探究一 探究二 探究三 素养形成 当堂检测 延伸探究 本题两个已知圆不变 , 若动圆与两个圆都内切 , 求动圆圆心的轨迹方程 . 解 : 设动圆圆心为 P(x,y), 半径为 r. 由圆 P 与圆 Q 1 内切 , 得 |PQ 1 |=r-1; 由圆 P 与圆 Q 2 内切 , 得 |PQ 2 |=9-r. 所以 |PQ 1 |+|PQ 2 |=8>6=|Q 1 Q 2 |. 所以 P 点轨迹是以 Q 1 ,Q 2 为焦点的椭圆 , 且 2a=8,2c=6. 即 a=4,c=3, 所以 b 2 =a 2 -c 2 =7. 探究一 探究二 探究三 素养形成 当堂检测 对椭圆标准方程的 理解 A. (-9,25) B. (-9,8) ∪ (8,25) C. (8,25) D. (8,+∞) (2) 若方程 x 2 -3my 2 =1 表示焦点在 x 轴上的椭圆 , 则实数 m 的取值范围是 　　　　　　　　　 .   探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 根据椭圆方程求参数的取值 范围 探究一 探究二 探究三 素养形成 当堂检测 答案 : (-4,0) ∪ (0,3 ) 探究一 探究二 探究三 素养形成 当堂检测 椭圆中的焦点三角形 问题 思路分析 : (1) 由 |PF 1 |+|PF 2 | 是定值 , 求 |PF 1 |·|PF 2 | 的最大值 , 可考虑用基本不等式 ;(2) 求焦点三角形的面积 , 可考虑用定义 |PF 1 |+|PF 2 |=2a 及余弦定理先求 |PF 1 |·|PF 2 |, 再考虑用三角形面积公式求面积 . 探究一 探究二 探究三 素养形成 当堂检测 当且仅当 |PF 1 |=|PF 2 |=10 时 , 等号成立 , 即 |PF 1 |·|PF 2 | 取到最大值 100. (2)c 2 =a 2 -b 2 =100-64=36,c=6, 则 F 1 (-6,0),F 2 (6,0). ∵ P 为椭圆上任一点 , ∴ |PF 1 |+|PF 2 |=2a=20. 在 △ PF 1 F 2 中 ,|F 1 F 2 |=2c=12, 探究一 探究二 探究三 素养形成 当堂检测 即 12 2 =|PF 1 | 2 +|PF 2 | 2 -|PF 1 |·|PF 2 |. ∵ |PF 1 | 2 +|PF 2 | 2 =(|PF 1 |+|PF 2 |) 2 -2|PF 1 |·|PF 2 |, ∴ 12 2 =(|PF 1 |+|PF 2 |) 2 -3|PF 1 |·|PF 2 |, ∴ 12 2 =20 2 -3|PF 1 |·|PF 2 |, 探究一 探究二 探究三 素养形成 当堂检测 反思感悟 1 . 焦点三角形的概念 如图 , 设 M 是椭圆上一点 ,F 1 ,F 2 为椭圆的焦点 , 当点 M,F 1 ,F 2 不在同一条直线上时 , 它们构成一个三角形 —— 焦点三角形 . 2 . 关于椭圆的焦点三角形问题 , 可结合椭圆的定义列出 |PF 1 |+|PF 2 |=2a, 利用这个关系式转化求解 . 因此回归定义是求解椭圆的焦点三角形问题的常用方法 . 在求解过程中要灵活运用勾股定理、正弦定理、余弦定理等 . 探究一 探究二 探究三 素养形成 当堂检测 3 . 焦点三角形的常用公式 (1) 焦点三角形的周长 L=2a+2c. (2) 在 △ MF 1 F 2 中 , 由余弦定理可 得 | F 1 F 2 | 2 =|MF 1 | 2 +|MF 2 | 2 -2|MF 1 ||MF 2 | cos θ . 探究一 探究二 探究三 素养形成 当堂检测 垂直于 x 轴 , 交椭圆于 A,B 两点 ,F 1 是椭圆的左焦点 . (1) 求 △ AF 1 B 的周长 . (2) 如果 AB 不垂直于 x 轴 , △ AF 1 B 的周长有变化吗 ? 为什么 ? 探究一 探究二 探究三 素养形成 当堂检测 故有 |AF 1 |+|AF 2 |=2a=10,|BF 1 |+|BF 2 |=2a=10,|AF 2 |+|BF 2 |=|AB|, ∴ △ AF 1 B 的周长 =|AF 1 |+|BF 1 |+|AB|=|AF 1 |+|BF 1 |+|AF 2 |+|BF 2 | =(| AF 1 |+|AF 2 |)+(|BF 1 |+|BF 2 |)=2a+2a=10+10=20, ∴ △ AF 1 B 的周长为 20. (2) 如果 AB 不垂直于 x 轴 , △ AF 1 B 的周长仍为 20 不变 . 理由 :|AF 1 |+|BF 1 |+|AB|=|AF 1 |+|BF 1 |+|AF 2 |+|BF 2 | =(| AF 1 |+|AF 2 |)+(|BF 1 |+|BF 2 |)=4a, 和 AB 与 x 轴是否垂直无关 . 探究一 探究二 探究三 素养形成 当堂检测 求与椭圆有关的轨迹问题 典例 已知 B,C 是两个定点 ,|BC|=8, 且 △ ABC 的周长等于 18. 求这个三角形的顶点 A 的轨迹方程 . 解 : 以过 B,C 两点的直线为 x 轴 , 线段 BC 的垂直平分线为 y 轴 , 建立平面直角坐标系 xOy, 如图所示 . 由 |BC|=8 可知点 B(-4,0),C(4,0). 由 |AB|+|AC|+|BC|=18, 得 |AB|+|AC|=10>8=|BC|, 因此 , 点 A 的轨迹是以 B,C 为焦点的椭圆 , 这个椭圆上的点与两焦点的距离之和 2a=10, 焦距 2c=8, 但点 A 不在 x 轴上 . 由 a=5,c=4, 得 b 2 =a 2 -c 2 =25-16=9. 探究一 探究二 探究三 素养形成 当堂检测 方法总结 求与椭圆有关的轨迹方程常用的方法 (1) 定义法 : 若动点的轨迹特点符合某一基本轨迹 ( 如椭圆、圆等 ) 的定义 , 则可用定义直接求解 . (2) 直接法 : 将动点满足的几何条件或者等量关系直接坐标化 , 列出等式后化简 , 得出动点的轨迹方程 . (3) 相关点法 : 根据相关点所满足的方程 , 通过转换求出动点轨迹的方程 . 探究一 探究二 探究三 素养形成 当堂检测 探究一 探究二 探究三 素养形成 当堂检测 1 . 已知 F 1 ,F 2 为两定点 ,|F 1 F 2 |=6, 动点 M 满足 |MF 1 |+|MF 2 |=16, 则动点 M 的轨迹是 ( 　　 ) A. 椭圆 B. 直线 C. 圆 D. 线段 解析 : 因为 |MF 1 |+|MF 2 |=16>|F 1 F 2 |, 所以动点 M 的轨迹是椭圆 . 答案 : A 探究一 探究二 探究三 素养形成 当堂检测 2 . 椭圆的两个焦点分别为 F 1 (-8,0),F 2 (8,0), 且椭圆上一点到两个焦点的距离之和为 20, 则此椭圆的标准方程为 ( 　　 ) 答案 : C 探究一 探究二 探究三 素养形成 当堂检测 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 答案 : B 探究一 探究二 探究三 素养形成 当堂检测 答案 : 6 探究一 探究二 探究三 素养形成 当堂检测 5 . 求以椭圆 9 x 2 + 5 y 2 = 45 的焦点为焦点 , 且经过点 M (2, ) 的椭圆的标准方程 .