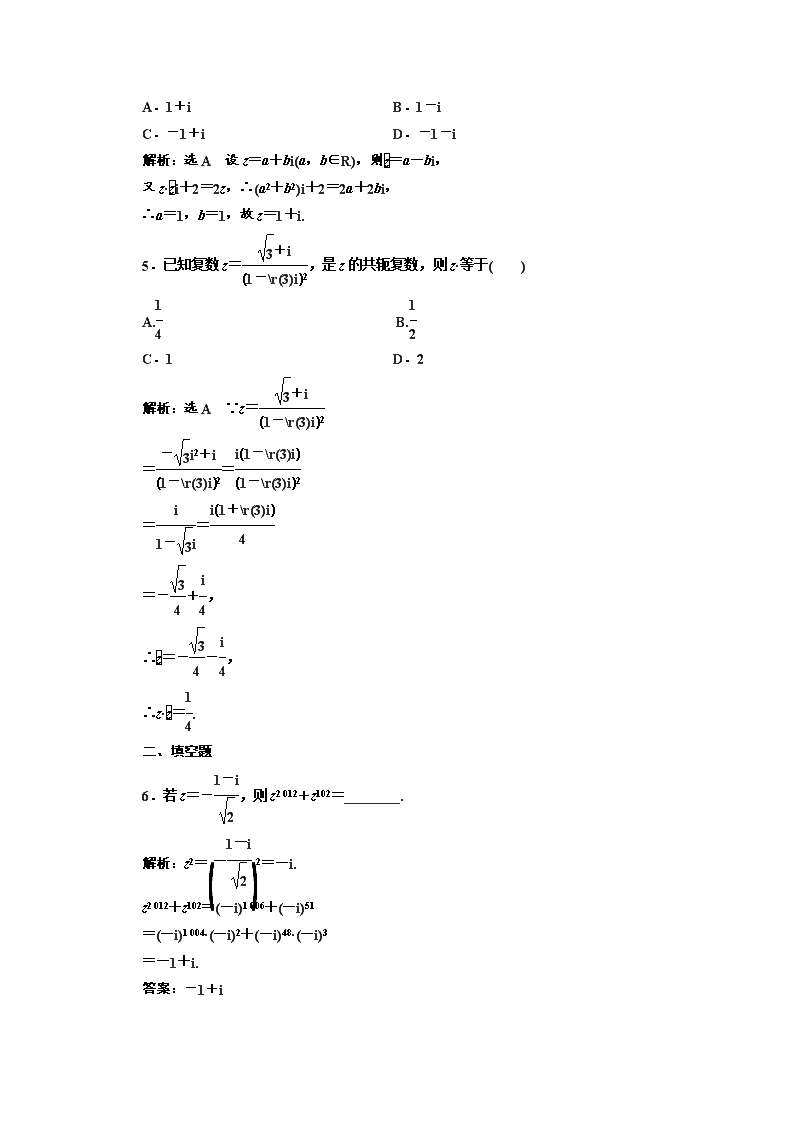高中数学人教a版选修1-2课时跟踪检测（十）复数代数形式的乘除运算word版含解析 4页

课时跟踪检测(十) 复数代数形式的乘除运算 一、选择题 1．(辽宁高考)设复数 z 满足(z－2i)(2－i)＝5，则 z＝( ) A．2＋3i B．2－3i C．3＋2i D．3－2i 解析：选 A z＝ 5 2－i ＋2i＝ 52＋i 2－i2＋i ＋2i＝2＋i＋2i ＝2＋3i. 2．已知复数 z＝1－i，则z2－2z z－1 ＝( ) A．2i B．－2i C．2 D．－2 解析：选 B 法一：因为 z＝1－i， 所以z2－2z z－1 ＝1－i2－21－i 1－i－1 ＝－2 －i ＝－2i. 法二：由已知得 z－1＝－i， 而z2－2z z－1 ＝z－12－1 z－1 ＝－i2－1 －i ＝2 i ＝－2i. 3．若 i 为虚数单位，如图中复平面内点 Z 表示复数 z，则表示复数 z 1＋i 的点是( ) A．E B．F C．G D．H 解析：选 D 由题图可得 z＝3＋i， 所以 z 1＋i ＝3＋i 1＋i ＝3＋i1－i 1＋i1－i ＝4－2i 2 ＝2－i， 则其在复平面上对应的点为 H(2，－1)． 4．(安徽高考)设 i 是虚数单位， 是复数 z 的共轭复数．若 z·i＋2＝2z，则 z＝( ) A．1＋i B．1－i C．－1＋i D．－1－i 解析：选 A 设 z＝a＋bi(a，b∈R)，则 z ＝a－bi， 又 z· z i＋2＝2z，∴(a2＋b2)i＋2＝2a＋2bi， ∴a＝1，b＝1，故 z＝1＋i. 5．已知复数 z＝ 3＋i 1－ 3i2 ，是 z 的共轭复数，则 z·等于( ) A.1 4 B.1 2 C．1 D．2 解析：选 A ∵z＝ 3＋i 1－ 3i2 ＝－ 3i2＋i 1－ 3i2 ＝i1－ 3i 1－ 3i2 ＝ i 1－ 3i ＝i1＋ 3i 4 ＝－ 3 4 ＋i 4 ， ∴ z ＝－ 3 4 －i 4 ， ∴z· z ＝1 4. 二、填空题 6．若 z＝－1－i 2 ，则 z2 012＋z102＝________. 解析：z2＝ －1－i 2 2＝－i. z2 012＋z102＝(－i)1 006＋(－i)51 ＝(－i)1 004·(－i)2＋(－i)48·(－i)3 ＝－1＋i. 答案：－1＋i 7．设 x，y 为实数，且 x 1－i ＋ y 1－2i ＝ 5 1－3i ，则 x＋y＝________. 解析： x 1－i ＋ y 1－2i ＝x1＋i 2 ＋y1＋2i 5 ＝ x 2 ＋y 5 ＋ x 2 ＋2y 5 i， 而 5 1－3i ＝51＋3i 10 ＝1 2 ＋3 2i， 所以x 2 ＋y 5 ＝1 2 且x 2 ＋2y 5 ＝3 2 ， 解得 x＝－1，y＝5，所以 x＋y＝4. 答案：4 8．设 z2＝z1－i1(其中 1 表示 z1 的共轭复数)，已知 z2 的实部是－1，则 z2 的虚部为________． 解析：设 z1＝a＋bi(a，b∈R)， 则 z2＝z1－i1＝a＋bi－i(a－bi)＝(a－b)－(a－b)i. 因为 z2 的实部是－1，即 a－b＝－1， 所以 z2 的虚部为 1. 答案：1 三、解答题 9．计算：(1)1＋2i2＋31－i 2＋i ； (2) 1－ 3i  3＋i2. 解：(1)1＋2i2＋31－i 2＋i ＝－3＋4i＋3－3i 2＋i ＝ i 2＋i ＝i2－i 5 ＝1 5 ＋2 5i. (2) 1－ 3i  3＋i2 ＝ 3＋i－i  3＋i2 ＝ －i 3＋i ＝－i 3－i 4 ＝－1 4 － 3 4 i. 10．已知 z1＝1－i，z2＝1－3i，z3＝1－2i，且x z1 －5 z2 ＝y z3 . (1)求实数 x，y 的值； (2)求 z1 · z2 . 解：(1)由已知x z1 －5 z2 ＝y z3 ， 得 x 1－i － 5 1－3i ＝ y 1－2i ， 即x－1 2 ＋x－3 2 i＝y 5 ＋2y 5 i. ∵x，y∈R， ∴ x－1 2 ＝y 5 ， x－3 2 ＝2y 5 ， 解得 x＝－1， y＝－5. (2)由(1)知 z1 ＝1＋i， z2 ＝1＋3i， 则 z1 · z2 ＝(1＋i)(1＋3i)＝1＋4i＋3i2＝－2＋4i.