高考数学一轮复习核心素养测评八2-5对数与对数函数文含解析北师大版 7页

核心素养测评八　对数与对数函数 ‎(25分钟　50分)‎ 一、选择题(每小题5分,共35分)‎ ‎1.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是 (　　)‎ ‎(参考数据:lg 3≈0.48)‎ A.1033 B‎.1053 ‎C.1073　 D.1093‎ ‎【解析】选D.设=x=,两边取对数,lg x=lg=lg 3361-lg1080=361×lg 3-80≈93.28,所以x=1093.28,即与最接近的是1093.‎ ‎2.(2020·上饶模拟)设函数f(x)=若f(a)>f(-a),则实数a的取值范围是 (　　)‎ A.(-1,0)∪(0,1) ‎ B.(-∞,-1)∪(1,+∞)‎ C.(-1,0)∪(1,+∞)‎ D.(-∞,-1)∪(0,1)‎ ‎【解析】选C.由题意得 或 解得a>1或-1b>c B.b>a>c C.a>c>b D.b>c>a ‎【解析】选D.由log2(log‎3a)=1,可得log‎3a=2,故a=32=9;由log3(log4b)=1,可得log4b=3,故b=43=64;由log4(log‎2c)=1,可得log‎2c=4,故c=24=16.所以b>c>a.‎ ‎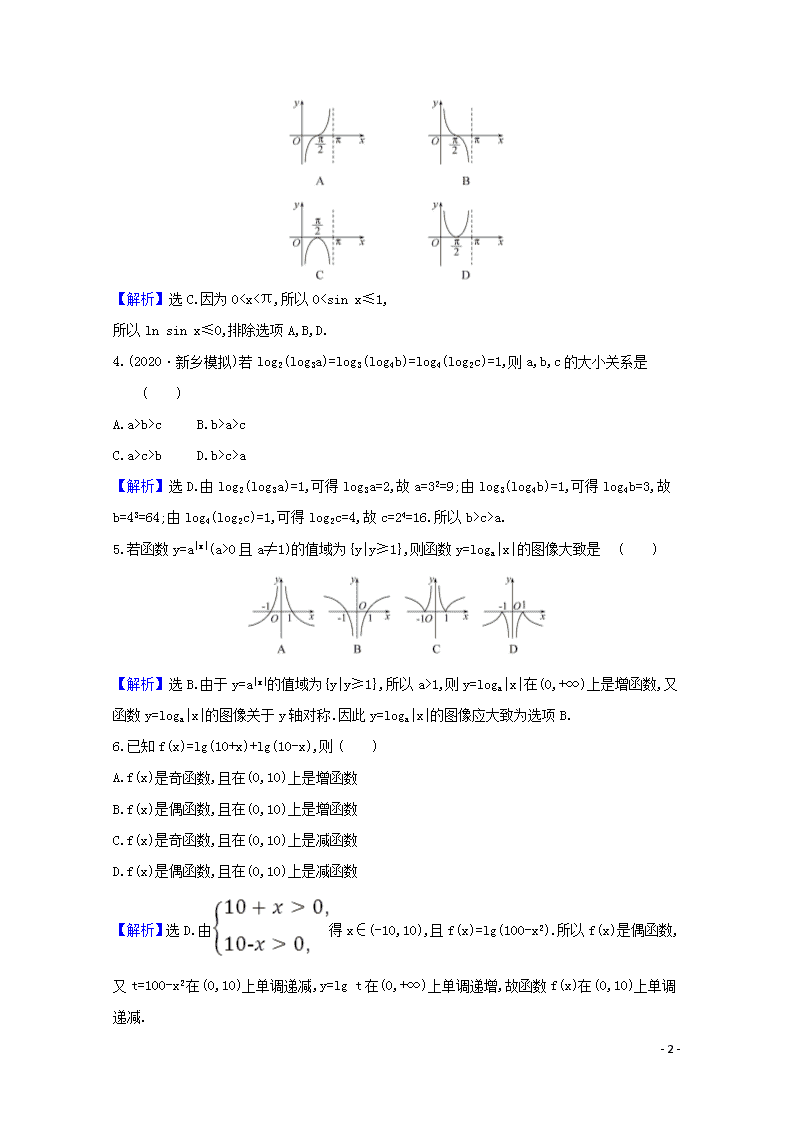5.若函数y=a|x|(a>0且a≠1)的值域为{y|y≥1},则函数y=loga|x|的图像大致是 (　　)‎ ‎【解析】选B.由于y=a|x|的值域为{y|y≥1},所以a>1,则y=loga|x|在(0,+∞)上是增函数,又函数y=loga|x|的图像关于y轴对称.因此y=loga|x|的图像应大致为选项B.‎ ‎6.已知f(x)=lg(10+x)+lg(10-x),则 (　　)‎ A.f(x)是奇函数,且在(0,10)上是增函数 B.f(x)是偶函数,且在(0,10)上是增函数 C.f(x)是奇函数,且在(0,10)上是减函数 D.f(x)是偶函数,且在(0,10)上是减函数 ‎【解析】选D.由得x∈(-10,10),且f(x)=lg(100-x2).所以f(x)是偶函数,‎ 又t=100-x2在(0,10)上单调递减,y=lg t在(0,+∞)上单调递增,故函数f(x)在(0,10)上单调递减.‎ - 7 -‎ ‎7.(2020·宁德模拟)已知函数f(x)=lg(|x|+1),记a=f(50.2),b=f(log0.23),c=f(1),则a,b,c的大小关系为 世纪金榜导学号(　　)‎ A.b50=1,00,解得00,a≠1)在区间内恒有f(x)>0,则f(x)的单调递增区间为　　　　. 世纪金榜导学号 ‎ ‎【解析】令M=x2+x,当x∈时,M∈(1,+∞),f(x)>0,所以a>1,所以函数y=logaM为增函数,又M=-,因此M的单调递增区间为.又x2+x>0,所以x>0或x<-,‎ 所以函数f(x)的单调递增区间为(0,+∞).‎ 答案:(0,+∞)‎ ‎(15分钟　35分)‎ ‎1.(5分)已知函数f(x)=|ln x|,若f(m)=f(n)(m>n>0),则+= (　　)‎ A.　　　 B‎.1　‎　　 C.2　　　 D.4‎ ‎【解析】选C.由f(m)=f(n),m>n>0,可知m>1>n>0,所以ln m=-ln n,则mn=1.‎ 所以+===2.‎ - 7 -‎ ‎2.(5分)(2020·威海模拟)已知函数f(x)=lnx+ln(a-x)的图像关于直线x=1对称,则函数f(x)的值域为 (　　)‎ A.(0,2)　　　　　　　　B.[0,+∞)‎ C.(-∞,2] D.(-∞,0]‎ ‎【解析】选D.因为函数f(x)=lnx+ln(a-x)的图像关于直线x=1对称,‎ 所以f(1-x)=f(1+x),即ln(1-x)+ln(a-1+x)=ln(1+x)+ln(a-1-x),‎ 所以(1-x)(a-1+x)=(1+x)(a-1-x),‎ 整理得(a-2)x=0恒成立,‎ 所以a=2,所以f(x)=lnx+ln(2-x),定义域为(0,2).‎ 又f(x)=lnx+ln(2-x)=ln(2x-x2),‎ 因为00,且a≠1)有最小值,则实数a的值等于　　　　. ‎ ‎【解析】令g(x)=x2-2x+a,则f(x)=loga[g(x)].‎ ‎①若a>1,由于函数f(x)有最小值,‎ 则g(x)应有最小值,‎ 而g(x)=x2-2x+a=(x-)2+a-6,‎ 当x=时,取最小值a-6,‎ 因此有解得a=9.‎ ‎②若00,a≠1),且f(1)=2. 世纪金榜导学号 ‎(1)求a的值及f(x)的定义域.‎ ‎(2)求f(x)在区间上的最大值.‎ ‎【解析】(1)因为f(1)=2,所以loga4=2(a>0,a≠1),‎ 所以a=2.由得-1