高中数学第三章指数函数和对数函数3_5对数函数问题导学案北师大版必修11 6页

§3.5 对数函数 问题导学 一、对数函数的概念及对数函数与指数函数的关系 活动与探究 1 (1)下列函数是对数函数的是( )． A．y＝log2(3x) B．y＝log2x3 C． 1 4 logy x D． 1 2 1logy x  (2)写出下列函数的反函数： ①y＝ 1 2 x；②y＝ln x. 迁移与应用 1．若对数函数 f(x)的图像经过点(16，－2)，那么 f(x)的解析式为__________． 2．若函数 y＝f(x)是函数 y＝ax(a＞0，且 a≠1)的反函数，其图像经过点( a，a)，则 f(x)等于( )． A．log2x B． 1 2 log x C．1 2x D．x2 (1)判断一个函数是否是对数函数，主要根据解析式的特征来判定，求对数函数解析式 时，主要利用待定系数法求出底数 a 的值． (2)函数 y＝logax 的反函数是 y＝ax(a＞0，且 a≠1)；函数 y＝ax 的反函数是 y＝logax(a ＞0，且 a≠1)． 二、求与对数函数有关的函数的定义域 活动与探究 2 求下列函数的定义域： (1)f(x)＝lg(4－x) x－3 ；(2)y＝ log0.1(4x－3). 迁移与应用 求下列函数的定义域： (1)y＝ 1 lg(x＋1)－3 ； (2)y＝ log3x－1. 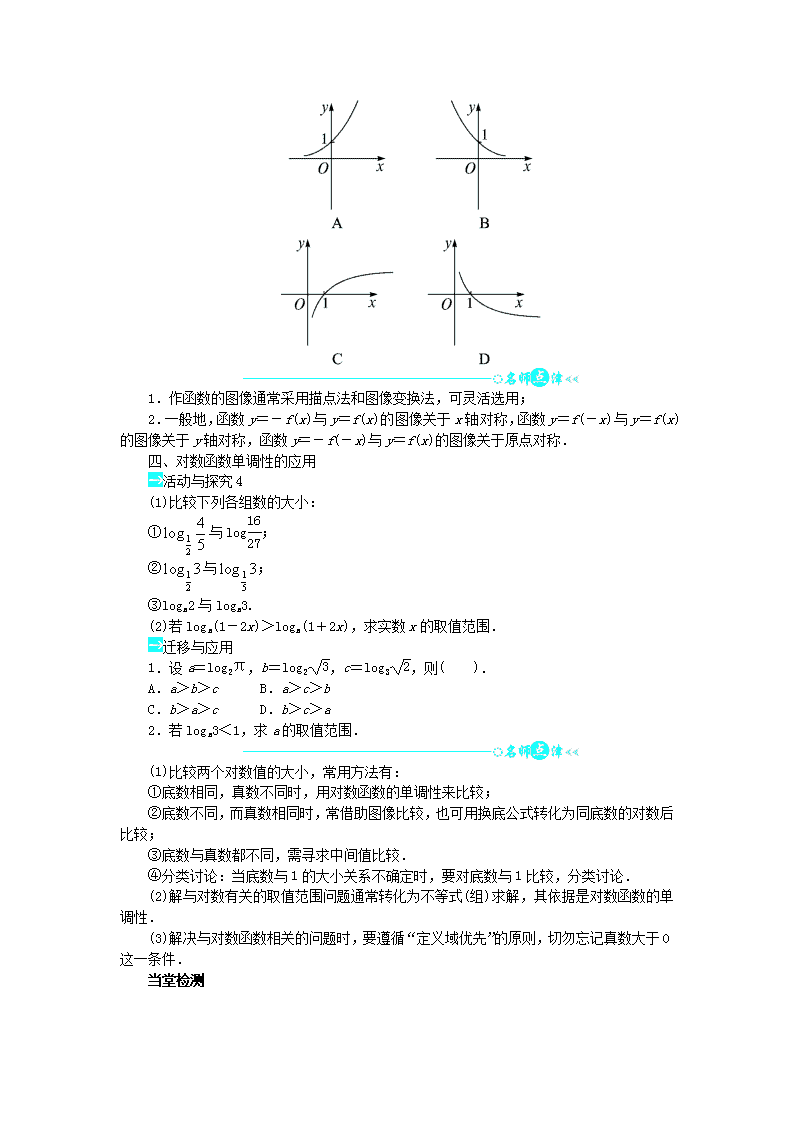求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还 要注意对数函数自身的要求：真数大于零． 三、对数函数的图像 活动与探究 3 作出函数 f(x)＝|log3x|的图像，并求出其值域和单调区间． 迁移与应用 函数 f(x)＝log4 1 x 的大致图像为( )． 1．作函数的图像通常采用描点法和图像变换法，可灵活选用； 2．一般地，函数 y＝－f(x)与 y＝f(x)的图像关于 x 轴对称，函数 y＝f(－x)与 y＝f(x) 的图像关于 y 轴对称，函数 y＝－f(－x)与 y＝f(x)的图像关于原点对称． 四、对数函数单调性的应用 活动与探究 4 (1)比较下列各组数的大小： ① 1 2 4log 5 与 log1 2 6 7 ； ② 1 2 log 3 与 1 5 log 3； ③loga2 与 loga3. (2)若 loga(1－2x)＞loga(1＋2x)，求实数 x 的取值范围． 迁移与应用 1．设 a＝log2π，b＝log2 3，c＝log3 2，则( )． A．a＞b＞c B．a＞c＞b C．b＞a＞c D．b＞c＞a 2．若 loga3＜1，求 a 的取值范围． (1)比较两个对数值的大小，常用方法有： ①底数相同，真数不同时，用对数函数的单调性来比较； ②底数不同，而真数相同时，常借助图像比较，也可用换底公式转化为同底数的对数后 比较； ③底数与真数都不同，需寻求中间值比较． ④分类讨论：当底数与 1 的大小关系不确定时，要对底数与 1 比较，分类讨论． (2)解与对数有关的取值范围问题通常转化为不等式(组)求解，其依据是对数函数的单 调性． (3)解决与对数函数相关的问题时，要遵循“定义域优先”的原则，切勿忘记真数大于 0 这一条件． 当堂检测 1．若函数 f(x)＝ 1 3 x 的反函数是 y＝g(x)，则 g(3)＝( )． A． 1 27 B．27 C．－1 D．1 2．若 log5x＜－1，则 x 的取值范围是( )． A．x＜1 5 B．0＜x＜1 5 C．x＞1 5 D．x＞5 3．下列不等式成立的是( )． A．log32＜log23＜log25 B．log32＜log25＜log23 C．log23＜log32＜log25 D．log23＜log25＜log32 4．函数 1 2 log (1 )y x  的定义域是__________． 5．画出下列函数的图像，并根据图像写出函数的定义域、值域以及单调区间： (1)y＝log3(x－2)； (2)y＝| 1 2 log x |. 提示：用最精炼的语言把你当堂掌握的核心知识的精 华部分和基本技能的要领部分写下来并进行识记。 答案： 课前预习导学 【预习导引】 1．y＝logax 底数 10 e 预习交流 1 提示：根据对数函数的定义，只有严格符合 y＝logax(a＞0，a≠1，x＞0) 形式的函数才是对数函数．例如 y＝log3x(x＞0)， 1 2 logy x (x＞0)是对数函数，而 y＝ 2log2x， 2 1 2 logy x 等都不是对数函数． 2．反函数 互换 y＝x 3．(1)描点法 先画函数 x＝log2y 的图像，再变换为 y＝log2x 的图像． (2)(1,0) y 轴右边 x 轴上方 x 轴下方 (0，＋∞) 4．(0，＋∞) (－∞，＋∞) (－∞，0) (0，＋∞) 预习交流 2 提示：不论 a(a＞0，且 a≠1)取何值，总有 loga1＝0，因此对数函数图像 过定点(1,0)，对于函数 y＝logaf(x)，若令 f(x)＝1 解得 x＝x0，那么其图像经过定点(x0,0)． 预习交流 3 提示：当 a＞1 时，a 值越大，图像越靠近 x 轴； 当 0＜a＜1 时，a 值越大，图像越远离 x 轴． 课堂合作探究 【问题导学】 活动与探究 1 思路分析：(1)根据对数函数的定义进行判断；(2)根据指数函数 y＝ax 与对数函数 y＝logax 的关系直接写出函数的反函数． (1)C 解析：由对数函数的定义知，只有函数 1 4 logy x 是对数函数，其余选项中的函 数均不是对数函数，故选 C. (2)解：①指数函数 y＝ 1 2 x，它的底数是1 2 ，它的反函数是对数函数 1 2 logy x . ②对数函数 y＝ln x，它的底数是 e，它的反函数是指数函数 y＝ex. 迁移与应用 1．   1 4 logf x x 解析：设 f(x)＝logax(a＞0，且 a≠1)，由已知得 loga16 ＝－2，因此 a－2＝16，解得 a＝1 4 ，故   1 4 logf x x . 2．B 解析：由题意，知 f(x)＝logax. ∵其图像过( a，a)， ∴a＝loga a.∴a＝1 2 .∴   1 2 logf x x . 活动与探究 2 思路分析：(1)x 取值需使分母不等于零且真数为正实数； (2)x 取值需使被开方数为非负数且真数为正实数． 解：(1)要使函数有意义，需有 4－x>0， x－3≠0， 解得 x＜4，且 x≠3， 所以函数的定义域为(－∞，3)∪(3,4)． (2)要使函数有意义，需有 4x－3>0， log0.1(4x－3)≥0， 即 4x－3>0， 4x－3≤1， 解得3 4 ＜x≤1. 所以函数的定义域为 3 4 ，1 . 迁移与应用 解：(1)∵由 lg(x＋1)－3≠0， x＋1>0， 得 x＋1≠103， x>－1， ∴x＞－1，且 x≠999， ∴函数的定义域为{x|x＞－1，且 x≠999}． (2)要使函数有意义，应有 log3x－1≥0， 即 log3x≥1，所以 x≥3， 即函数的定义域为{x|x≥3}． 活动与探究 3 思路分析：将函数 f(x)化为分段函数，结合对数函数及图像变换可作出 函数图像，然后通过图像求出值域和单调区间． 解：f(x)＝|log3x|＝ log3x，x≥1， －log3x，0log5 7 . ② 因 为 在 x∈(1 ， ＋ ∞) 上 ， 1 5 logy x 的 图 像 在 1 2 logy x 图 像 的 上 方 ， 所 以 1 1 2 5 log 30， 1＋2x>0， 1－2x>1＋2x， 解得－1 2 ＜x＜0； 当 0＜a＜1 时，依题意有 1－2x>0， 1＋2x>0， 1－2x<1＋2x， 解得 0＜x＜1 2 . 因此当 a＞1 时，x 的取值范围是 －1 2 ，0 ，当 0＜a＜1 时，x 的取值范围是 0，1 2 . 迁移与应用 1．A 解析：∵函数 y＝log2x 在(0，＋∞)上是增函数， ∴log2π＞log2 3，即 a＞b. 又∵b＝1 2 log23＞1 2 ，c＝1 2 log32＜1 2 ，∴b＞c. ∴a＞b＞c. 2．解：当 a＞1 时，原不等式可化为 loga3＜logaa， ∴a＞3. 当 0＜a＜1 时，原不等式可化为 loga3＜logaa， ∴a＜3. 又∵0＜a＜1，∴0＜a＜1. 综上知，所求 a 的取值范围是(0,1)∪(3，＋∞)． 【当堂检测】 1．C 解析：依题意 g(x)＝ 1 3 log x ，所以 g(3)＝ 1 3 log 3＝－1. 2．B 解析：由 log5x＜－1 可得 log5x＜log5 1 5 ，所以 0＜x＜1 5 . 3．A 解析：∵y＝log2x 在(0，＋∞)上是增函数， ∴log25＞log23＞log22＝1. 又 y＝log3x 在(0，＋∞)上为增函数， ∴log32＜log33＝1. ∴log32＜log23＜log25. 4．[0,1) 解析：∵由 1 2 log (1 )x ≥0， 得 0＜1－x≤1，∴0≤x＜1. 5．解：(1)函数 y＝log3(x－2)的图像可看作把函数 y＝log3x 的图像向右平移 2 个单位 长度得到的，如图①.其定义域为(2，＋∞)，值域为 R，在区间(2，＋∞)上是增函数． (2)y＝| 1 2 log x |＝ 1 2 2 log ,0 1, log , 1, x x x x     其图像如图②. 其定义域为(0，＋∞)，值域为[0，＋∞)，在(0,1]上是减少的，在(1，＋∞)上是增加 的．