- 152.50 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专练41 空间点、直线、平面之间的位置关系
命题范围:空间直线、平面的位置关系的定义及判断
[基础强化]
一、选择题
1.“点P在直线m上,m在平面α内”可表示为( )
A.P∈m,m∈α B.P∈m,m⊂α
C.P⊂m,m∈α D.P⊂m,m⊂α
2.在空间中,可以确定一个平面的条件是( )
A.两两相交的三条直线
B.三条直线,其中一条与另两条分别相交
C.三个点
D.三条直线,它们两两相交,但不交于同一点
3.四条线段顺次首尾相连,它们最多可确定的平面的个数为( )
A.4个 B.3个
C.2个 D.1个
4.若直线l1与l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1,l2都不相交
B.l与l1,l2都相交
C.l至多与l1,l2中的一条相交
D.l至少与l1,l2中的一条相交
5.若P是平面α外一点,则下列命题正确的是( )
A.过P只能作一条直线与平面α相交
B.过P可作无数条直线与平面α垂直
C.过P只能作一条直线与平面α平行
D.过P可作无数条直线与平面α平行
6.如图,α∩β=l,A、B∈α,C∈β,且C∉l, 直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
A.点A B.点B
C.点C但不过点M D.点C和点M
7.使直线a,b为异面直线的充分不必要条件是( )
A.a⊂平面α,b⊄α,a与b不平行
B.a⊂平面α,b⊄α,a与b不相交
C.a∥直线c,b∩c=A,b与a不相交
D.a⊂平面α,b⊂平面β,α∩β=l,a与b无公共点
8.[2019·全国卷Ⅲ]如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
9.[2019·全国卷Ⅱ]设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
10.在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )
A. B.
C. D.
二、填空题
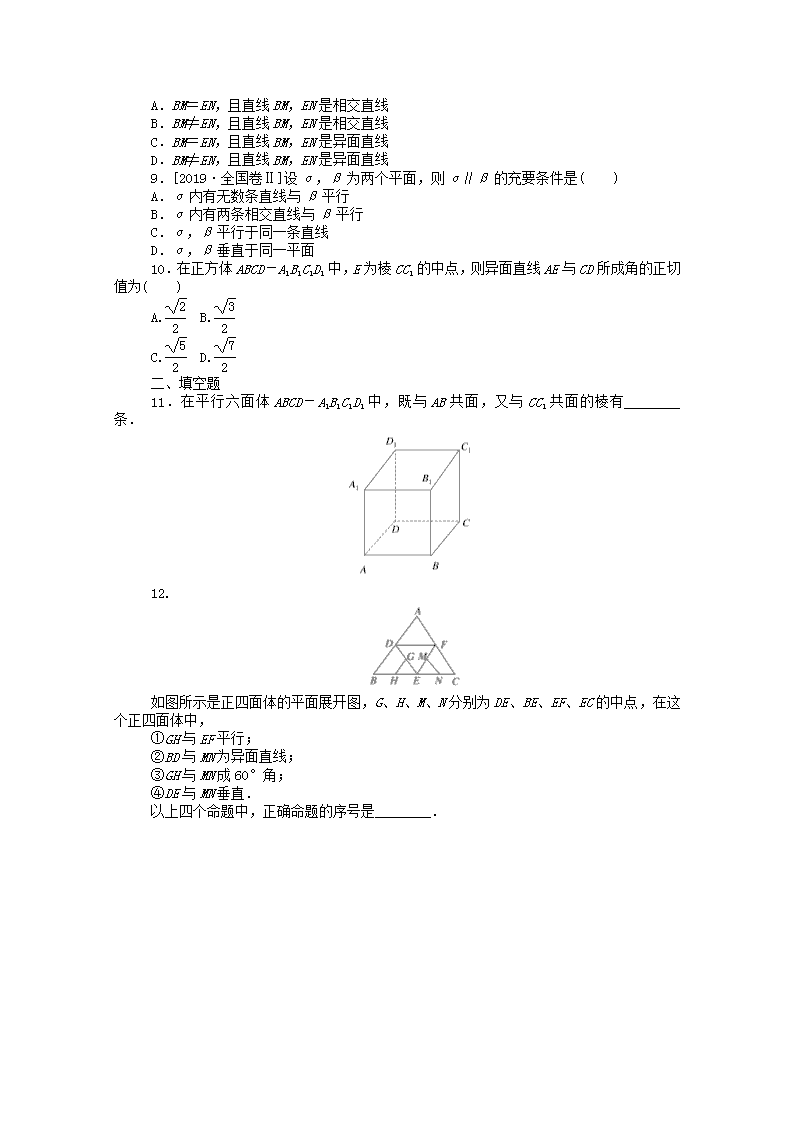
11.在平行六面体ABCD-A1B1C1D1中,既与AB共面,又与CC1共面的棱有________条.
12.
如图所示是正四面体的平面展开图,G、H、M、N分别为DE、BE、EF、EC的中点,在这个正四面体中,
①GH与EF平行;
②BD与MN为异面直线;
③GH与MN成60°角;
④DE与MN垂直.
以上四个命题中,正确命题的序号是________.
专练41 空间点、直线、平面之间的位置关系
1.B
2.D 当三条直线相交于同一点时,可以确定一个或三个平面,故A、B错;当三点共线时,不能确定一个平面,故C错,故选D.
3.A 首尾相连的四条线段每相邻两条确定一个平面,故最多可确定4个平面.
4.D 由直线l1和l2是异面直线可知l1与l2不平行,故l1,l2中至少有一条与l相交.
5.D 过平面α外一点P,可以作无数条直线与α相交,但垂直α的只有一条,故A、B、C均错,D正确.
6.D ∵A、B∈γ,M∈AB,∴M∈γ.又α∩β=l,M∈l,
∴M∈β.根据公理3可知,M在γ与β的交线上.同理可知,点C也在γ与β的交线上.
7.C 对A,a与b可能有交点,对于B、D,a与b可能平行,C显然正确.
8.B 本题主要考查空间线线位置关系,考查考生的空间想象能力,考查的核心素养是逻辑推理、直观想象、数学运算.
取CD的中点O,连接ON,EO,因为△ECD为正三角形,所以EO⊥CD,又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,所以EO⊥平面ABCD.设正方形ABCD的边长为2,则EO=,ON=1,所以EN2=EO2+ON2=4,得EN=2.过M作CD的垂线,垂足为P,连接BP,则MP=,CP=,所以BM2=MP2+BP2=()2+()2+22=7,得BM=,所以BM≠EN.连接BD,BE,因为四边形ABCD为正方形,所以N为BD的中点,即EN,MB均在平面BDE内,所以直线BM,EN是相交直线,选B.
9.B 本题主要考查直线与平面、平面与平面的位置关系,意在考查考生的空间想象能力、逻辑思维能力,考查的核心素养是数学抽象、逻辑推理、直观想象.
对于A,α内有无数条直线与β平行,当这无数条直线互相平行时,α与β可能相交,所以A不正确;对于B,根据两平面平行的判定定理与性质知,B正确;对于C,平行于同一条直线的两个平面可能相交,也可能平行,所以C不正确;对于D,垂直于同一平面的两个平面可能相交,也可能平行,如长方体的相邻两个侧面都垂直于底面,但它们是相交的,所以D不正确.综上可知选B.
10.
C 因为CD∥AB,所以∠BAE即为异面直线AE与CD所成的角.
设正方体的棱长为2,则BE=.
因为AB⊥平面BB1C1C,
所以AB⊥BE.
在Rt△ABE中,tan∠BAE==.
故选C.
11.5
解析:与AB和CC1都相交的棱为BC,与AB相交且与CC1平行的棱为AA1,BB1,与AB平行且与CC1相交的有CD,C1D1,故符合条件的棱有5条.
12.②③④
解析:还原成正四面体知GH与EF为异面直线,BD与MN为异面直线,GH与MN成60°角,DE与MN为异面直线,且所成的角为90°,即DE与MN垂直.
相关文档
- 【数学】2018届一轮复习苏教版诱导2021-06-163页
- 2020_2021学年新教材高中数学第三2021-06-1645页
- 江西省红色七校2020届高三第二次联2021-06-1624页
- 【数学】2020届一轮复习苏教版曲线2021-06-1617页
- 【数学】2020届一轮复习人教B版创2021-06-165页
- 【数学】2019届一轮复习北师大版分2021-06-167页
- 2021届高考数学一轮总复习第六章不2021-06-1629页
- 高中数学第三章指数函数和对数函数2021-06-166页
- 2021届高考数学一轮复习第八章立体2021-06-1638页
- 【数学】2021届新高考一轮复习北师2021-06-1611页